Bác An dự định mua một chiếc tủ lạnh loại 150 lít của hãng A, có sông suất 1Kwh/ngày với giá 5 000 000 đồng và dự định sẽ sử dụng nó trong vòng 10 năm.
a) Giả sử trong quá trình một tháng có 30 ngày và giá điện là 2000 đồng/1Kwh. Hãy tính số tiền điện phải trả hằng tháng cho chiếc tủ lạnh này.
b) Giả sử trong quá trình sử dụng, tủ lạnh không bị hỏng hóc cần sửa chữa gì. Khi đó chi phí sử dụng tủ lạnh bao gồm chi phí mua ban đầu và chi phí trả tiền điện hằng tháng. Lập công thức tính chi phí sử dụng chiếc tủ lạnh này sau x (tháng)
c) Sử dụng công thức đã lập ở câu b, hãy tính chi phí sử dụng của tủ lạnh sau 5 năm.
d) Bác An dùng phương pháp khấu hao đường thẳng để tính giá trị còn lại của chiếc tủ lạnh sau mỗi năm sử dụng. Hỏi sau 7 năm giá trị còn lại của chiếc tủ lạnh này là bao nhiêu?
e) Hãng B cùng một loại tủ lạnh 150 lít, công suất 1,25Kwh/ ngày với giá bán là 4 460 000 đồng.
- Lập công thức tính chi phí sử dụng chiếc tủ lạnh của hãng B sau x (tháng)
- Sau bao nhiêu tháng sử dụng thì chi phí sử dụng của hai loại tủ lạnh này là bằng nhau?
- Vẽ đồ thị của hai hàm số chi phí sử dụng của hai loại tủ lạnh trên cùng một hệ trục tọa độ. Từ đồ thị đã vẽ, theo em bác An nên mua tủ lạnh của hãng A hay hãng B để tiết kiệm chi phí sử dụng hơn? (Giả sử bác An sẽ sử dụng trong vòng 10 năm và chất lượng của hai loại tủ lạnh là tương đương).
a) Lấy 2000 . 30 ra số tiền điện phải trả trong 1 tháng
b) Lập công thức bằng chi phí ban đầu mua tủ lạnh và chi phí trả tiền điện mỗi tháng
c) Thay x = 12. 5 = 60 tháng vào công thức ở câu b
d) Sử dụng tủ lạnh trong 10 năm nên mỗi năm chiếc tủ lạnh sẽ giảm 5 000 000 : 10 = 500 000 (đồng)
tính chi phí còn lại của tủ lạnh sau 7 năm
e)
- Lập công thức tính chi phí sử dụng tủ lạnh của hãng B
- Chi phí sử dụng của hai loại tủ lạnh này là bằng nhau khi y bằng nhau
- Lấy hai điểm thuộc hàm số tìm được để vẽ đồ thị
a) Số tiền điện phải trả hàng tháng của chiếc tủ lạnh này là: 2000 . 30 = 60 000 (đồng)
b) Chi phí sử dụng của tủ lạnh sau x tháng là: y = 5 000 000 + 60 000. x
c) Chi phí sử dụng của lạnh sau 5 năm là: 5 000 000 + 60 000 . 60 = 8 600 000 (đồng)
d) Sử dụng tủ lạnh trong 10 năm nên mỗi năm chiếc tủ lạnh sẽ giảm 5 000 000 : 10 = 500 000 (đồng)
Giá trị còn lại của lạnh sau 7 năm là: 5 000 000 – 500 000 . 7 = 1 500 000 (đồng)
e)
- Công thức tính chi phí sử dụng của hãng B sau x tháng là:
y = 4 460 000 + 1, 25 . 2000. 30. x = 4 460 000 + 75 000. x (đồng)
- Chi phí sử dụng của hai loại tủ lạnh này là bằng nhau khi y bằng nhau nên ta có:
5 000 000 + 60 000 . x = 4 460 000 + 75 000 . x
Suy ra: x = 36
Vậy sau 36 tháng thì chi phí sử dụng của hai loại tủ lạnh là bằng nhau
- Để vẽ đồ thị hàm số y = 5 000 000 + 60 000. x ta lấy hai điểm A(0; 5 000 000), B(1; 5 060 000). Đường thẳng AB chính là đồ thị hàm số y = 5 000 000 + 60 000. x.
Để vẽ đồ thị hàm số y= 4 460 000 + 75 000. x ta lấy hai điểm C(0; 4 460 000), D(1; 4 535 000). Đường thẳng CD chính là đồ thị hàm số y = 4 460 000 + 75 000. x.
Ta có đồ thị hàm số như sau:
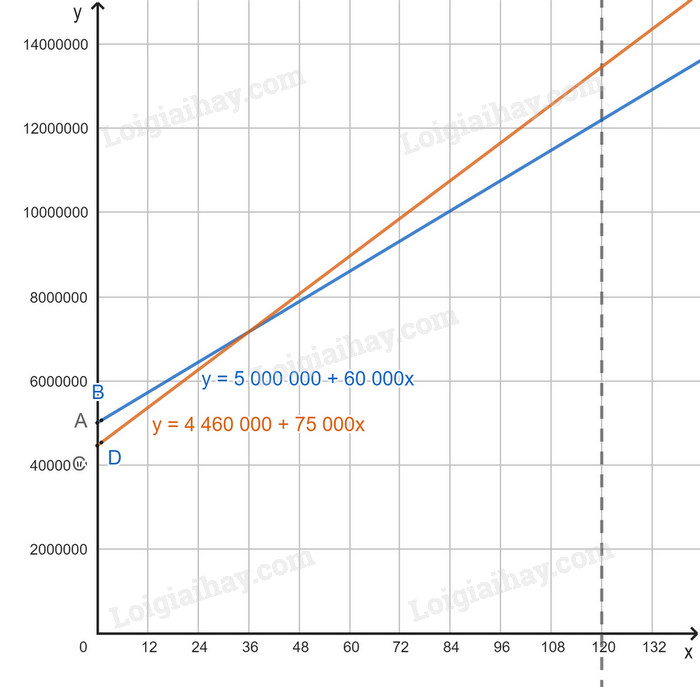
Quan sát đồ thị hàm số của hai hàm số trên, ta thấy tại thời điểm 10 năm (x = 10.12 = 120) thì hàm số y = 5 000 000 + 60 000.x nằm ở dưới.
Vậy nếu lựa chọn dịch vụ sử dụng trong 10 năm thì nên chọn tủ lạnh của hãng A tiết kiệm chi phí hơn tủ lạnh của hãng B

Các bài tập cùng chuyên đề
Giáo viên thực hiện nhiệm vụ sau:
Giả sử một gia đình có 5 triệu đồng để chi tiêu trong vòng 1 tuần. Yêu cầu mỗi học sinh lập kế hoạch chi tiêu cho gia đình đó theo mẫu bảng 2:
|
Khoản chi tiêu |
Số tiền (đồng) |
Tỉ lệ (%) |
|
Cho học tập của con, dịch vụ y tế và chăm sóc sức khỏe |
|
|
|
Cho các con nhu cầu thiết yếu |
|
|
|
Cho mua sắm cá nhân |
|
|
|
Cho tiết kiệm |
|
|
Mỗi nhóm học sinh tiến hành lập kế hoạch giả định về vay ngân hàng. Cụ thể như sau:
- Xác định số tiền vay nợ ngân hàng.
- Xác định nhu cầu cần vay
Sau đó, báo cáo kết quả kế hoạch giả định về vay nợ ngân hàng của nhóm theo mẫu sau:
1. Tên ngân hàng:
2. Tổng số tiền ngân hàng cho vay một lần:
3. Thời hạn cho vay (tính từ ngày nhận được khoản vay trên):
4. Lãi suất cho vay (Không thay đổi trong suất thời hạn hợp đồng):
5. Số tiền phải trả lãi mỗi tháng:
6. Số tiền phải trả nợ gốc mỗi tháng:
7. Tổng số tiền phải trả mỗi tháng cho ngân hàng:
Xây dựng công thức của hàm chi phí
Chi phí sử dụng truyền hình cáp của hai công ty dịch vụ truyền hình A và B như sau:

a) Viết công thức tính chi phí sử dụng truyền hình cáp y (nghìn đồng) của mỗi công ty A và B theo số tháng sử dụng là x (tháng)
b) Tính chi phí sử dụng truyền hình cáp trong 18 tháng của mỗi công ty A và B.
c) Với bao nhiêu tháng sử dụng thì chi phí sử dụng truyền hình cáp của hai công ty này là như nhau?
d) Vẽ đồ thị của hai hàm số nhận được ở câu a trên cùng một hệ trục tọa độ. Từ đó hãy cho biết nếu một gia đình dự định dùng một dịch vụ truyền hình cáp trong 3 năm thì nên chọn dịch vụ của công ty A hay công ty B để tiết kiệm chi phí hơn (giả sử chất lượng dịch vụ truyền hình cáp của hai công ty này là như nhau)
Giả sử rằng một hãng taxi vừa mua một số ô tô để chạy dịch vụ với chi phí là 480 triệu đồng một chiếc. Công ty chọn khấu hao theo đường thẳng trong vòng 8 năm. Điều này có nghĩa là mỗi chiếc xe sẽ giám giá 480 : 8 = 60 triệu đồng mỗi năm.
a) Tính giá trị sổ sách y(triệu đồng) của mỗi chiếc ô tô dưới dạng một hàm số bậc nhất của thời gian sử dụng x (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất.
c) Giá trị sổ sách của mỗi chiếc ô tô sau 3 năm sử dụng là bao nhiêu?
d) Sau bao lâu thì giá trị sổ sách của mỗi chiếc ô tô còn lại là 150 triệu đồng?







Danh sách bình luận