Cặp tam giác vuông nào đồng dạng với nhau trong hình 9.55
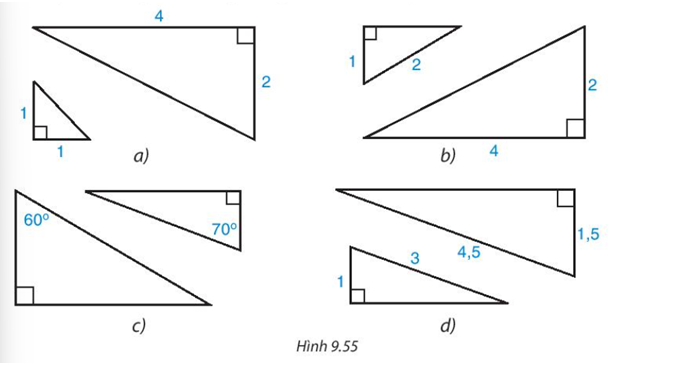
Các trường hợp đồng dạng của tam giác vuông
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

Các bài tập cùng chuyên đề
Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:

Điều kiện nào dưới đây chứng tỏ hai tam giác vuông đồng dạng
a) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia
b) Cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia
c) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia
d) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia
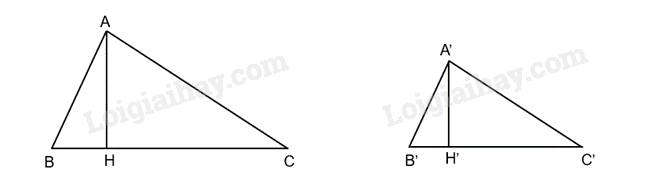
Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC. Chứng minh rằng:
a) \(\frac{{A'H'}}{{AH}} = k\)
b) Diện tích tam giác A'B'C' bằng \(k^2\) lần diện tích tam giác ABC
Hãy tìm cặp tam giác vuông đồng dạng trong Hình 8.

Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3m và đặt cách xa tòa nhà 27m. Sau khi người ấy lùi xa cái cọc 1,2m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng năm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m.
Cho tam giác \(ABC\) vuông tại \(A\left( {AB < AC} \right)\). Kẻ đường cao \(AH\left( {H \in BC} \right)\).
a) Chứng minh rằng \(\Delta ABH\backsim\Delta CBA\), suy ra \(A{B^2} = BH.BC\).
b) Vẽ \(HE\) vuông góc với \(AB\) tại \(E\), vẽ \(HF\) vuông góc với \(AC\) tại \(F\). Chứng minh rằng \(AE.AB = AF.AC\).
c) Chứng minh rằng \(\Delta AFE\backsim\Delta ABC\).
d) Qua \(A\) vẽ đường thẳng song song với \(BC\) cắt đường thẳng \(HF\) tại \(I\). Vẽ \(IN\) vuông góc với \(BC\) tại \(N\). Chứng minh rằng \(\Delta HNF\backsim\Delta HIC\).
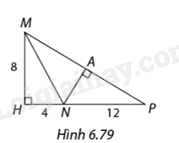
Chứng minh rằng trong Hình 6.79, \(\Delta HMN\) đồng dạng với \(\Delta HPM\) và \(\Delta APN\).
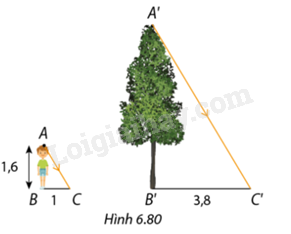
Vào một thời điểm trong ngày, bóng của bạn An trên mặt đất là \(BC = 1m\), còn bóng cây \(A'B'\) là \(B'C' = 3,8m\) (Hình 6.80). Biết An cao 1,6m, hỏi cây cao bao nhiêu mét? Làm tròn kết quả đến hàng phần mười.
Những điều kiện nào dưới đây kéo theo hai tam giác vuông đồng dạng.
(1) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia.
(2) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia.
(3) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.
(4) Một góc nhọn của tam giác này phụ với một góc nhọn của tam giác kia.
(5) Một cạnh huyền của tam giác này bằng một cạnh huyền của tam giác kia.
(6) Một cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với một cạnh góc vuông và cạnh huyền của tam giác kia.
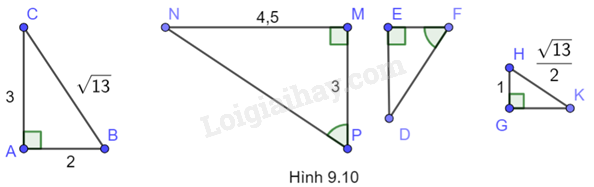
Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng?
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là điểm bất kì trên cạnh AC. Kẻ \(MD \bot BC\left( {D \in BC} \right)\).
a) Chứng minh rằng $\Delta DMC\backsim \Delta ABC$.
b) Gọi E là giao điểm của đường thẳng AB và đường thẳng MD. Chứng minh rằng \(DB.DC = DE.DM\)
c) Đường thẳng BM cắt EC tại K. Chứng minh rằng \(\widehat {EKA} = \widehat {EBC}\).
Cho tam giác nhọn ABC, các đường cao AM, BN, CQ cắt nhau tại H. Chứng minh rằng:
a) Chứng minh rằng $\Delta ANQ\backsim \Delta ABC$.
b) Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng \(FB.FC = FQ.FN\).
c) Trên đoạn HB lấy điểm I sao cho \(\widehat {AIC} = {90^0}\). Chứng minh rằng \(A{I^2} = AN.AC\).
d) Trên đoạn HC lấy điểm K sao cho \(\widehat {AKB} = {90^0}\). Chứng minh rằng \(\Delta AIK\) cân.
Cho tam giác ABC vuông tại A và đường cao AH.
a) Chứng minh rằng \(A{B^2} = BH.BC\).
b) Chứng minh rằng \(A{H^2} = BH.CH\).
c) Trên tia đối của tia AC lấy điểm D \(\left( {AD < AC} \right)\). Đường thẳng qua H và song song với AC cắt AB, BD lần lượt tại M, N. Chứng minh rằng \(\frac{{MN}}{{MH}} = \frac{{AD}}{{AC}}\).
d) Vẽ AE vuông góc với BD tại E. Chứng minh rằng \(\widehat {BEH} = \widehat {BAH}\).
Cho tam giác \(ABC\) có ba góc nhọn, các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Chứng minh:
a) \(\Delta EBH\backsim \Delta DCH,\Delta ADE\backsim \Delta ABC\);
b) \(DB\) là tia phân giác của góc \(EDI\), với \(I\) là giao điểm của \(AH\) và \(BC\).
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều kiện nào dưới đây không suy ra $\Delta ABC\backsim \Delta DEF$?
A. $\widehat{B}=\widehat{E}$.
B. $\frac{AB}{DE}=\frac{AC}{DF}$.
C. $\frac{AB}{DE}=\frac{BC}{EF}$.
D. $\widehat{C}=\widehat{E}$.
Điều kiện nào dưới đây chứng tỏ hai tam giác vuông đồng dạng
a) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia
b) Cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia
c) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia
d) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia
Cặp tam giác vuông nào đồng dạng với nhau trong hình 9.14?

Hình 9.14
Cho hình vuông ABCD có cạnh bằng 4cm và M, N lần lượt là trung điểm của AB, BC.
Gọi O là giao điểm của CM và DN (H.9.17). Tính độ dài đoạn thẳng OM.

Trong hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng
a) ΔAEH ∽ ΔAHB
b) ΔAFH ∽ ΔAHC
c) ΔAFE ∽ ΔABC
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF
A. \(\hat{B}=\hat{E}\).
B. \(\hat{C}=\hat{F}\).
C. \(\hat{B}+\hat{C}=\hat{E}+\hat{F}\).
D. \(\hat{B}-\hat{C}=\hat{E}-\hat{F}\).
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC. Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
Cho \(\Delta ABC\) có AB = 18cm, AC = 24cm, BC = 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt AC, AB lần lượt tại D, E.
a) Chứng minh rằng $\Delta ABC\backsim \Delta MDC$.
b) Tính độ dài các cạnh của \(\Delta MDC\).
c) Tính độ dài BE, EC.
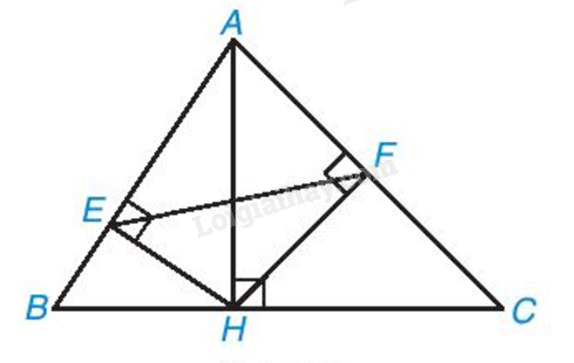
Cho tam giác ABC có đường cao AH. Lấy E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:
a) \(AE.AB = AF.AC\)
b) $\Delta ADE\backsim \Delta AHC$ và $\Delta ANF\backsim \Delta AMB$ ($\Delta ANF\backsim \Delta AMB$ không chứng minh được vì đề bài không cho vị trí của điểm N).
Cho tam giác ABC vuông tại A (AB > AC), đường cao AH. Từ B kẻ tia \(Bx \bot AB\), tia Bx cắt AH tại K.
a) Tứ giác ABKC là hình gì? Tại sao?
b) Chứng minh $\Delta ABK\backsim \Delta CHA$. Từ đó suy ra \(AB.AC = AK.CH\).
c) Chứng minh \(A{H^2} = HB.HC\).
d) Giả sử \(BH = 9cm,HC = 16cm\). Tính AB, AH.







Danh sách bình luận