Ở một bể chứa nước có chứa 1000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào bể nước với tốc độ là 25 lít/phút.
a) Chứng minh rằng nồng độ muối của nước trong bể sau t phút kể từ khi bắt đầu bơm là: \(C(t) = \frac{{30t}}{{40 + t}}.\)
b) Khảo sát sự biến thiên của hàm số \(y = C(t)\) sau 10 tiếng kể từ lúc bắt đầu bơm, từ đó nhận xét về nồng độ muối trong bể khi thời gian t càng lớn.
a)
Tính lượng nước biển bơm vào sau 𝑡 phút.
Tính tổng lượng nước trong bể sau 𝑡 phút.
Tính lượng muối bơm vào bể sau 𝑡 phút.
Tính nồng độ muối 𝐶(𝑡).
b)
Tính giới hạn của C(t) khi \(t \to \infty \).
Tính đạo hàm của C(t).
Xét dấu của đạo hàm C’(t).
Từ dấu của đạo hàm và giới hạn khi \(t \to \infty \) kết luận về sự biến thiên và giá trị tiệm cận của hàm số.
a)
Lượng nước biển bơm vào sau \(t\) phút: \(V = 25t\) lít.
Tổng lượng nước trong bể sau \(t\) phút: \(1000 + 25t\) lít.
Lượng muối bơm vào bể sau \(t\) phút: \(30.25t = 750t\) gam.
Nồng độ muối \(C(t) = \frac{{750t}}{{1000 + 25t}} = \frac{{750t}}{{25(40 + t)}} = \frac{{30t}}{{40 + t}}.\)
b)
Vì t là thời gian nên tập xác định của hàm số \({\rm{y}} = C(t)\) là t > 0.
Giới hạn của \(C(t)\) khi t càng lớn (tiến tới vô cực): \(\mathop {\lim }\limits_{t \to \infty } \frac{{30t}}{{40 + t}} = 30.\)
Đạo hàm của \(C(t)\) : \({C^\prime }(t) = \frac{{30.(40 + t) - 30t.1}}{{{{(40 + t)}^2}}} = \frac{{1200 + 30t - 30t}}{{{{(40 + t)}^2}}} = \frac{{1200}}{{{{(40 + t)}^2}}}.\)
Nhận thấy \({C^\prime }(t) > 0\forall t > 0.\)
Vậy nồng độ muối trong bể tăng dần khi thời gian \(t\) càng lớn.
Khi đó, nồng độ muối trong bể tiệm cận 30 gam/lít.

Các bài tập cùng chuyên đề
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{2x + 1}}{{x + 1}}\);
b) \(y = \frac{{x + 3}}{{1 - x}}\).
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{2{x^2} - x + 4}}{{x - 1}}\);
b) \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}}\).
Trong Vật lí, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\) thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
Giả sử một điện trở \(8\Omega \) được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là \(x\left( \Omega \right)\) thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số \(y = R\left( x \right),x > 0\) và dựa vào đồ thị đã vẽ, hãy cho biết:
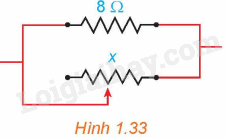
a) Điện trở tương đương của mạch thay đổi thế nào khi x tăng.
b) Tại sao điện trở tương đương của mạch không bao giờ vượt quá \(8\Omega \).
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{ - {x^2} + 3x - 1}}{{x - 2}}\).
Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hòa tan).
a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.
b) Coi nồng độ chất khử trùng là hàm số f(t) với \(t \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Hãy giải thích tại sao nồng độ chất khử tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.
Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức \(p = \frac{{354}}{{1 + 0,01x}},x \ge 0\), trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.
a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(x = x\left( p \right)\). Từ đồ thị đã vẽ, hãy cho biết:
- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;
- Ý nghĩa thực tiễn của giới hạn \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right)\).
Đường cong nào sau đây là đồ thị của hàm số \(y = \frac{{1 - x}}{{x + 1}}\) ?
Đường cong ở hình 30 là đồ thị của hàm số:


Khảo sát sự biến thiên của các hàm số sau:
a, \(y = \frac{{x - 1}}{{x + 1}}\)
b,\(y = \frac{{ - 2x}}{{x + 1}}\)
c,\(y=\frac{{{x^2} - 3x + 6}}{{x - 1}}\)
d,\(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)
e,\(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\)
g,\(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)
Đường cong của hình 33 là đồ thị của hàm số nào sau đây

A. \(y = \frac{{x + 1}}{{x - 1}}\)
B. \(y = \frac{{ - x + 1}}{{x + 1}}\)
C. \(y = \frac{{x - 1}}{{x + 1}}\)
D. \(y = \frac{{ - x}}{{x + 1}}\)
Các dồ thị hàm số ở hình 34a, hình 34b đều có đường tiệm cận đứng và đường tiệm cận ngang ( hoặc tiệm cận xiên). Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

a, \(y = \frac{{2x + 3}}{{x + 1}}\)
\(b,\;y = \frac{{2x - 5}}{{x - 1}}\)
\(c,\;y = \frac{{2{x^2} + 3x}}{{x + 1}}\)
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{2x}}{{3x - 1}}\)
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x - \frac{1}{x}\)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
c) \(y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\)
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = 3 + \frac{1}{x}\)
b) \(y = \frac{{x - 3}}{{1 - x}}\)
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{{x^2} - 2x + 2}}{{x - 1}}\)
b) \(y = 2x - \frac{1}{{1 - 2x}}\)
Cho hàm số: \(y = \frac{{ - {x^2} + 3x + 1}}{{x + 2}}\).
a) Khảo sát và vẽ đồ thị của hàm số đã cho.
b) Tìm toạ độ trung điểm đoạn nối hai điểm cực trị của đồ thị hàm số. Có nhận xét gì về điểm này?
Cho hàm số \(y = \frac{{2x + 1}}{{x - 1}}\)
a) Khảo sát và vẽ đồ thị của hàm số.
b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.
Cho hàm số \(y = \frac{{{x^2} + 4x - 1}}{{x - 1}}\)
a) Khảo sát và vẽ đồ thị của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [2; 4].
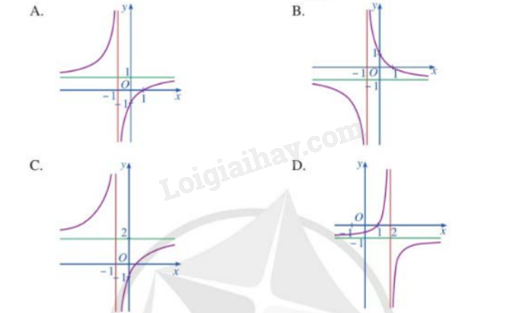
Đường cong dưới đây là đồ thị hàm số nào?
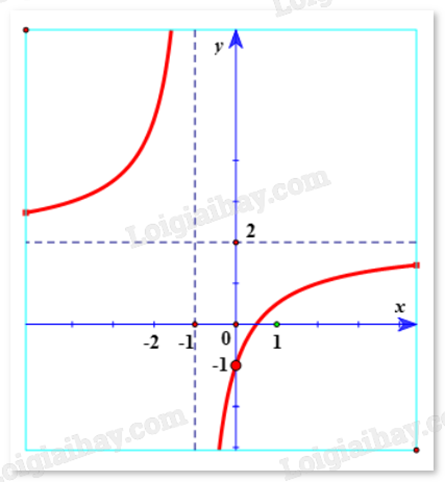
-
A.
\(y = \frac{{2x - 1}}{{x + 1}}\)
-
B.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
C.
\(y = \frac{{2x + 1}}{{x + 1}}\)
-
D.
\(y = \frac{{1 - 2x}}{{x - 1}}\)
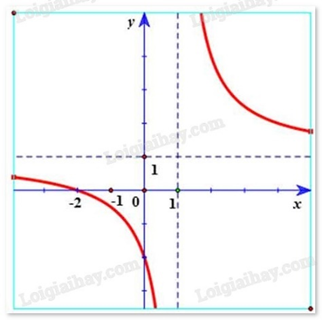
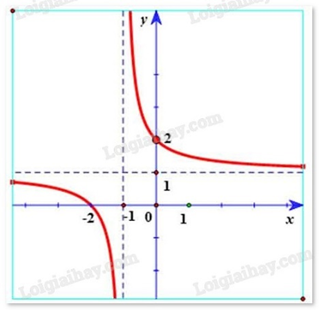
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
-
A.
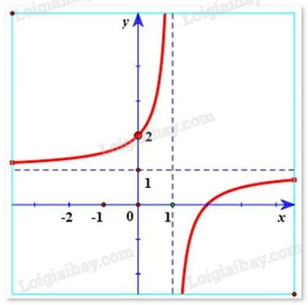
-
B.
-
C.
-
D.
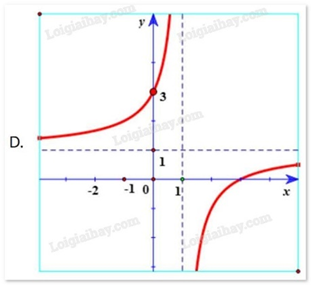
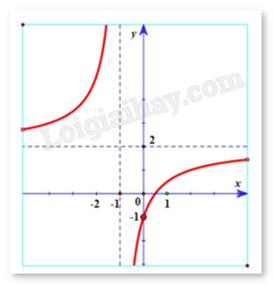
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
-
A.
\(y = \frac{{2x - 1}}{{x + 1}}\)
-
B.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
C.
\(y = \frac{{2x + 1}}{{x + 1}}\)
-
D.
\(y = \frac{{1 - 2x}}{{x - 1}}\)
Cho hàm số có bảng biến thiên như hình vẽ sau.
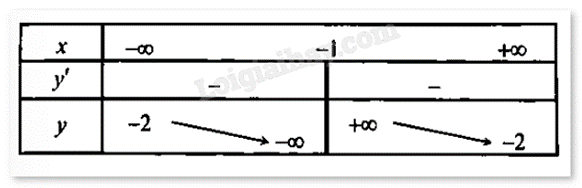
Xác định công thức của hàm số.
-
A.
\(y = \frac{{x - 4}}{{2x + 2}}\)
-
B.
\(y = \frac{{ - 2x - 4}}{{x + 1}}\)
-
C.
\(y = \frac{{ - 2x + 3}}{{x + 1}}\)
-
D.
\(y = \frac{{2 - x}}{{x + 1}}\)
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?
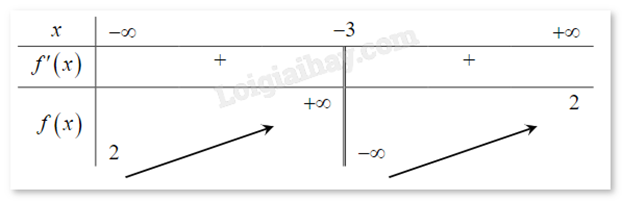
-
A.
\(y = \frac{{2x + 1}}{{x - 3}}\)
-
B.
\(y = \frac{{2 - x}}{{x + 3}}\)
-
C.
\(y = \frac{{2x + 7}}{{x + 3}}\)
-
D.
\(y = \frac{{2x - 1}}{{x + 3}}\)
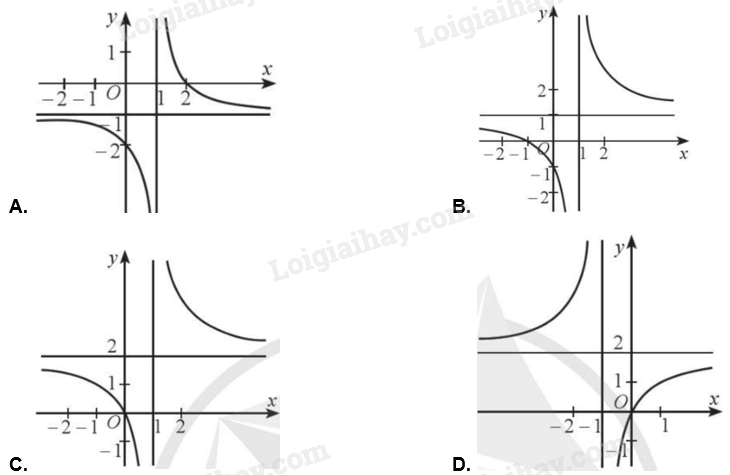
Đồ thị hàm số \(y = \frac{{2{\rm{x}}}}{{x + 1}}\) là đường cong nào trong các đường cong sau?
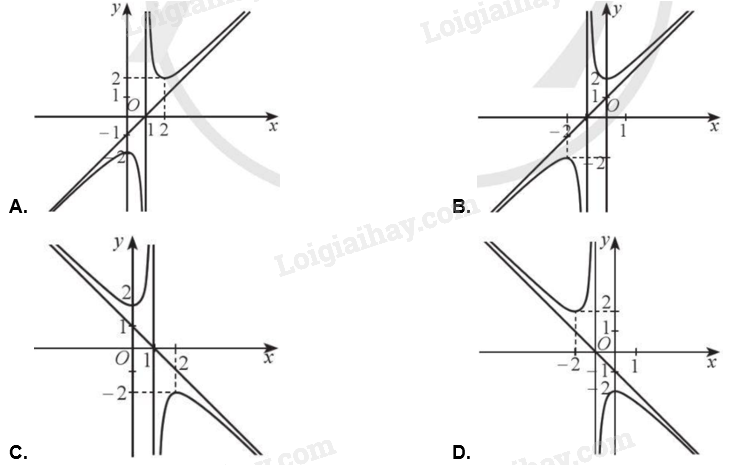
Đồ thị hàm số \(y = \frac{{{x^2} + 2{\rm{x}} + 2}}{{x + 1}}\) là đường cong nào trong các đường cong sau?
Đường cong ở Hình 17 là đồ thị của hàm số:
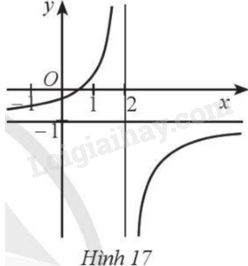
A. \(y = \frac{{1 - 2{\rm{x}}}}{{2{\rm{x}} - 4}}\).
B. \(y = \frac{{1 - {\rm{x}}}}{{{\rm{x}} - 2}}\).
C. \(y = \frac{{1 - {\rm{x}}}}{{2 - x}}\).
D. \(y = \frac{{1 - 2{\rm{x}}}}{{x - 1}}\).
Đường cong ở Hình 18 là đồ thị của hàm số:
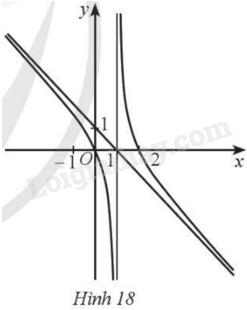
A. \(y = \frac{{{x^2} - 2{\rm{x}}}}{{x - 1}}\).
B. \(y = \frac{{{x^2} + 2{\rm{x}}}}{{ - x + 1}}\).
C. \(y = \frac{{ - {x^2} + 2{\rm{x}}}}{{2{\rm{x}} - 2}}\).
D. \(y = \frac{{ - {x^2} + 2{\rm{x}}}}{{x - 1}}\).
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a > 0\) có đồ thị là đường cong ở Hình 19. Mệnh đề nào dưới đây đúng?
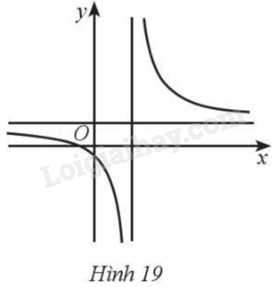
A. \(b > 0,c < 0,d < 0\).
B. \(b > 0,c > 0,d < 0\).
C. \(b < 0,c > 0,d < 0\).
D. \(b < 0,c < 0,d < 0\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{x + n}}\) có đồ thị là đường cong ở Hình 21.
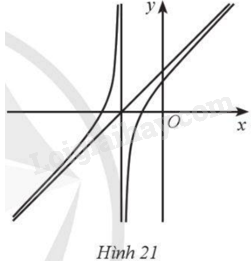
a) \(n < 0\).
b) \(a > 0\).
c) \(c > 0\).
d) \(b < 0\).
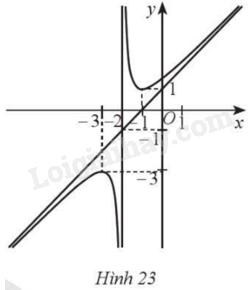
Cho hàm số \(y = f\left( x \right) = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a,m \ne 0\)) có đồ thị là đường cong như Hình 23. Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số.
c) Phương trình \(f\left( x \right) = 3\) có bao nhiêu nghiệm?
d) Tìm công thức xác định hàm số \(y = f\left( x \right)\), biết \(m = 1\).







Danh sách bình luận