Cho hai mặt phẳng \(\left( P \right):x + 2y - z + 3 = 0\) và \(\left( Q \right):x - 4y + \left( {m - 1} \right)z + 1 = 0\) với \(m\) là tham số. Tìm giá trị của tham số \(m\) để mặt phẳng \(\left( P \right)\) vuông góc với mặt phẳng \(\left( Q \right)\).
Cho hai mặt phẳng \(\left( {{\alpha _1}} \right):{A_1}x + {B_1}y + {C_1}{\rm{z}} + {D_1} = 0\) và \(\left( {{\alpha _2}} \right):{A_2}x + {B_2}y + {C_2}{\rm{z}} + {D_2} = 0\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right),\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\).
Khi đó \(\left( {{\alpha _1}} \right) \bot \left( {{\alpha _2}} \right) \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \Leftrightarrow {A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2} = 0\)
Mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {1;2; - 1} \right)\), mặt phẳng \(\left( Q \right)\) có vectơ pháp tuyến \(\overrightarrow {{n_2}} = \left( {1; - 4;m - 1} \right)\).
\(\left( P \right) \bot \left( Q \right) \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \Leftrightarrow 1.1 + 2.\left( { - 4} \right) + \left( { - 1} \right).\left( {m - 1} \right) = 0 \Leftrightarrow m = - 6\).
Các bài tập cùng chuyên đề
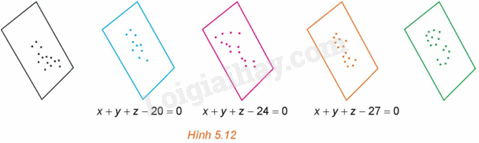
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.
a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):5x + 2y - 4z + 6 = 0\) và \(\left( \beta \right):10x + 4y - 2z + 12 = 0\)
a) Hỏi \(\left( \alpha \right)\) và \(\left( \beta \right)\) có song song với nhau hay không?
b) Chứng minh rằng điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\) nhưng thuộc mặt phẳng \(\left( \beta \right)\).
c) Viết phương trình mặt phẳng (P) đi qua \(M\left( {1; - 3;5} \right)\) và song song với \(\left( \alpha \right)\).
Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?
Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy, trần nhà tầng 1 thuộc mặt phẳng \(z - 1 = 0\), mái nhà tầng 2 thuộc mặt phẳng \(x + y + 50z - 100 = 0\). Hỏi trong ba mặt phẳng tương ứng chứa sàn nhà, trần tầng 1, mái tầng 2, hai mặt phẳng nào song song với nhau?
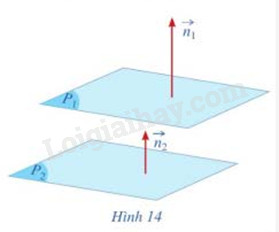
Cho mặt phẳng \(({P_1})\) có phương trình tổng quát là \(x + 2y + z + 1 = 0\) và mặt phẳng \(({P_2})\) có phương trình tổng quát là \(3x - 2y + z + 5 = 0\)
Gọi \(\overrightarrow {{n_1}} = (1;2;1),\overrightarrow {{n_2}} = (3; - 2;1)\) lần lượt là vecto pháp tuyến của hai mặt phẳng \(({P_1}),({P_2})\) (Hình 14). Hai vecto \(\overrightarrow {{n_1}} \),\(\overrightarrow {{n_2}} \) có vuông góc với nhau hay không?
Cho mặt phẳng \(({P_1}):2x + 2y + 2z + 1 = 0\) (1) và mặt phẳng \(({P_2}):x + y + z - 1 = 0\) (2).
a) Gọi \(\overrightarrow {{n_1}} = (2;2;2),\overrightarrow {{n_2}} = (1;1;1)\) lần lượt là vecto pháp tuyến của hai mặt phẳng \(({P_1}),({P_2})\) (Hình 14). Tìm liên hệ giữa \(\overrightarrow {{n_1}} \) và \(2\overrightarrow {{n_2}} \)
b) Tìm các hệ số tự do \({D_1},{D_2}\) lần lượt trong hai phương trình (1), (2). So sánh \({D_1}\) và \(2{D_2}\)
c) Nêu vị trí tương đối của hai mặt phẳng \(({P_1}),({P_2})\)
Mặt phẳng \(\left( E \right):2x - y + 8z + 1 = 0\) song song với mặt phẳng nào sau đây?
a) \(\left( F \right):8x - 4y + 32z + 7 = 0\)
b) \(\left( H \right):6x - 3y + 24z + 3 = 0\)
c) \(\left( G \right):10x - 5y + 41z + 1 = 0\)
Tìm các cặp mặt phẳng vuông góc trong các mặt phẳng sau:
\(\left( F \right):3x + 2y + 5z + 3 = 0\)
\(\left( H \right):x - 4y + z + 23 = 0\)
\(\left( G \right):x - y + 3z + 24 = 0\)
Một công trường xây dựng nhà cao tầng đã thiết lập hệ toạ độ \(Oxyz\). Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) của một toà nhà, biết:
\(\left( P \right):3x + y - z + 2 = 0\)
\(\left( Q \right):6x + 2y - 2z + 11 = 0\)
\(\left( R \right):x - 3y + 1 = 0\)
Cho ba mặt phẳng \(\left( \alpha \right):x + y + 2z + 1 = 0\), \(\left( \beta \right):x + y - z + 2 = 0\) và \(\left( \gamma \right):x - y + 5 = 0\). Trong các mệnh đề sau, mệnh đề nào sai?
A. \(\left( \alpha \right) \bot \left( \beta \right)\)
B. \(\left( \gamma \right) \bot \left( \beta \right)\)
C. \(\left( \alpha \right)\parallel \left( \beta \right)\)
D. \(\left( \alpha \right) \bot \left( \gamma \right)\)
Tìm các cặp mặt phẳng song song hoặc vuông góc trong các mặt phẳng sau:
\(\left( P \right):x + y - z + 3 = 0,\left( Q \right):2x + 2y - 2z + 99 = 0,\left( R \right):3x + 3y + 6z + 7 = 0\).
Cho ba mặt phẳng \(\left( \alpha \right):3x + 3y + 6z + 13 = 0,\left( \beta \right):2x + 2y - 2z + 9 = 0\) và \(\left( \gamma \right):x - y - 21 = 0\). Trong các mệnh đề sau, mệnh đề nào sai?
A. \(\left( \alpha \right) \bot \left( \beta \right)\).
B. \(\left( \gamma \right) \bot \left( \beta \right)\).
C. \(\left( \alpha \right)\parallel \left( \beta \right)\).
D. \(\left( \alpha \right) \bot \left( \gamma \right)\).
Cho hai mặt phẳng \(\left( \alpha \right):x - y + nz--3 = 0\) và \(\left( \beta \right):2x + my + 2z + 6 = 0\).
Với giá trị nào của \(m,n\) thì \(\left( \alpha \right)\) song song với \(\left( \beta \right)\)?
Trong không gian Oxyz, cho hình chóp S.ABC có \(S(2; - 1;7)\), \(A(2; - 1;3)\), \(B(5;2;3)\), \(C(8; - 1;3)\). Chứng minh rằng mặt phẳng (SAB) vuông góc với hai mặt phẳng (ABC) và (SBC).
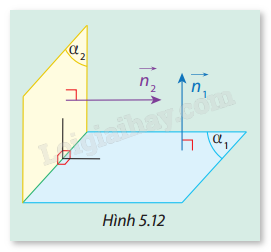
Cho hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có vectơ pháp tuyến tương ứng là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) (Hình 5.12).
a) Có nhận xét gì về góc giữa \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) khi \(({\alpha _1}) \bot ({\alpha _2})\)?
b) Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau thì \(({\alpha _1})\) và \(({\alpha _2})\) có vuông góc với nhau không? Vì sao?
Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( {{\alpha _1}} \right):2x - 3y + z + 3 = 0\), \(\left( {{\alpha _2}} \right):4x - 6y + 2z + 5 = 0\)và điểm \(M( - 2;0;1)\).
a) Hãy chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng. Có nhận xét gì về phương của các vectơ này?
b) Mặt phẳng nào đi qua điểm M?
c) Hai mặt phẳng này song song với nhau không? Vì sao?
Xét tính song song, vuông góc giữa hai mặt phẳng sau:
a) \(({\alpha _1}):x + 2y - 3z + 2 = 0\) và \(({\alpha _2}): - 2x - 4y + 6z - 5 = 0\).
b) \(({\beta _1}):x + 2z - 5 = 0\) và \(({\beta _2}):4x - 3y - 2z + 1 = 0\).
c) \(({\gamma _1}):x - 2y + z + 3 = 0\) và \(({\gamma _2}):2x - 4y + 3z + 2 = 0\).
Cho mặt phẳng \((\alpha )\): 2x + y − 3z + 8 = 0. Mặt phẳng nào sau đây vuông góc với mặt phẳng \((\alpha )\)?
A. x – 3y + 3z – 7 = 0
B. 3x – 3y + z – 7 = 0
C. x + 2y – z – 8 = 0
D. x – 2y + z + 8 = 0
Trong không gian với hệ tọa độ Oxyz cho ba mặt phẳng (P), (Q), (R) tương ứng có phương trình là 2x + 6y – 4z + 8 = 0, 5x + 15y – 10z + 20 = 0 và 6x + 18y – 12z – 24 = 0. Chọn mệnh đề đúng trong các mệnh đề sau:
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x – 3y + 4z + 20 = 0 và (Q): 4x – 13y – 6z + 40 = 40. Mệnh đề nào sau đây đúng?
