Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng 4. Mặt bên \(SAB\) là tam giác cân tại \(S\) có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy.
a) Tính góc \(\alpha \) giữa hai đường thẳng \(SD\) và \(BC\);
b) Tính góc \(\beta \) giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SCD} \right)\).
Gắn vào hệ trục toạ độ và sử dụng công thức góc giữa hai đường thẳng và góc giữa hai mặt phẳng.
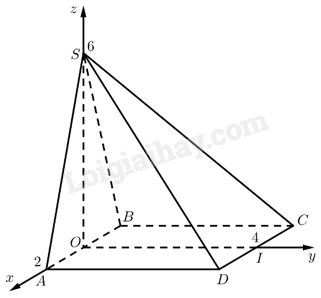
Gọi \(O\) là trung điểm của \(AB\), \(I\) là trung điểm của \(C{\rm{D}}\).
\(SAB\) là tam giác cân tại \(S\) nên \(SO \bot AB\), suy ra \(SO \bot \left( {ABCD} \right)\).
Chọn hệ trục \(Oxyz\) như hình vẽ. Ta có:
\(S\left( {0;0;6} \right),A\left( {2;0;0} \right),B\left( { - 2;0;0} \right),C\left( { - 2;4;0} \right),D\left( {2;4;0} \right)\).
a) Ta có \(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {BC} = \left( {0;4;0} \right)\), suy ra
\(\cos \left( {S{\rm{D}},BC} \right) = \left| {\cos \left( {\overrightarrow {S{\rm{D}}} ,\overrightarrow {BC} } \right)} \right| = \frac{{\left| {2.0 + 4.4 + \left( { - 6} \right).0} \right|}}{{\sqrt {{2^2} + {4^2} + {{\left( { - 6} \right)}^2}} .\sqrt {{0^2} + {4^2} + {0^2}} }} = \frac{{\sqrt {14} }}{7}\)
Vậy \(\left( {S{\rm{D}},BC} \right) \approx {57,7^ \circ }\).
b) Ta có: \(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {SA} = \left( {2;0; - 6} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {SA} } \right] = \left( { - 24;0; - 8} \right) = - 8\left( {3;0;1} \right)\).
Do đó \(\left( {SAD} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;0;1} \right)\).
\(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {CD} = \left( {4;0;0} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {CD} } \right] = \left( {0; - 24; - 16} \right) = - 8\left( {0;3;2} \right)\).
Do đó \(\left( {SCD} \right)\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {0;3;2} \right)\).
\(\cos \left( {\left( {SAD} \right),\left( {SCD} \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {3.0 + 0.3 + 1.2} \right|}}{{\sqrt {{3^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {2^2}} }} = \frac{{2\sqrt {130} }}{{130}}\)
Vậy \(\left( {\left( {SAD} \right),\left( {SCD} \right)} \right) \approx {79,9^ \circ }\).

Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho ba điểm \(A\left( {1;0; - 1} \right),B\left( {0;1;2} \right),C\left( { - 1; - 2;3} \right)\).
a) Viết phương trình mặt phẳng (ABC).
b) Viết phương trình đường thẳng AC.
c) Viết phương trình mặt cầu đường kính AC.
d) Viết phương trình mặt cầu có tâm A và đi qua B.
Trong không gian Oxyz, cho điểm \(A\left( {1;0;2} \right)\) và hai đường thẳng d: \(\frac{x}{1} = \frac{{y - 1}}{2} = \frac{z}{2}\), \(d':\frac{{x + 1}}{2} = \frac{{y + 2}}{2} = \frac{{z - 3}}{{ - 1}}\).
a) Xét vị trí tương đối của hai đường thẳng d và d’.
b) Viết phương trình đường thẳng \(\Delta \) đi qua A và song song với đường thẳng d.
c) Viết phương trình mặt phẳng (P) chứa A và d.
d) Tìm giao điểm của đường thẳng d với mặt phẳng (Oxz).
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí \(A\left( {3,5; - 2;0,4} \right)\) và sẽ hạ cánh ở vị trí \(B\left( {3,5;5,5;0} \right)\) trên đường băng EG (Hình 37).
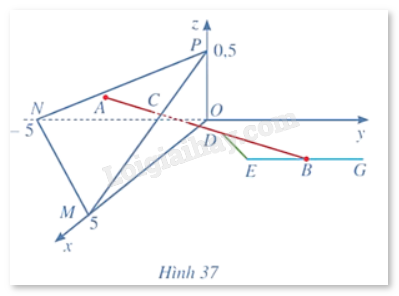
a) Viết phương trình đường thẳng AB.
b) Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy)) có nằm trong phạm vi cho phép từ \(2,{5^o}\) đến \(3,{5^o}\) hay không.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm M(5; 0; 0), N(0; -5; 0), P(0; 0; 0,5). Tìm tọa độ của điểm C là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
d) Tìm tọa độ của điểm D trên đoạn thẳng AB là vị trí mà máy bay ở độ cao 120m.
e) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5; 6,5; 0) của đường băng ở độ cao tối thiểu là 120m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).
Cho bốn điểm A(0; 1; 3), B(-1; 0; 5), C(2; 0; 2) và D(1; 1; -2).
a) Tìm tọa độ của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) và một vectơ vuông góc với cả hai vectơ đó.
b) Viết phương trình tham số và phương trình chính tắc của đường thẳng AB và AC.
c) Viết phương trình tổng quát của mặt phẳng (ABC).
d) Chứng minh rằng bốn điểm A, B, C, D không đồng phẳng.
e) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).
Trong không gian với hệ trục toạ độ Oxyz, cho hình lập phương OBCD.O'B'C'D' có O(0; 0; 0), B(a; 0; 0), D(0; a; 0), O'(0; 0; a) với a > 0.
a) Chứng minh rằng đường chéo O'C vuông góc với mặt phẳng (OB'D').
b) Chứng minh rằng giao điểm của đường chéo O'C và mặt phẳng (OB'D') là trọng tâm của tam giác OB'D'.
c) Tính khoảng cách từ điểm B' đến mặt phẳng (C'BD).
d) Tính côsin của góc giữa hai mặt phẳng (CO'D) và (C'BD).
Hình 43 minh hoạ đường bay của một chiếc trực thăng H cất cánh từ một sân bay. Xét hệ trục toạ độ Oxyz có gốc toạ độ O là chân tháp điều khiển của sân bay; trục Ox là hướng đông (Ð), trục Oy là hướng bắc (B) và trục Oz là trục thẳng đứng, đơn vị trên mỗi trục là kilômét.
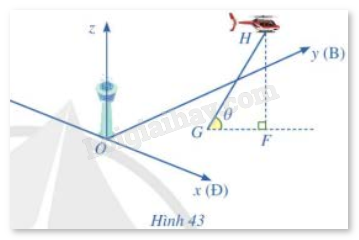
Trực thăng cất cánh từ điểm G. Vectơ \(\overrightarrow r \) chỉ vị trí của trực thăng tại thời điểm t phút sau khi cất cánh (t ≥ 0) có toạ độ là: \(\overrightarrow r = \left( {1 + t;0,5 + 2t;2t} \right)\).
a) Tìm góc θ mà đường bay tạo với phương ngang.
b) Lập phương trình đường thẳng GF, trong đó F là hình chiếu của điểm H lên mặt phẳng (Oxy).
c) Trực thăng bay vào mây ở độ cao 2 km. Tìm toạ độ điểm mà máy bay trực thăng bắt đầu đi vào đám mây.
d) Giả sử một đỉnh núi nằm ở điểm M(5; 4,5; 3). Tìm giá trị của t khi HM vuông góc với đường bay GH. Tìm khoảng cách từ máy bay trực thăng đến đỉnh núi tại thời điểm đó.
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(-688; -185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {91;75;0} \right)\) hướng về đài kiểm soát không lưu (Hình 44).
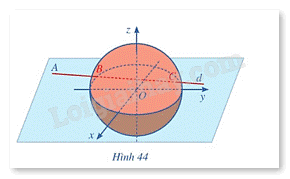
a) Xác định toạ độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
b) Xác định toạ độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.
c) Xác định toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa.
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Cho biết \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Tính góc giữa:
a) hai đường thẳng \(AC\) và \(BA'.\)
b) hai mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right).\)
c) đường thẳng \(AC'\) và mặt phẳng \(\left( {A'BD} \right).\)
Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O. Cho biết B(3;0;0), C(0;1;0), O'(0;0;2). Tính góc giữa:
a) Hai đường thẳng BO' và B'C.
b) Hai mặt phẳng (O'BC) và (OBC).
c) Đường thẳng B'C và mặt phẳng (O'BC).
Cho hình hộp chữ nhật \(OABC.O'A'B'C'\), với \(O\) là gốc toạ độ, \(A\left( {2;0;0} \right)\), \(C\left( {0;6;0} \right)\), \(O'\left( {0;0;4} \right)\). Viết phương trình:
a) Mặt phẳng \(\left( {O'AC} \right)\)
b) Đường thẳng \(CO'\)
c) Mặt cầu đi qua các đỉnh của hình hộp.
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho đường thẳng \(\Delta :\frac{{x + 2024}}{2} = \frac{{y + 2025}}{3} = \frac{{z + 2026}}{6}\) và mặt phẳng \(\left( P \right):x - 2y - 2{\rm{z}} + 1 = 0\). Gọi \(\alpha \) là góc giữa đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\).
a) Vectơ \(\overrightarrow u = \left( {2024;2025;2026} \right)\) là một vectơ chỉ phương của đường thẳng \(\Delta \).
b) Vectơ có toạ độ \(\left( {1;2;2} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).
c) \(\sin \alpha = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}}\) với \(\overrightarrow u \) là một vectơ chỉ phương của đường thẳng \(d,\overrightarrow n \) là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).
d) \(\alpha \approx {50^ \circ }\) (làm tròn đến hàng đơn vị của độ).
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho hai mặt phẳng \(\left( {{P_1}} \right):2x - 3y - 6z + 7 = 0,\left( {{P_2}} \right):2x + 2y + z + 8 = 0\). Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\).
a) Vectơ \(\overrightarrow n = \left( {2; - 3; - 6} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {{P_1}} \right)\).
b) Vectơ có toạ độ \(\left( {2; - 2;1} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {{P_2}} \right)\).
c) \(\cos \alpha = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\) với \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) lần lượt là vectơ pháp tuyến của mặt phẳng \(\left( {{P_1}} \right),\left( {{P_2}} \right)\).
d) \(\alpha \approx {69^ \circ }\) (làm tròn đến hàng đơn vị của độ).
Cho đường thẳng \(\Delta \) có phương trình tham số: \(\left\{ \begin{array}{l}x = 2 - 3t\\y = 4 + t\\z = 5 - 2t\end{array} \right.\) (\(t\) là tham số).
a) Tìm toạ độ của điểm \(M\) thuộc đường thẳng \(\Delta \), biết \(M\) có hoành độ bằng 5.
b) Chứng minh rằng điểm \(N\left( {8;2;9} \right)\) thuộc đường thẳng \(\Delta \).
c) Chứng minh rằng điểm \(P\left( { - 1;5;4} \right)\) không thuộc đường thẳng \(\Delta \). Lập phương trình tham số của đường thẳng \(\Delta '\), biết \(\Delta '\) đi qua \(P\) và song song với \(\Delta \).
d) Tìm toạ độ của điểm \(I\), biết \(I\) là giao điểm của đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right):x - y + z + 9 = 0\).
Cho mặt cầu \(\left( S \right)\) có phương trình: \({x^2} + {\left( {y + 4} \right)^2} + {\left( {z + 5} \right)^2} = 49\).
a) Xác định toạ độ tâm \({\rm{I}}\) và tính bán kính \({\rm{R}}\) của mặt cầu \(\left( S \right)\).
b) Điểm \(A\left( {0;3; - 5} \right)\) có thuộc mặt cầu \(\left( S \right)\) hay không?
c) Điểm \(B\left( {1; - 4; - 1} \right)\) nằm trong hay nằm ngoài mặt cầu \(\left( S \right)\)?
d) Điểm \(C\left( {7;3; - 5} \right)\) nằm trong hay nằm ngoài mặt cầu \(\left( S \right)\)?
e) Lập phương trình tham số của đường thẳng \(IC\).
g) Xác định toạ độ các giao điểm \(M,N\) của đường thẳng \(IC\) và mặt cầu.
Cho mặt cầu \(\left( S \right)\) có tâm \(O\left( {0;0;0} \right)\) và bán kính 2.
a) Lập phương trình mặt cầu \(\left( S \right)\).
b) Lấy các điểm \(A\left( {1;0; - 1} \right)\) và \(B\left( {1;1;0} \right)\). Lập phương trình đường thẳng \(AB\). Tìm toạ độ các điểm \(C\) và \(D\) là giao điểm của đường thẳng \(AB\) và mặt cầu \(\left( S \right)\).
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho điểm \(I\left( {1;2;3} \right)\) và đường thẳng \(\Delta :\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z + 1}}{{ - 1}}\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(I\) và vuông góc với đường thẳng \(\Delta \).
a) Nếu \(\overrightarrow u \) là một vectơ chỉ phương của đường thẳng \(\Delta \) thì \(\overrightarrow u \) là vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).
b) Vectơ có toạ độ \(\left( {2;1; - 1} \right)\) là một vectơ chỉ phương của đường thẳng \(\Delta \).
c) Vectơ có toạ độ \(\left( {2;1;1} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).
d) Phương trình mặt phẳng \(\left( P \right)\) là: \(2x + y + z - 9 = 0\).
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho hai điểm \(A\left( {0;2;0} \right)\) và \(B\left( {2; - 4;0} \right)\).
a) Trung điểm \(I\) của đoạn thẳng \(AB\) có toạ độ là \(\left( {1; - 1;0} \right)\).
b) \(AB = 40\).
c) Mặt cầu \(\left( S \right)\) tâm \(A\) và đi qua \(B\) có bán kính \(R = \sqrt {10} \).
d) Phương trình mặt cầu \(\left( S \right)\) tâm \(A\) và đi qua \(B\) là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {z^2} = 10\).
Cho bốn điểm \(A\left( {0;1;1} \right),B\left( { - 1;0;3} \right),C\left( {0;0;2} \right)\) và \(D\left( {1;1; - 2} \right)\).
a) Tìm toạ độ của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
b) Lập phương trình tham số của các đường thẳng \(AB\) và \(AC\).
c) Lập phương trình tổng quát của mặt phẳng \(\left( {ABC} \right)\).
d) Chứng minh rằng bốn điểm \(A,B,C,D\) không đồng phẳng.
e) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\).
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x - 3y - z + 2 = 0\) và điểm \(A\left( {1; - 1; - 2} \right)\).
a) Viết phương trình tham số của đường thẳng d đi qua A và vuông góc với mặt phẳng (P).
b) Tìm tọa độ giao điểm của đường thẳng d và mặt phẳng (P).
Trong không gian Oxyz, cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\\z = 4 - 3t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 1 - 2s\\y = 2 - s\\z = 5 + 3s\end{array} \right.\)
a) Chứng minh rằng \(d\parallel d'\).
b) Viết phương trình mặt phẳng \(\left( P \right)\) chứa \(d\) và \(d'\).
Trong không gian Oxyz, cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1\\y = 2 + \sqrt 3 t\\z = - 3 + t\end{array} \right.\)
a) Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (Oxy).
b) Tính góc giữa đường thẳng \(\Delta \) và trục Oy.
Trong không gian Oxyz, cho ba điểm \(A\left( {2;3; - 1} \right),B\left( { - 1;2;0} \right)\) và \(C\left( {3;1;2} \right)\).
a) Viết phương trình mặt phẳng (ABC).
b) Viết phương trình tham số và phương trình chính tắc của đường thẳng AB.
Trong không gian Oxyz, cho điểm \(I\left( {3; - 2; - 1} \right)\) và mặt phẳng \(\left( P \right):x - 2y - 2z + 3 = 0\).
a) Tính khoảng cách từ điểm I đến mặt phẳng (P).
b) Viết phương trình mặt cầu (S) có tâm I và (S) tiếp xúc với (P).
c) Viết phương trình đường thẳng d đi qua I và d vuông góc với (P).
Trong không gian Oxyz, cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2t\\z = - 1 - 2t\end{array} \right.\) và mặt phẳng \(\left( P \right):2x + y + z + 5 = 0\).
a) Tìm tọa độ giao điểm I của đường thẳng \(\Delta \) và mặt phẳng (P).
b) Viết phương trình đường thẳng \(\Delta '\) nằm trên mặt phẳng (P) đồng thời cắt \(\Delta \) và vuông góc với \(\Delta \).
c) Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P).
Trong không gian Oxyz, cho hai đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 + 2t\\y = - 2 + t\\z = 1 + 3t\end{array} \right.\) và \(\Delta ':\frac{{x + 2}}{3} = \frac{{y - 3}}{2} = \frac{{z - 1}}{{ - 2}}\).
a) Chứng minh rằng hai đường thẳng \(\Delta \) và \(\Delta '\) chéo nhau.
b) Viết phương trình mặt phẳng (P) chứa \(\Delta \) và song song với đường thẳng \(\Delta '\).
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 9\) và điểm \(A\left( {2; - 1;1} \right)\).
a) Tìm tâm I và bán kính R của mặt cầu (S).
b) Chứng minh rằng điểm A nằm trong mặt cầu (S).
c) Viết phương trình mặt phẳng (P) đi qua điểm A sao cho khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P) là lớn nhất.
Tính góc \(\alpha \) trong mỗi trường hợp sau:
a) \(\alpha \) là góc giữa hai vectơ \(\overrightarrow a = \left( {1;1; - 1} \right)\) và \(\overrightarrow b = \left( {5;2;7} \right)\);
b) \(\alpha \) là góc giữa hai đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 2 - \sqrt 3 t\\z = 5\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 1 - \sqrt 3 t'\\y = 7 + t'\\z = 9\end{array} \right.\).
c) \(\alpha \) là góc giữa hai mặt phẳng \(\left( P \right):4x + 2y - z + 9 = 0\) và \(\left( Q \right):x + y + 6z - 11 = 0\);
d) \(\alpha \) là góc giữa đường thẳng \(d:\frac{x}{2} = \frac{y}{{ - 1}} = \frac{z}{1}\) và mặt phẳng \(\left( P \right):{\rm{ }}x + y - z + 99 = 0\).
Người ta muốn thiết kế một quả địa cầu trong không gian \(Oxyz\) bằng phần mềm 3D.
Biết phương trình mặt cầu là
\(\left( S \right):{\left( {x - 24} \right)^2} + {\left( {y - 24} \right)^2} + {\left( {z - 24} \right)^2} = 100\) (đơn vị cm)
và phương trình đường thẳng trục xoay là
\({\rm{d}}:\frac{{x - 24}}{1} = \frac{{y - 24}}{1} = \frac{{z - 24}}{{3,25}}\).
a) Tìm toạ độ giao điểm của \(d\) và \(\left( S \right)\).
b) Tính số đo góc giữa \(d\) và trục \(Oz\). Làm tròn kết quả đến hàng phần mười của độ.

Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho điểm \(M\left( {2;0;0} \right)\) và mặt phẳng \(\left( P \right):2x - y - 2z + 11 = 0\).
a) Điểm \(A\left( {0;5;3} \right)\) thuộc mặt phẳng \(\left( P \right)\).
b) \(d\left( {M,\left( P \right)} \right) = \frac{5}{9}\).
c) Đường thẳng \(MA\) vuông góc với \(\left( P \right)\).
d) Đường thẳng \(d:\frac{{x - 7}}{1} = \frac{{y - 9}}{{ - 2}} = \frac{{z - 31}}{2}\) song song với \(\left( P \right)\).
Cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 2} \right)^2} = 2\).
a) Tinh khoảng cách từ tâm \(I\) của \(\left( S \right)\) đến mặt phẳng \(\left( {Oxy} \right)\).
b) Gọi \(J\) là điểm đối xứng của \(I\) qua gốc toạ độ \(O\). Viết phương trình mặt cầu \(\left( {S'} \right)\) tâm \(J\) và có cùng bán kính với \(\left( S \right)\).







Danh sách bình luận