Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC.

- Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau
- Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN=BP và suy ra \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng
Quan sát hình 9.4 để thực hiện các hoạt động.
- Các cặp góc bằng nhau của hai tam giác ABC và AMN: \(\widehat B = \widehat M{,^{}}\widehat C = \widehat N\)
- Có MN // BP, MB // NP (vì AB // NP) => MN=BP \( \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\)=> ΔABC \(\backsim\) ΔAMN

Các bài tập cùng chuyên đề
Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)
\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)
\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)
Chọn câu đúng:
-
A.
(I) đúng, (II) và (III) sai.
-
B.
(I) và (II) đúng, (III) sai.
-
C.
(I) , (II), (III) đều đúng.
-
D.
(I), (II), (III) đều sai.
Cho tam giác ABC, lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
-
A.
12cm.
-
B.
24 cm.
-
C.
48 cm.
-
D.
36cm.
Cho tam giác ABC , lấy E trên cạnh BC sao cho \(\frac{{EB}}{{EC}} = \frac{2}{3}\) Qua E kẻ đường thẳng song song với AC cắt AB tại I và đường thẳng song song với AB cắt AC tại K , biết hiệu chu vi tam giác EKC và chu vi tam giác BEI bằng 24 cm thì chu vi tam giác BEI là
-
A.
12cm .
-
B.
24 cm.
-
C.
48 cm.
-
D.
36 cm.
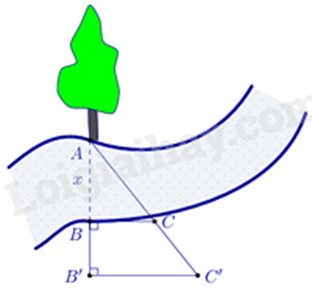
Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\)m, \(BC = 30\)m và \(B'C' = 40\)m. Tính độ rộng \(x\) của khúc sông.
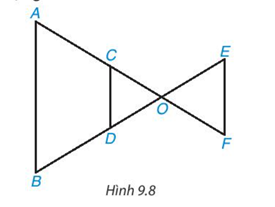
Trong hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng.
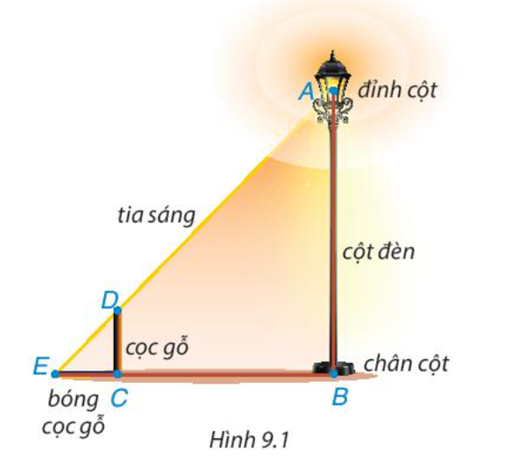
Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Hãy giải thích bác Dương đã tính được chiều cao cột đèn như thế nào, biết cọc gỗ cao 1m, EC=80cm và EB=4m.
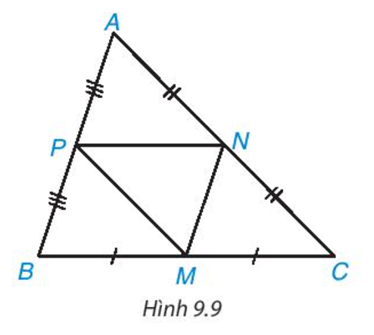
Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng
Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3m
a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?
b) Vào buổi chiều khi bóng bạn An dài 3m, hỏi bóng cột cờ dài bao nhiêu mét?
Cho hình 9.73, biết rằng MN // AB, MP // AC. Hãy liệt kê ba cặp hai tam giác (khác nhau) đồng dạng có trong hình

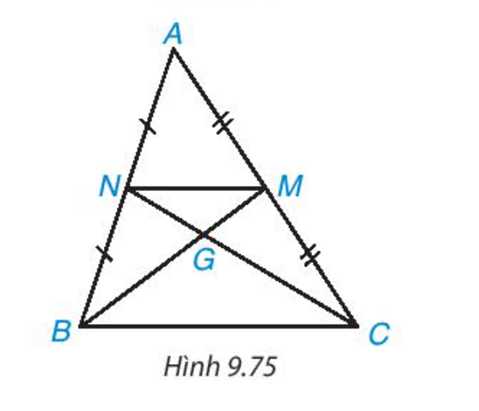
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng
Từ căn hộ chung cư nhà mình, bạn Lan đứng cách cửa sổ 1m nhìn sang tòa nhà đối diện thì vừa nhìn thấy đúng tất cả 6 tầng của tòa nhà đó. Biết rằng cửa sổ nhà Lan cao 80cm và mỗi tầng của tòa nhà đối diện 4m. Hỏi khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là bao nhiêu?
Hình sau mô tả một dụng cụ đo bề dày (nhỏ hơn 1cm) của số sản phẩm. Dụng cụ này gồm một thướng AC = 10 cm, có vạch chia đến 1 mm, gắn với một bản kim loại có cạnh thẳng AB sao cho khoảng cách BC = 1cm.

Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khhi đó trên thước ta đọc đường "bề dày" d của vật (trên hình vẽ ta có d = 5,5mm). Hãy giả thích tại sao với dụng cụ đó, ta có thể đo được bề dày d của các vật (với d < 10 mm)
Cho tam giác \(DEF\) và tam giác \(ABC\) có \(DE = \frac{1}{3}AB,DF = \frac{1}{3}AC,\widehat D = \widehat A\) (Hình 5). Trên tia \(AB\), lấy điểm \(M\) sao cho \(AM = DE\). Qua \(M\) kẻ \(MN//BC\left( {N \in AC} \right)\).
a) So sánh \(\frac{{AM}}{{AB}}\) và \(\frac{{AN}}{{AC}}\)
b) So sánh \(AN\) với \(DF\).
c) Tam giác \(AMN\) có đồng dạng với tam giác \(ABC\) không?
d) Dự đoán sự đồng dạng của hai tam giác \(DEF\) và \(ABC\).

Cho hai tam giác \(ABC\) và \(A'B'C'\) có \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\) (Hình 9).
Trên cạnh \(AC\), lấy điểm \(D\) sao cho \(DC = A'C'\). Qua \(D\) là kẻ đường thẳng song song với \(AB\) cắt cạnh \(BC\) tại \(E\).
a) Tam giác \(DEC\) có đồng dạng với tam giác \(ABC\) không?
b) Nhận xét về mối quan hệ giữa tam giác \(A'B'C'\)và tam giác \(DEC\).
c) Dự đoán về sự đồng dạng của hai tam giác \(A'B'C'\)và \(ABC\).

Nếu \(\Delta ABC\) có \(MN//AB\) (với \(M \in AC,N \in BC\)) thì
A. \(\Delta CMN\backsim\Delta ABC\).
B. \(\Delta CNM\backsim\Delta CAB\).
C. \(\Delta CNM\backsim\Delta ABC\).
D. \(\Delta MNC\backsim\Delta ABC\).
Cho tam giác ABC. Gọi B’, C’ lần lượt là trung điểm của AB, AC. Chứng minh \(\Delta AB'C' \backsim \Delta ABC\).
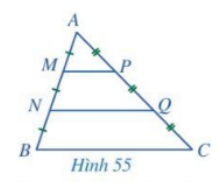
Cho tam giác ABC (Hình 55), các điểm M, N thuộc cạnh AB thỏa mãn \(AM = MN = NB\), các điểm P, Q thuộc cạnh AC thỏa mãn \(AP = PQ = QC\). Tam giác AMP đồng dạng với những tam giác nào?
Cho hình bình hành ABCD. Một đường thẳng đi qua D lần lượt cắt đoạn thẳng BC và tia AB tại M và N sao cho điểm M nằm giữa hai điểm B và C. Chứng minh:
a) \(\Delta NBM \backsim \Delta NAD\)
b) \(\Delta NBM \backsim \Delta DCM\)
c) \(\Delta NAD \backsim \Delta DCM\)
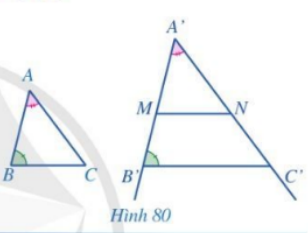
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) và \(A'B' \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A'M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A'MN = \Delta ABC\). Từ đó suy ra \(\Delta A'B'C' \backsim \Delta ABC\).
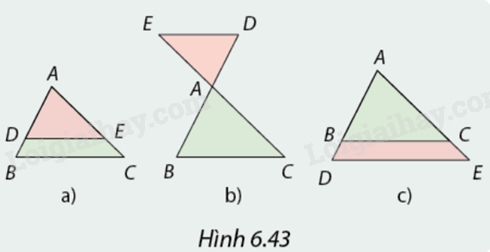
Vẽ tam giác \(ABC\) bất kì. Vẽ đường thẳng song song với \(BC,\) cắt \(AB\) tại \(D,AC\) tại \(E\) (Hình 6.43). Theo em, tam giác \(ADE\) có đồng dạng với tam giác \(ABC\) không?
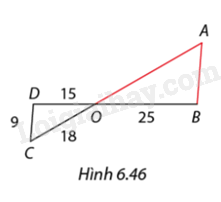
Trong Hình 6.46, \(AB\) và \(CD\) song song với nhau. Tìm độ dài \(AO\) và \(AB.\)

Cánh buồm trên thực tế và ảnh chụp của nó \(\left( {\Delta ABC} \right)\) trong hình 6.47 có thể xem là hai tam giác vuông đồng dạng. Độ dài ba cạnh của cánh buồm trên ảnh chụp là \(3,3cm;3,5cm\) và \(1,6cm.\) Trên thực tế, cạnh ngắn nhất của cánh buồm là \(4m.\) Tính độ dài hai cạnh còn lại của cánh buồm theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
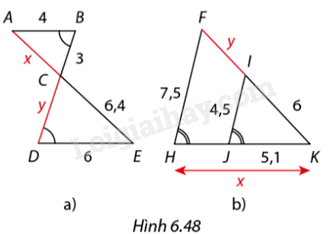
Tìm độ dài \(x,y\) trong mỗi trường hợp ở Hình 6.48.
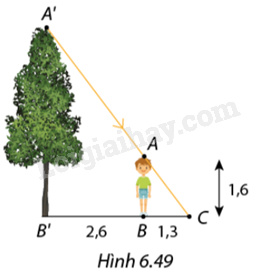
Vào một thời điểm trong ngày, bóng của ngọn cây vừa trùng đúng với bóng của đỉnh đầu bạn Nam (Hình 6.49). Biết Nam cao \(1,6m,\) độ dài bóng của Nam là \(1,3m,\) khoảng cách từ gốc cây đến vị trí Nam đứng là \(2,6m.\) Tính chiều cao của cây.
Hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo cắt nhau tại \(O.\) Đường thẳng qua \(O\) song song với \(CD,\) cắt \(AD\) tại \(E\) và cắt \(BC\) tại \(F.\) Chứng minh rằng \(O\) là trung điểm của \({\rm{EF}}.\)
Xét tam giác \(ABC\) và tam giác \(A'B'C'\) có độ dài cạnh như trong hình 6.52.
Đường thẳng \(DE\) song song với cạnh \(BC.\)
1. Vì sao \(\Delta ADE∽\Delta ABC?\)
2. Tính độ dài \(AE\) và \(DE\). Vì sao \(\Delta ADE = \Delta A'B'C'?\)
Em có kết luận gì về \(\Delta \,ABC\)và \(\Delta A'B'C'?\)

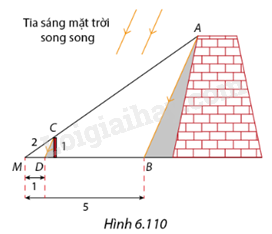
Vào một thời điểm trong ngày, \(B\) và \(D\) lần lượt là các bóng của điểm \(A\) trên mặt thành cổ và điểm \(C\) trên đỉnh cột lên mặt đất, các điểm \(M,C,A\) thẳng hàng và các điểm \(M,D,B\) thẳng hàng (Hình 6.110). Người ta đo được các khoảng cách \(MD = 1m,MB = 5m\) và \(MC = 2m.\)
a) Tính khoảng cách giữa hai điểm \(C\) và \(A.\)
b) Biết chiều cao của cây cột là \(1m,\) tính chiều cao của thành cổ.

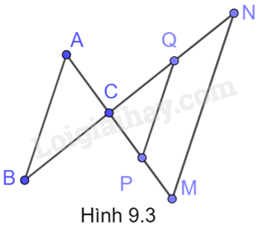
Trong Hình 9.3, cho PQ và MN cùng song song với AB. Hãy liệt kê ba cặp tam giác phân biệt đồng dạng với nhau.
Cho hình bình hành ABCD có E, F lần lượt là trung điểm của AB và AC. Chứng minh $\Delta AEF\backsim \Delta CDA$
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết \(\widehat {ABC} = \widehat {MNP}\) và \(BC = 2NP\). Chứng minh $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng.







Danh sách bình luận