Trong lí thuyết tài chính, giá trị sổ sách là giá trị của một tài sản mà công ty sử dụng để xây dựng bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt tài sản đó
Giả sử một công ty vừa mua một chiếc máy photocopy mới với giá 18 triệu đồng. Công ty lựa chọn cách tính khấu hao chiếc máy photocopy này theo phương pháp khấu hao đường thẳng trong thời gian 3 năm, tức là mỗi năm giá trị của chiếc máy photocopy sẽ giảm 18:3=6 triệu đồng
a) Viết hàm số bậc nhất biểu thị giá trị sổ sách V(x) của máy photocopy dưới dạng một hàm số theo thời gian sử dụng x (năm) của nó
b) Vẽ đồ thị của hàm số bậc nhất y=V(x)
c) Giá trị sổ sách của máy photocopy sau 2 năm sử dụng là bao nhiêu
d) Sau thời gian sử dụng là bao lâu thì máy photocopy có giá trị sổ sách là 9 triệu đồng
a) \(V(x) = 18 - 6.x\)
b) Xác định hai điểm A, b thuộc đồ thị hàm số.
b) Thay x = 2 vào V(x) tính ra giá trị sổ sách của máy Photcopy
d) Thay y = 9 vào V(x) tìm ra x là thời gian sử dụng sau bao lâu thì máy photocopy có giá trị sổ sách là 9 triệu đồng
a) \(V(x) = 18 - 6.x\)
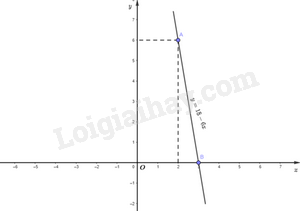
b) Vẽ đồ thị hàm số y = \(V(x) = 18 - 6.x\)
Cho x = 2 thì y = 6 ta được điểm A(2; 6) thuộc đồ thị hàm số y = 18 – 6x
Cho x = 3 thì y = 0 ta được điểm B(3; 0) thuộc đồ thị hàm số y = 18 – 6x
Đồ thị hàm số y = 18 – 6x là đường thẳng AB
c) Giá trị sổ sách của máy sau 2 năm sử dụng là: \(18 - 6.2 = 18 - 12 = 6\)(triệu đồng)
d) Ta có 9 = 18 – 6x suy ra x = 1,5
Sau 1,5 năm thì máy photocopy có giá trị sổ sách là 9 triệu đồng

Các bài tập cùng chuyên đề
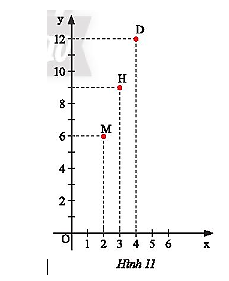
Số quyển vở \(x\) đã mua và số tiền \(y\) (nghìn đồng) phải trả của ba bạn Hùng, Dũng, Mạnh được biểu diễn lần lượt bởi ba điểm \(H,D,M\) trong mặt phẳng tọa độ \(Oxy\) như Hình 11.
Hỏi ai mua nhiều vở nhất.
Thông thường, chiều dài khuôn mặt y (cm) của một người (tính từ cằm đến đường chân tóc) gấp ba lần chiều dài tai x (cm) của người đó.
a) Viết công thức của hàm số \(y = f\left( x \right)\) biểu diễn quan hệ trên.
b) Tìm các giá trị tương ứng của hàm số trong Bảng 5.12.
c) Viết tập hợp các cặp giá trị tương ứng của \(x\) và \(y\) trong Bảng 5.12.
d) Vẽ một hệ trục tọa độ \(Oxy\). Vẽ một phần đồ thị hàm số \(y = f\left( x \right)\) với các điểm thu được từ bảng của câu b.

Cho đường thẳng \(d:y = \left( {m - 2} \right)x + 1\). Với giá trị nào của m để:
a) Đường thẳng d song song với đường thẳng \({d_1}:y = 2x + 3\).
b) Đường thẳng d cắt đường thẳng \({d_2}:y = - 5x + 1\).
Cho các đường thẳng \({d_1}:y = x + 1;{d_2}:y = - x - 3;{d_3}:y = mx + 2m - 1\).
a) Vẽ hai đường thẳng \({d_1}\) và \({d_2}\) trên cùng một mặt phẳng tọa độ Oxy.
b) Với giá trị nào của m thì đường thẳng \({d_3}\) trùng với đường thẳng \({d_2}\)?







Danh sách bình luận