Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) (làm tròn kết quả đến hàng đơn vị), biết \(\left( {{P_1}} \right):5x + 12y - 13z - 14 = 0\) và \(\left( {{P_2}} \right):13x - 5y - 12z + 7 = 0\).
‒ Hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right),\)\(\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\). Khi đó ta có:
\(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\).
Mặt phẳng \(\left( {{P_1}} \right)\) có vectơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {5;12; - 13} \right)\).
Mặt phẳng \(\left( {{P_2}} \right)\) có vectơ pháp tuyến \(\overrightarrow {{n_2}} = \left( {13; - 5; - 12} \right)\).
Côsin của góc giữa hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) bằng:
\(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {5.13 + 12.\left( { - 5} \right) - 13.\left( { - 12} \right)} \right|}}{{\sqrt {{5^2} + {{12}^2} + {{\left( { - 13} \right)}^2}} .\sqrt {{{13}^2} + {{\left( { - 5} \right)}^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{161}}{{338}}\).
Vậy \(\left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) \approx {62^ \circ }\).

Các bài tập cùng chuyên đề
Trong không gian Oxyz, hai mặt phẳng sau đây có vuông góc với nhau hay không?
\(\left( \alpha \right):3x + y - z + 1 = 0,\left( \beta \right):9x + 3y - 3z + 3 = 0\).
Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với hai vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng.
a) Góc giữa hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) và góc giữa hai giá của \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
b) Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.
Trong không gian Oxyz, tính góc giữa hai mặt phẳng \(\left( P \right):x - \sqrt 2 y + z - 2 = 0\) và \(\left( {Oxz} \right):y = 0\).
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Lấy các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) (H.5.36)

a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) có mối quan hệ gì?
b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).
Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S. ABCD, có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).

Trong không gian Oxyz, tính góc giữa mặt phẳng (P): \(x + y + z - 1 = 0\) và mặt phẳng Oxy.
Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4m; 4,4m; 4,8m. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’).
Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Gọi \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right),\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\) lần lượt là hai vectơ pháp tuyến của \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\); \({\Delta _1},{\Delta _2}\) lần lượt là giá của hai vectơ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) (Hình 33). So sánh:
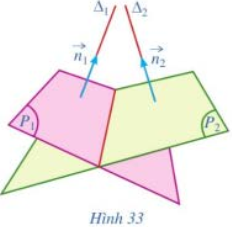
a) \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right)\) và \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\);
b) \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\) và \(\left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).
Mặt phẳng \(\left( P \right):x - 2 = 0\) vuông góc với mặt phẳng nào sau đây?
A. \(\left( {{P_1}} \right):x + 2 = 0\).
B. \(\left( {{P_2}} \right):x + y - 2 = 0\).
C. \(\left( {{P_3}} \right):z - 2 = 0\).
D. \(\left( {{P_4}} \right):x + z - 2 = 0\).
Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right):x + y + 2z - 1 = 0\) và \(\left( {{P_2}} \right):2x - y + z - 2 = 0\).
Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right):2x + 2y - z - 1 = 0\) và \(\left( {{P_2}} \right):x - 2y - 2z + 3 = 0\).
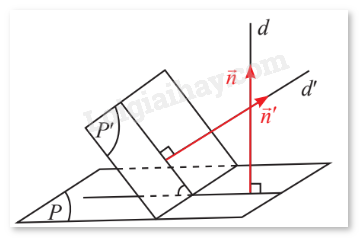
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) có vectơ pháp tuyến lần lượt là \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\), \(\vec n' = \left( {{n_1}';{n_2}';{n_3}'} \right)\) (hình dưới dây).
Gọi \(d\) và \(d'\) là hai đường thẳng lần lượt vuông góc với \(\left( P \right)\) và \(\left( {P'} \right)\). Gốc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\). So sánh \(\cos \left( {\left( P \right),\left( {P'} \right)} \right)\) và \(\cos \left( {\vec n,\vec n'} \right).\)
Tính góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right):3x + 7y - z + 4 = 0\) và \(\left( {P'} \right):x + y - 10z + 2025 = 0.\)
b) \(\left( P \right):x + y - 2z + 9 = 0\) và \(\left( {P'} \right):3x - 5y + z + 2024 = 0.\)
c) \(\left( P \right):x + z + 3 = 0\) và \(\left( {P'} \right):3y + 3z + 5 = 0.\)
Tính góc giữa hai mặt phẳng \(\left( P \right):4y + 4z + 1 = 0\) và \(\left( {P'} \right):7x + 7z + 2 = 0\).
Cho hai mặt phẳng \(\left( P \right):2x - y - z - 3 = 0\) và \(\left( Q \right):x - z - 2 = 0\). Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) bằng
A. \({30^o}\)
B. \({45^o}\)
C. \({60^o}\)
D. \({90^o}\)
Cho hai mặt phẳng \(\left( P \right):x - y - 6 = 0\) và \(\left( Q \right)\). Biết rằng điểm \(H\left( {2; - 1; - 2} \right)\) là hình chiếu vuông góc của gốc toạ độ \(O\left( {0;0;0} \right)\) xuống mặt phẳng \(\left( Q \right)\). Tính góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( Q \right)\).
Cho \(a,b\) và \(c\) khác 0, côsin của góc giữa hai mặt phẳng \(\left( P \right):ax + by + c = 0\) và \(\left( Q \right):by + cz + d = 0\) bằng:
A. \(\frac{{{b^2}}}{{\sqrt {\left( {{a^2} + {b^2} + {c^2}} \right)\left( {{b^2} + {c^2} + {d^2}} \right)} }}\).
B. \(\frac{{\left| b \right|}}{{\sqrt {\left( {{a^2} + {b^2}} \right)\left( {{b^2} + {c^2}} \right)} }}\).
C. \(\frac{{\left| b \right|}}{{\sqrt {\left( {{a^2} + {b^2} + {c^2}} \right)\left( {{b^2} + {c^2} + {d^2}} \right)} }}\).
D. \(\frac{{{b^2}}}{{\sqrt {\left( {{a^2} + {b^2}} \right)\left( {{b^2} + {c^2}} \right)} }}\).
Tính góc giữa hai mặt phẳng (làm tròn kết quả đến hàng đơn vị của độ):
\(\left( {{P_1}} \right):5x + 12y - 13z + 14 = 0\) và \(\left( {{P_2}} \right):3x + 4y + 5z - 6 = 0\).
Tính góc giữa mặt phẳng \(\left( P \right):x - y = 0\) và mặt phẳng \(\left( {Oyz} \right)\).
Trong không gian Oxyz, tính góc giữa hai mặt phẳng:
\(\left( P \right):2x - y + 2z - 1 = 0\) và \(\left( Q \right):x + y - z = 0\)
Trong không gian Oxyz, mặt sàn nằm ngang của một ngôi nhà thuộc mặt phẳng (Oxy), một mái của ngôi nhà thuộc mặt phẳng \(\left( \alpha \right):x + y + z - 1 = 0\). Hỏi mái nhà có độ dốc bằng bao nhiêu độ?
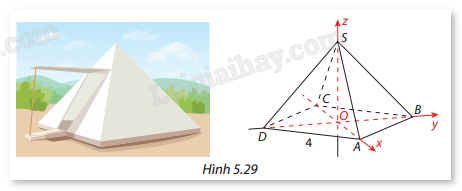
Để chuẩn bị cho chuyến đi dã ngoại, nhóm bạn Đức thiết kế lều cắm trại dạng hình chóp từ giác đều có đáy là hình vuông cạnh 4m. Theo bản vẽ thiết kế thì góc giữa hai mặt bên của lều bằng 60°. Bằng phương pháp tọa độ, hãy tính chiều cao của lều này.
Trong không gian Oxyz, tính góc giữa mặt phẳng \((\alpha ):\sqrt 3 x - y + 2 = 0\) và các mặt phẳng toạ độ \((Oxy)\), \((Oxz)\), \((Oyz)\).
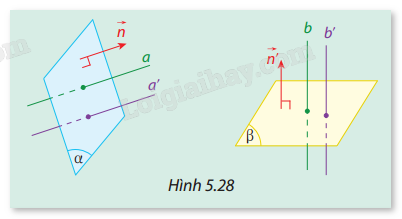
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Tính góc giữa các cặp mặt phẳng
a) \(\alpha :3x + 4y + 5z - 1 = 0\) và \(\beta :2x + y + z - 3 = 0\)
b) \(\alpha :x - y + 2z - 1 = 0\) và \(\beta :x + 2y - z + 3 = 0\)
c) \(\alpha :x + 3y - 2z - 1 = 0\) và \(\beta :4x + 2y + 5z - 3 = 0\)
Cho tứ diện OABC có \(A(a;0;0)\), \(B(0;b;0)\), \(C(0;0;c)\), (\(a > 0,b > 0,c > 0\)). Gọi \(\alpha ,\beta ,\gamma \) lần lượt là các góc giữa các mặt phẳng \((OAB)\), \((OBC)\), \((OAC)\) với mặt phẳng \((ABC)\). Chứng minh rằng:
\({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1.\)
Tính cosin của góc giữa hai mặt phẳng (P): x – 2y +3z – 8 = 0 và (Q): 3x + y – 2z + 2017 = 0.
-
A.
\(\frac{{ - 1}}{{14}}\)
-
B.
\(\frac{1}{{14}}\)
-
C.
\(\frac{5}{{14}}\)
-
D.
\(\frac{{ - 5}}{{14}}\)







Danh sách bình luận