Hình bên dưới là một đường gấp khúc có độ dài bằng 2 đơn vị. Vẽ thêm vào hình một đường gấp khúc có độ dài bằng 6 đơn vị để hình thu được là một đường gấp khúc kín có độ dài 8 đơn vị mà không có tâm đối xứng (vẽ ít nhất 2 trường hợp).
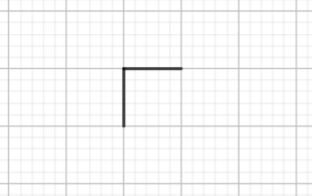
- Điểm O được gọi là tâm đối xứng của hình khi quay hình đúng nửa vòng quanh điểm O thì hình thu được chồng khít với chính nó ở vị trí ban đầu
Ta có thể vẽ thêm vào như sau:
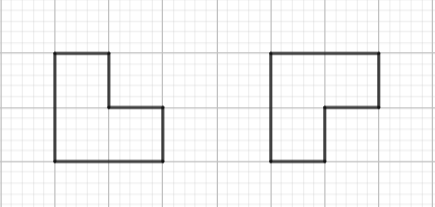
Các bài tập cùng chuyên đề
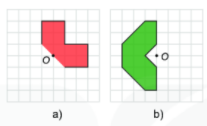
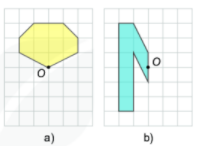
Trong mỗi hình dưới đây, điểm O có phải tâm đối xứng không?
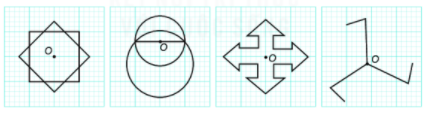
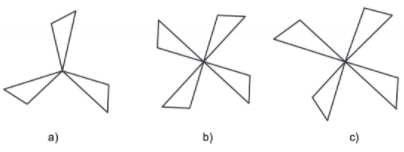
Hình nào dưới đây có tâm đối xứng? Em hãy xác định tâm đối xứng (nếu có) của chúng.
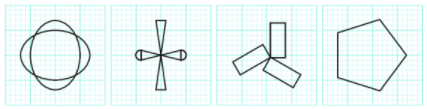
Em hãy trình bày các bước gấp và cắt giấy như trong Thực hành (cắt hình cỏ bốn lá) mục 2 đế gấp và cắt hình sau.
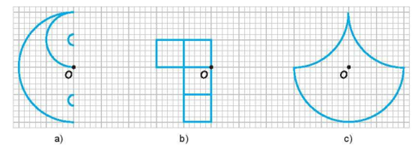
Vẽ lại các hình sau vào giấy kẻ ô vuông rồi vẽ thêm để được một hình nhận điểm O là tâm đối xứng.
An gấp những mảnh giấy kích thước 3 cm x 5 cm lần lượt theo chiều ngang và chiều dọc rồi cắt như những hình bên. Theo em, khi mở những mảnh giấy này, An sẽ nhận được chữ gì?
Hình nào dưới đây có tâm đối xứng?
Vẽ hình dưới đây vào giấy kẻ ô vuông rồi vẽ thêm để được hình nhận điểm O làm tâm đối xứng.
Tương tự như vậy, ta quan sát hình tròn (h.5.7a), hình chong chóng ba cánh (h.5.7b) và hình chong chóng bốn cánh (h.5.7c) lúc đầu và sau khi quay nửa vòng quanh điểm O như dưới đây.
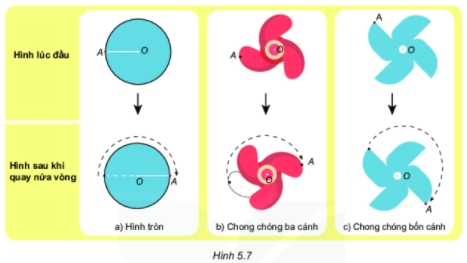
Trong ba hình trên, sau khi quay nửa vòng quanh điểm O, hình nào “chồng khít" với chính nó ở vị trí trước khi quay.
1. Đoạn thẳng là một hình có tâm đối xứng. Tâm đối xứng của nó là điểm nào?
2. Những chữ cái nào dưới đây có tâm đối xửng? Hãy dự đoán tâm đối xứng của chúng, rồi kiểm tra điều đó bằng cách quay hình nửa vòng.
3. Những hình nào dưới đây có tâm đối xứng?
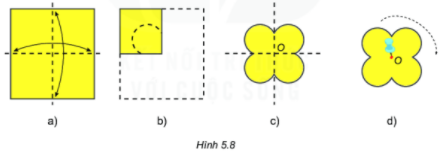
Gấp đôi tờ giấy hai lần theo hình 5.8a. Cắt tờ giấy vừa gấp theo một đường như hình 5.8b.
Mở phần cắt được ra ta có một hình bông hoa bốn cánh (1.5.8c).
Gọi giao điểm của hai nếp gấp là O. Cố định điểm O bằng đinh ghim để có thể quay hình đó quanh 0.
Bằng cách quay hình nửa vòng quanh O, em hãy kiểm tra xem điểm O có phải là tâm đối xứng của hình không.
Cắt một hình bình hành bằng giấy. Bằng cách quay hình bình hành một nửa vòng quanh giao điểm của hai đường chéo, hãy cho biết giao điểm này có là tâm đối xứng của hình bình hành không?
Bằng cách làm tương tự hoạt động 3, em hãy chỉ ra tâm đối xứng của mỗi hình dưới đây (nếu có).
Vẽ lại các hình bên vào giấy kẻ ô vuông rồi vẽ thêm để được một hình nhận điểm O là tâm đối xứng.
Ứng dụng tính đối xứng trong nghệ thuật cắt giấy
Cắt hình cỏ bốn lá theo hướng dẫn sau:
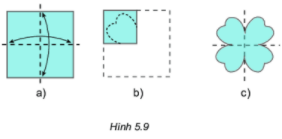
1.Chuẩn bị một mảnh giấy hình vuông kích thước 4 cm x 4 cm. Gấp đôi mảnh giấy hai lần sao cho các cạnh đối diện của nó trùng lên nhau (h.5.9a).
2.Vẽ theo hình 5.9b rồi cất theo nét vẽ, sau đó mở ra ta được hình cỏ bốn lá (h.5.9c).
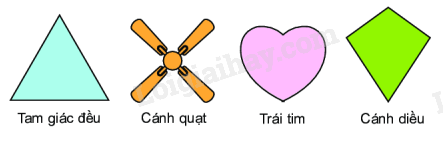
Em hãy dự đoán tâm đối xứng của các hình sau:
Cho hình vẽ sau:
Có bao nhiêu hình có tâm đối xứng?
Hãy tìm một số hình có tâm đối xứng và chỉ ra tâm đối xứng của hình đó.
Trong các hình từ Hình 66 đến Hình 69, hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra tâm đối xứng của hình đó.
Trong Hình 70, các hình từ a) đến c), hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra tâm đối xứng của hình đó ( kể cả màu sắc)
Cho các hình sau đây:
(1) Đoạn thẳng AB;
(2) Tam giác đều ABC;
(3) Hình tròn tâm O;
(4) Hình thang cân ABCD (có đáy lớn CD);
(5) Hình thoi ABCD.
Trong các hình nói trên:Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó.
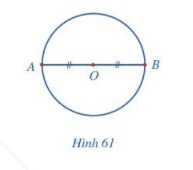
Quan sát đường kính AB của đường tròn tâm O (Hình 61).
Lấy bốn chiếc ê ke giống nhau để xếp thành hình như Hình 62.
Hình không có tâm đối xứng là:
Hãy liệt kê những hình nào trong các hình sau có tâm đối xứng: hình tam giác đều, hình bình hành, hình thang cân có hai cạnh bên không song song, hình chữ nhật, hình vuông, hình lục giác đều, hình tròn.
Trong các hình hoa văn sau, hình hoa văn nào có tâm đối xứng?
Trong các hình dưới đây, hình nào có tâm đối xứng?
Em hãy vẽ thêm vào mỗi hình dưới đây để được các hình có điểm O là tâm đối xứng.
Bạn Vuông gấp đôi tờ giấy hình chữ nhật theo chiều ngang rồi lại gấp đôi tiếp theo chiều dọc, sau đó cắt theo các nét vẽ như Hình 5.12. Theo em khi mở hình thu được ra, bạn Vuông sẽ nhận được hình gì?
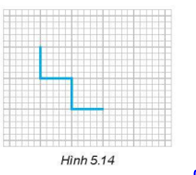
Hình 5.14 là một đường gấp khúc có độ dài bằng 4 đơn vị.
Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng 6 đơn vị để được một hình có tâm đối xứng nhưng không có trục đối xứng;
b) Một đường gấp khúc có độ dài bằng 8 đơn vị để được một hình có tâm đối xứng và có bốn trục đối xứng;
c) Một đường gấp khúc có độ dài ngắn nhất để được một hình có tâm đối xứng;
d) Một đường gấp khúc có độ dài ngắn nhất để được một hình có tâm đối xứng và có trục đối xứng.
Em hãy ghép ba tấm thẻ trong các thẻ số dưới đây để được một hình chỉ một số có ba chữ số sao cho hình đó có tâm đối xứng:
Em có thể ghép được tất cả bao nhiêu “số” như vậy?
