\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)\) bằng:
A. \(2\)
B. \(1\)
C. \( + \infty \)
D. \( - \infty \)
Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.
Từ đồ thị, ta nhận xét rằng khi \(x\) tiến tới 0 về bên phải thì \(f\left( x \right)\) tiến dần tới âm vô cực. Do vậy \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - \infty \).
Đáp án đúng là D.
Các bài tập cùng chuyên đề
Tính:\(\mathop {{\rm{lim}}}\limits_{x \to {2^ + }} \frac{{2x - 1}}{{x - 2}}\) và \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} \frac{{2x - 1}}{{x - 2}}\).
a) \(\mathop {{\rm{lim}}}\limits_{x \to 0 } \frac{2}{{\left| x \right|}}\) ;
b) \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} \frac{1}{{\sqrt {2 - x} }}\)
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\). Với cá dãy số \(\left( {{x_n}} \right)\) và \(\left( {{{x'}_n}} \right)\) cho bởi \({x_n} = 1 + \frac{1}{n},\;x{'_n} = 1 - \frac{1}{n},\) tính \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {{x_n}} \right)\) và \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {x{'_n}} \right)\).
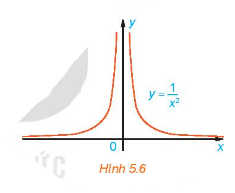
Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6. Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng \(f\left( {{x_n}} \right) \to + \infty \)
Tính các giới hạn một bên:
a) \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \frac{{x - 2}}{{x - 1}}\);
b) \(\mathop {{\rm{lim}}}\limits_{x \to {4^ - }} \frac{{{x^2} - x + 1}}{{4 - x}}\)
Cho hàm số \(f\left( x \right) = \frac{2}{{\left( {x - 1} \right)\left( {x - 2} \right)}}\)
Tìm \(\mathop {{\rm{lim}}}\limits_{x \to {2^ + }} f\left( x \right)\) và \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} f\left( x \right)\)
Tính: \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{1}{{x + 2}}.\)
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\,\,\left( {x \ne 1} \right)\) có đồ thị như ở Hình 8. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần tới đâu.
Xét tình huống ở đầu bài học. Gọi \(x\) là hoành độ điểm \(H\). Tính diện tích \(S\left( x \right)\) của hình chữ nhật \(OHMK\) theo \(x\). Diện tích này thay đổi như thế nào khi \(x \to {0^ + }\) và khi \(x \to + \infty \).
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}}\);
b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right)\).
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
a) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên trái?
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{x - 4}}\);
b) \(\mathop {\lim }\limits_{x \to {2^ +}} \frac{x}{{2 - x}}\).
\(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{1 - 3x}}{{x + 2}}\) bằng
A. \( + \infty \).
B. \( - \infty \).
C. \( - 3\).
D. \(\frac{7}{4}\).
Nếu \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty \) thì \(\mathop {\lim }\limits_{x \to a} \left[ { - f\left( x \right)} \right]\) bằng:
A. \( + \infty \)
B. \( - \infty \)
C. \(a\)
D. \( - a\)
Biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Hãy tính:
a) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{{{x^3}}}\);
b) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sin x}}{{{x^2}}}\)
c) \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{{x^2}}}\).
\(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x + 1}}{{x - 1}}\) bằng
$\mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 1}}{{x - 1}}$ bằng
Tìm $\mathop {\lim }\limits_{x \to {1^ + }} \frac{{4x - 3}}{{x - 1}}$
Trong các mệnh đề sau, mệnh đề sai là
A. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{x} = - \infty \)
B. \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \)
C. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^2}}} = - \infty \)
D. \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt[3]{x}}} = + \infty \)
