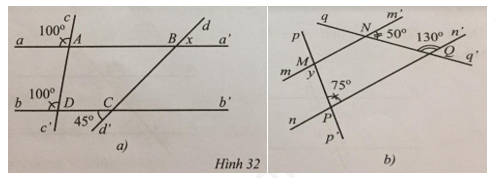
Tìm số đo x, y trong Hình 32.
Để tính số đo góc x, y, ta cần chứng minh đường thẳng a’ song song với đường thẳng b’ và đường thẳng m’ song song với đường thẳng n’.
a) Do \(\widehat {aAc} = \widehat {bDc}\) và chúng ở vị trí đồng vị nên aa’ // bb’ (Dấu hiệu nhận biết 2 đường thẳng song song)
Suy ra \(x = \widehat {bCd'} = 45^\circ \) (hai góc so le ngoài).
b) Ta có: \(\widehat {qNm'} + \widehat {m'Nq'} = 180^\circ \) (hai góc kề bù) nên \(\widehat {qNm'} = 180^\circ - \widehat {m'Nq'} = 180^\circ - 50^\circ = 130^\circ \).
Suy ra \(\widehat {qNm'} = \widehat {qQn'} = 130^\circ \). Mà 2 góc này ở vị trí đồng vị nên mm’ // nn’ (Dấu hiệu nhận biết 2 đường thẳng song song)
Vậy \(y = \widehat {pPn'} = 75^\circ \) (hai góc so le ngoài).
Các bài tập cùng chuyên đề
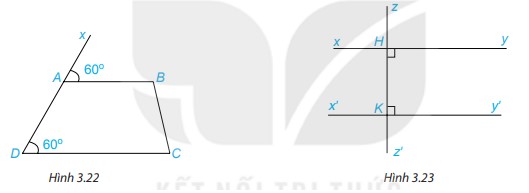
1. Quan sát Hình 3.22 và giải thích vì sao AB // CD.
2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Để vẽ đường thẳng b đi qua A và song song với a, ta có thể sử dụng góc nhọn \(60^\circ \) của êke để vẽ như sau:
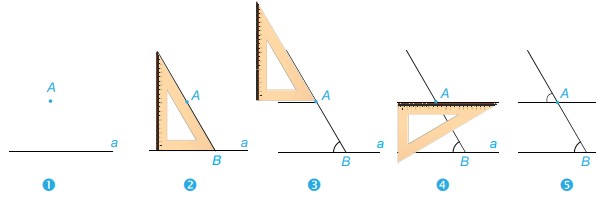
Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song song với nhau.
Dùng góc vuông hay góc 30\(^\circ \)của êke (thay cho góc 60\(^\circ \)) để vẽ đường thẳng đi qua và song song với đường thẳng a cho trước.
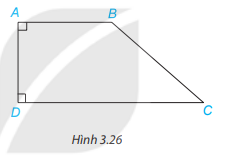
Quan sát hình 3.26, giải thích vì sao AB // DC.
Cho điểm A và đường thẳng d không đi qua A. Hãy vẽ đường thẳng d’ đi qua A và song song với d
Cho hai điểm A và B. Hãy vẽ đường thẳng a đi qua A và đường thẳng b đi qua B sao cho a song song với b.
Hãy vẽ hai đoạn thẳng AB và MN sao cho AB // MN và AB = MN
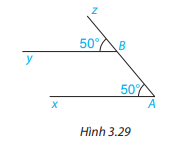
Cho Hình 3.29, biết \(\widehat {xAz} = 50^\circ \), \(\widehat {yBz} = 50^\circ \). Giải thích tại sao Ax//By.
Vẽ hình theo yêu cầu sau:
a) Vẽ hai đường thẳng d và d’ sao cho d // d’.
b) Vẽ hai đoạn thẳng AB và CD sao cho CD = 2AB và CD //AB
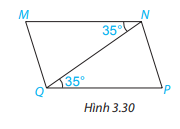
Cho Hình 3.30, biết các góc MNQ và PQN có cùng số đo bằng 35 \(^\circ \).
Chứng tỏ MN // QP.
Cho đoạn thẳng AB. Vẽ hai tia Ax, By sao cho chúng tạo với AB hai góc so le trong có cùng số đo bằng 60\(^\circ \)(\(\widehat {xAB} = \widehat {yBA} = 60^\circ \)). Trên hình vừa vẽ, hai đường thẳng chứa hai tia Ax và By có song song với nhau không? Vì sao?
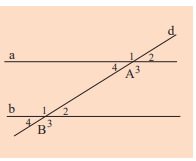
Có dấu hiệu gì về số đo của các góc đỉnh A và các góc đỉnh B trong hình bên để nhận biết hai đường thằng song song hay không?
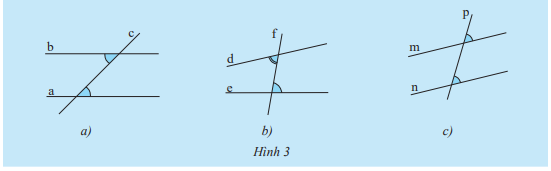
Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.
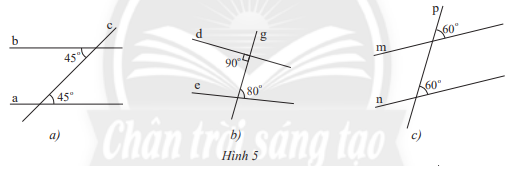
Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.
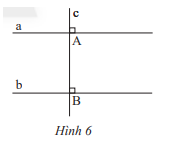
Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.
Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết
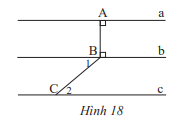
Cho Hình 18, biết \(\widehat {{B_1}} = 40^\circ ,\widehat {{C_2}} = 40^\circ \)
a) Đường thẳng a có song song với đường thẳng b không? Vì sao?
b) Đường thẳng b có song song với đường thẳng c không? Vì sao?
c) Đường thẳng a có song song với đường thẳng c không? Vì sao?
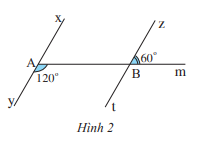
Quan sát Hình 2.
Chứng minh rằng xy // zt
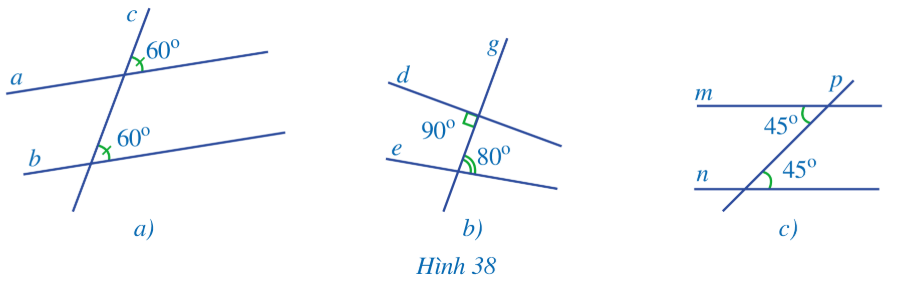
Quan sát các Hình 38a, 38b, 38c và đoán xem các đường thẳng nào song song với nhau.
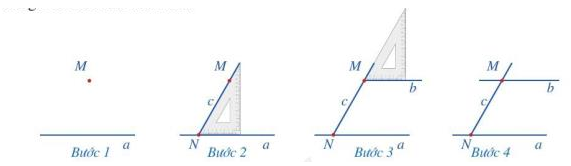
a) Thực hành vẽ đường thẳng b đi qua điểm M và song song với đường thẳng a ( M \( \notin \) a) bằng ê ke theo các bước sau:
b) Giải thích vì sao đường thẳng b song song với đường thẳng a
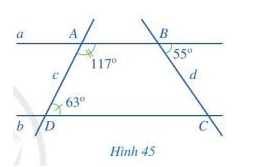
Quan sát Hình 45.
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tính số đo góc BCD.
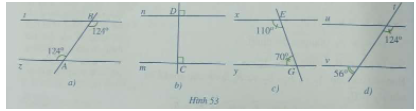
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao
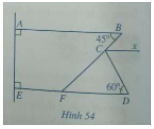
Quan sát Hình 54, trong đó Cx song song với AB.
a) Tính số đo góc BCx.
b) Chứng minh rằng Cx song song với DE.
c) Tính số đo góc BCD.
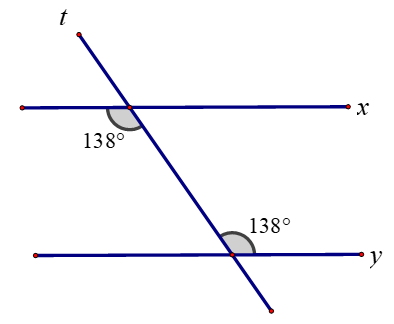
Cho hình vẽ. Khẳng định nào sau đây là đúng?
Vẽ tam giác ABC bất kì. Vẽ đường thẳng xy đi qua điểm A và song song với BC.
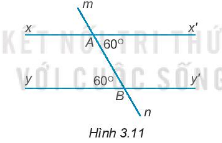
Vẽ lại hình 3.11 vào vở rồi giải thích tại sao xx’ // yy’.
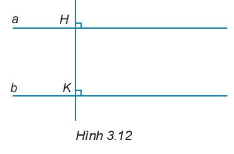
Cho hình 3.12. Giải thích tại sao \(a\parallel b\).
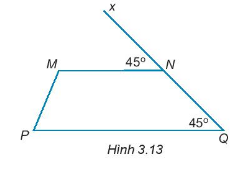
Cho hình 3.13. Giải thích tại sao \(MN\parallel PQ\).
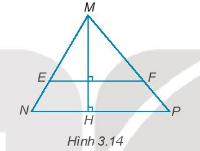
Cho hình 3.14. Giải thích tại sao \(EF\parallel NP\)
Vẽ lại hình 3.15 vào vở, biết \(NP\parallel MQ,NP = MQ\)
