Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là \(6cm\) và \(8cm\), biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
-
A.
\(480c{m^3}\)
-
B.
\(360c{m^3}\)
-
C.
\(240c{m^3}\)
-
D.
\(120c{m^3}\)
- Tính độ dài cạnh hình thoi, từ đó suy ra chu vi đáy và chiều cao lăng trụ.
- Tính diện tích đáy hình thoi \({S_{ABCD}} = \dfrac{1}{2}AC.BD\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).
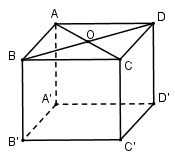
Gọi \(O = AC \cap BD\) ta có: \(OA = 3cm\,;\,OB = 4cm\)
Xét tam giác vuông $OAB$ có: \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{3^2} + {4^2}} = 5cm\).
Khi đó chu vi đáy bằng \(P = 4.5 = 20 = 2AA' \Rightarrow AA' = 10\left( {cm} \right)\)
\({S_{ABCD}} = \dfrac{1}{2}AC.BD = \dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Vậy \({V_{ABCD.A'B'C'D'}} = AA'.{S_{ABCD}} = 10.24 = 240\left( {c{m^3}} \right)\)
Đáp án : C








Danh sách bình luận