Hằng ngày, Mặt trời chiếu sáng, bóng của một tòa chung cư cao 40m in trên mặt đất, độ dài bóng của tòa nhà này được tính bằng công thức
\(S(t) = 40\left| {\cot \frac{\pi }{{12}}t} \right|\),
Ở đó S được tính bằng mét, còn t là số giờ tính từ 6 giờ sáng.
a) Tính độ dài bóng của tòa nhà tại các thời điểm 8 giờ sáng, 12 giờ trưa, 2 giờ chiều và 5 giờ 45 phút chiều.
b) Tại thời điểm nào thì độ dài bóng của tòa nhà bằng chiều cao tòa nhà?
c) Bóng tòa nhà sẽ như thế nào khi thời gian tiến dần đến 6 giờ tối?
Dựa vào công thức \(S(t) = 40\left| {\cot \frac{\pi }{{12}}t} \right|\) đề làm
a) Tại thời điểm 8 giờ sáng ta có \(t = 8 - 6 = 2\). Vậy độ dài bóng của tòa nhà tại thời điểm 8 giờ sáng là
\(\) \(S(2) = 40\left| {\cot \left( {\frac{\pi }{{12}}.2} \right)} \right| = 40\sqrt 3 \,(m)\)
Tại thời điểm 12 giờ trưa ta có \(t = 12 - 6 = 6\). Vậy độ dài bóng của tòa nhà tại thời điểm 12 giờ trưa là
\(S(6) = 40\left| {\cot \left( {\frac{\pi }{{12}}.6} \right)} \right| = 0\,(m)\)
Tại thời điểm 2 giờ chiều (14h) ta có \(t = 14 - 6 = 8\). Vậy độ dài bóng của tòa nhà tại thời điểm 2 giờ chiều là
\(S(8) = 40\left| {\cot \left( {\frac{\pi }{{12}}.8} \right)} \right| = \frac{{40\sqrt 3 }}{3}\,(m)\)
Tại thời điểm 5 giờ 45 chiều tối (17h45) ta có \(t = 17 + \frac{3}{4} - 6 = \frac{{47}}{4}\). Vậy độ dài bóng của tòa nhà tại thời điểm 2 giờ chiều là
\(S\left( {\frac{{47}}{4}} \right) = 40\left| {\cot \left( {\frac{\pi }{{12}}.\frac{{47}}{4}} \right)} \right| \approx 610,28\,(m)\)
b) Độ dài bóng của tòa nhà bằng chiều cao của tòa nhà khi
\(\begin{array}{l}S(t) = 40 \Leftrightarrow 40\left| {\cot \left( {\frac{\pi }{{12}}t} \right)} \right| = 40 \Leftrightarrow \cot \left( {\frac{\pi }{{12}}t} \right) = \pm 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \frac{\pi }{{12}}t = \pm \frac{\pi }{4} + k\pi \Leftrightarrow t = \pm 3 + 12k\,\,(k \in \mathbb{Z}).\end{array}\)
Vì \(0 \le t \le 12\) nên \(t = 3\) hoặc \(t = 9\), tức là tại thời điểm 9 giờ sáng hoặc 3 giờ chiều thì bóng của tòa nhà dài bằng chiều cao của tòa nhà.
c) Khi thời gian tiến dần đến 6 giờ tối thì t tiến dần đến 12. Vì vậy \(\frac{\pi }{{12}}t \to \pi \), do đó \(\cot \frac{\pi }{{12}}t \to - \infty \). Như vậy, bóng của tòa nhà sẽ tiến ra vô cùng.

Các bài tập cùng chuyên đề
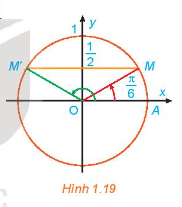
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ {0;2\pi } \right)\)
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
Giải các phương trình sau: a) \(\sin x = \frac{{\sqrt 2 }}{2}\); b) \(\sin 3x = - \sin 5x\)
Khi mặt trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là \(\alpha \left( {{0^0} \le \;\alpha \le {{360}^0}} \right)\)thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bới công thức:
\(F = \frac{1}{2}\left( {1 - \cos \alpha } \right)\).
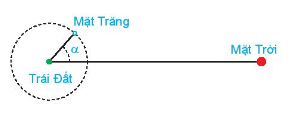
Xác định góc \(\alpha \) tương ứng với các pha sau của Mặt Trăng.
a) \(F = 0\) (trăng mới)
b) \(F = 0,25\) (trăng lưỡi liềm)
c) \(F = 0,5\) (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)
d) \(F = 1\) (trăng tròn)
Giải các phương trình sau:
a) \(2\cos x = - \sqrt 2 \); b) \(\cos 3x - \sin 5x = 0\)
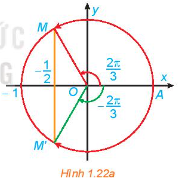
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ { - \pi ;\pi } \right)\).
b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.
Giải các phương trình sau:
a) \(\sqrt 3 \tan 2x = - 1\); b) \(\tan 3x + \tan 5x = 0\)’
a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)?\)

b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho
Giải các phương trình sau:
a) \(\cot x = 1;\) b) \(\sqrt 3 \cot x + 1 = 0\)
a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)?\)
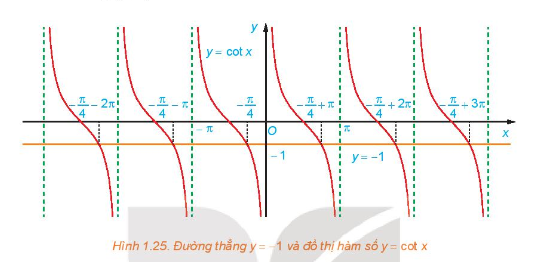
b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.
Giải các phương trình sau:
a) \(\sin x = \frac{{\sqrt 3 }}{2}\);
b) \(2\cos x = - \sqrt 2 \);
c) \(\sqrt 3 \tan \left( {\frac{x}{2} + {{15}^0}} \right) = 1\);
d) \(\cot \left( {2x - 1} \right) = \cot \frac{\pi }{5}\)
Giải các phương trình sau:
a) \(\sin 2x + \cos 4x = 0\); b) \(\cos 3x = - \cos 7x\)
Giải phương trình \(\sin 2x = \sin \left( {x + \frac{\pi }{4}} \right)\)
a) Giải phương trình: \(\sin x = \frac{{\sqrt 3 }}{2}\)
b) Tìm góc lượng giác x sao cho \(\sin x = \sin {55^ \circ }\)
a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({A_0},{B_0}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_0},{B_0}\).
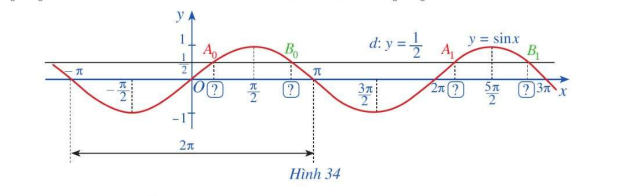
b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({A_1},{B_1}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_1},{B_1}\).
Giải phương trình được nêu trong bài toán mở đầu.
a) Giải phương trình \(\cos x = - \frac{1}{2}\)
b) Tìm góc lượng giác x sao cho \(\cos x = \cos \left( { - {{87}^ \circ }} \right)\)
a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({C_0},{D_0}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_0},{D_0}\).

b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({C_1},{D_1}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_1},{D_1}\).
a) Giải phương trình \(\tan x = 0\).
b) Tìm góc lượng giác x saoo cho \(\tan x = \tan {67^ \circ }\).
Quan sát giao điểm của đồ thị hàm số y = tan x và đường thẳng y = 1

a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó
b) Có nhận xét gì về nghiệm của phương trình tanx = 1
a) Giải phương trình \(\cot x = 1\)
b) Tìm góc lượng giác x sao cho \(\cot x = \cot \left( { - {{83}^ \circ }} \right)\)
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = -1 (Hình 37)
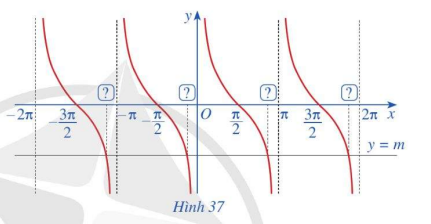
a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m trên khoảng \(\left( {0;\pi } \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.
b) Có nhận xét gì về nghiệm của phương trình cotx = -1?
Giải phương trình:
a) \(\sin \left( {2x - \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{2}\)
b) \(\sin \left( {3x + \frac{\pi }{4}} \right) = - \frac{1}{2}\)
c) \(\cos \left( {\frac{x}{2} + \frac{\pi }{4}} \right) = \frac{{\sqrt 3 }}{2}\)
d) \(2\cos 3x + 5 = 3\)
e) \(3\tan x = - \sqrt 3 \)
g) \(\cot x - 3 = \sqrt 3 \left( {1 - \cot x} \right)\)
Giải phương trình
a) \(\sin \left( {2x + \frac{\pi }{4}} \right) = \sin x\)
b) \(\sin 2x = \cos 3x\)
c) \({\cos ^2}2x = {\cos ^2}\left( {x + \frac{\pi }{6}} \right)\)
Số nghiệm của phương trình cosx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là
A.5
B.9
C.10
D.11
Số nghiệm của phương trình sinx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là:
A.10
B.6
C.5
D.11
Phương trình \(\cot x = - 1\) có nghiệm là:
A.\( - \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
B.\(\frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
C.\(\frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
D.\( - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:
A.4
B.1
C.2
D.3
Nghiệm âm lớn nhất của phương trình lượng giác \(cos2x = cos\left( {x + \frac{\pi }{3}} \right)\) là:
\(\begin{array}{l}A. - \frac{\pi }{9}\\B. - \frac{{5\pi }}{3}\\C. - \frac{{7\pi }}{9}\\D. - \frac{{13\pi }}{9}\end{array}\)
Số nghiệm của phương trình \(tanx = 3\) trong khoảng \(\left( { - \frac{\pi }{2};\frac{{7\pi }}{3}} \right)\) là
A. 1
B. 2
C. 3
D. 4
Nghiệm dương nhỏ nhất của phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\) là bao nhiêu?







Danh sách bình luận