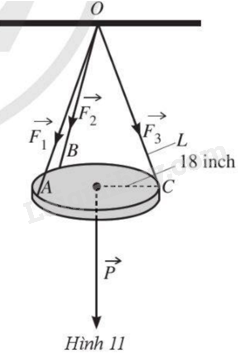
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \(O\) trên trần nhà lần lượt buộc vào ba điểm \(A,B,C\) trên đèn tròn (Hình 11). Độ dài của ba đoạn dây \(OA,OB,OC\) đều bằng \(L\left( {inch} \right)\). Trọng lượng của chiếc đèn là \(24N\) và bán kính của chiếc đèn là \(18inch\left( {1inch = 2,54cm} \right)\). Gọi \(F\) là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, \(F = F\left( L \right)\) là một hàm số với biến số là \(L\).
a) Xác định công thức tính hàm số \(F = F\left( L \right)\).
b) Khảo sát và vẽ đồ thị hàm số \(F = F\left( L \right)\).
c) Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là \(10N\).
Sơ đồ khảo sát hàm số:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
• Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm các đường tiệm cận của đồ thị (nếu có).
• Lập bảng biến thiên của hàm số, bao gồm: tính đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng.
Bước 3. Vẽ đồ thị hàm số
• Vẽ các đường tiệm cận (nếu có).
• Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục toạ độ (trong trường hợp đơn giản),…
• Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
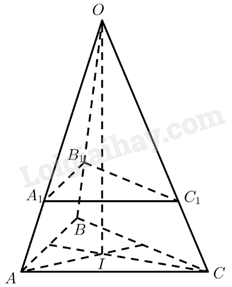
a) Gọi \({A_1},{B_1},{C_1}\)lần lượt là các điểm sao cho \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Khi đó, hai vectơ \(\overrightarrow {OA} ,\overrightarrow {O{A_1}} \) cùng phương, do đó tồn tại số \(k \ne 0\) sao cho: \(\overrightarrow {O{A_1}} = k.\overrightarrow {OA} \).
Tương tự ta có: \(\overrightarrow {O{B_1}} = k.\overrightarrow {OB} ,\overrightarrow {O{C_1}} = k.\overrightarrow {OC} \).
Suy ra, \(F = \left| {\overrightarrow {{F_1}} } \right| = k.\left| {\overrightarrow {OA} } \right| = k.L\) (1)
Do chiếc đèn ở vị trí cân bằng nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \).
Gọi \(I\) là tâm của chiếc đèn hình tròn.
Vì tam giác \(ABC\) là tam giác đều nên \(I\) cũng là trọng tâm của tam giác.
Sử dụng quy tắc trọng tâm trong tam giác \(ABC\), ta được:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OI} \Leftrightarrow \frac{1}{k}\left( {\overrightarrow {O{A_1}} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} } \right) = 3\overrightarrow {OI} \Leftrightarrow \frac{1}{k}.\overrightarrow P = 3\overrightarrow {OI} \Leftrightarrow \overrightarrow P = 3k.\overrightarrow {OI} \)
Theo giả thiết bài toán, trọng lượng của chiếc đèn là \(24N\), do đó \(OI = \frac{8}{k}\).
Mặt khác, xét hình chóp tam giác đều \(O.ABC\), có \(OI\) vuông góc mới mặt phẳng đáy \(\left( {ABC} \right)\). Khi đó: \(OI = \sqrt {O{A^2} - A{I^2}} = \sqrt {{L^2} - {{18}^2}} = \sqrt {{L^2} - 324} \).
Suy ra, \(\frac{8}{k} = \sqrt {{L^2} - 324} \Leftrightarrow k = \frac{8}{{\sqrt {{L^2} - 324} }}\) thế vào (1) ta được:
\(F = \frac{8}{{\sqrt {{L^2} - 324} }}.L \Leftrightarrow F = \frac{{8L}}{{\sqrt {{L^2} - 324} }}\left( N \right)\)
b) Ta khảo sát hàm số \(F = \frac{{8L}}{{\sqrt {{L^2} - 324} }}\) trên \(\left( {18; + \infty } \right)\).
1) Hàm số xác định trên \(\left( {18; + \infty } \right)\).
2) Sự biến thiên:
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } F = 8\).
Do đó, đường thẳng \(y = 8\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {{18}^ + }} F = + \infty \).
Do đó, đường thẳng \(x = 18\) là tiệm cận đứng của đồ thị hàm số.
• Bảng biến thiên:
\(F' = \frac{{{{\left( {8L} \right)}^\prime }.\sqrt {{L^2} - 324} - 8L.{{\left( {\sqrt {{L^2} - 324} } \right)}^\prime }}}{{{{\left( {\sqrt {{L^2} - 324} } \right)}^2}}} = \frac{{ - 2592}}{{\left( {{L^2} - 324} \right)\sqrt {{L^2} - 324} }} < 0,\forall x \in \left( {18; + \infty } \right)\).
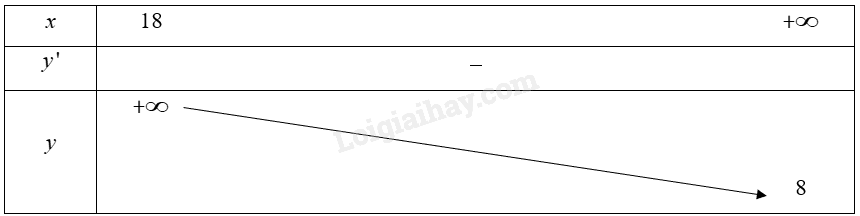
Hàm số nghịch biến trên \(\left( {18; + \infty } \right)\).
Hàm số không có cực trị trên \(\left( {18; + \infty } \right)\).
3) Đồ thị
Đồ thị hàm số không có giao điểm với trục tung.
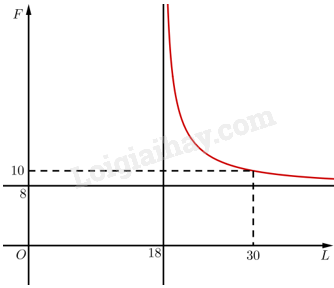
Vậy đồ thị hàm số \(F=\frac{8L}{\sqrt{{{L}^{2}}-324}}\) trên \(\left( {18; + \infty } \right)\) như sau:
c) Khi lực căng của mỗi sợi dây bằng \(10N\), ta có:
\(\frac{8L}{\sqrt{{{L}^{2}}-324}}=10\Leftrightarrow 8L=10\sqrt{{{L}^{2}}-324}\Leftrightarrow 4L=5\sqrt{{{L}^{2}}-324}\)
\(\Leftrightarrow 16{{L}^{2}}=25\left( {{L}^{2}}-324 \right)\Leftrightarrow {{L}^{2}}=900\Leftrightarrow L=30\left( TMK \right)\)
Dựa vào đồ thị hàm số \(F = \frac{{8L}}{{\sqrt {{L^2} - 324} }}\) trên \(\left( {18; + \infty } \right)\) ở phần b), ta thấy chiều dài tối thiểu của mỗi sợi dây để lực căng tối đa là \(10N\) là \(30{\rm{ }}inch\).

Các bài tập cùng chuyên đề
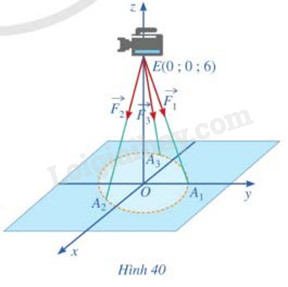
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \({A_1}(0;1;0)\), \({A_2}(\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\), \({A_3}( - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\) (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \).
Tính công sinh bởi lực \(\overrightarrow F \)= (20; 30; –10) (đơn vị: N) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển \(\overrightarrow d \)= (150; 200; 100) (đơn vị: m).

Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó.
Một phân tử metan CH4 được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện.
Góc liên kết là góc tạo bởi liên kết H–C–H là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen. Chứng minh rằng góc liên kết này gần bằng \(109,5^\circ \)
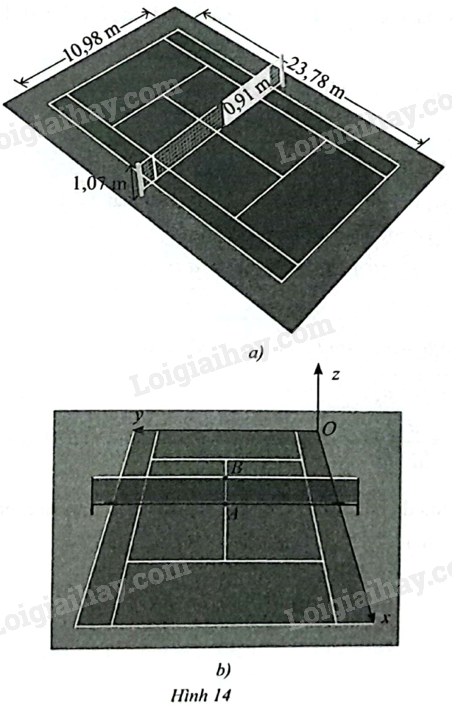
Trên một sân tennis có kích thước như trong Hình 14a), người ta đã thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên mỗi trục là m) như trong Hình 14b). Hãy xác định toạ độ của các điểm \(A,B\).
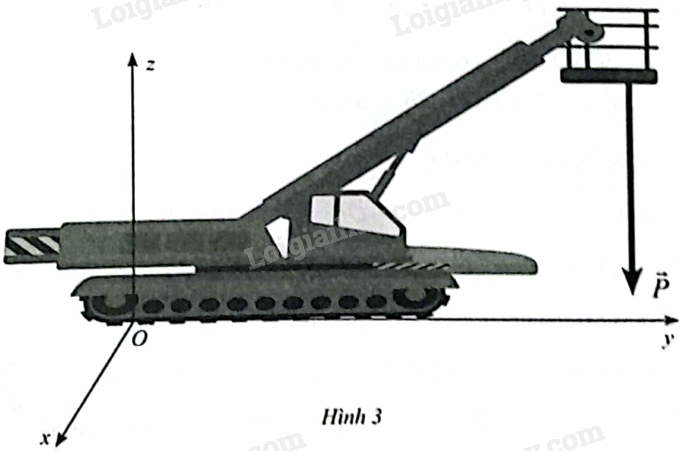
Một robot cắt cây đã di chuyển một lực \(\overrightarrow P = \left( {0;0; - 150} \right)\) (đơn vị: \(N\)) theo độ dời \(\overrightarrow d = \left( {0; - 8; - 10} \right)\) (đơn vị: \(m\)). Tính công sinh bởi lực $\overrightarrow{P}$ khi thực hiện độ dời nói trên.
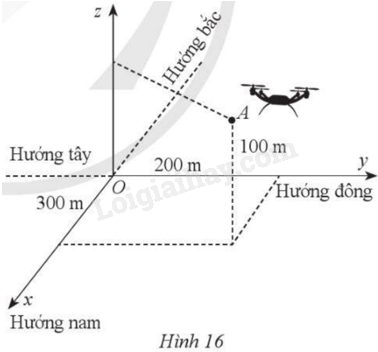
Trong quá trình cất cánh của một máy bay không người lái: Ban đầu máy bay ở vị trí \(A\), máy bay cách vị trí điều khiển 300 m về phía nam và 200 m về phía đông, đồng thời cách mặt đất 100 m (Hình 16). Một phút sau, máy bay ở vị trí \(B\) cách vị trí điều khiển 1 200 m về phía nam và 2 100 m về phía đông, đồng thời cách mặt đất 250 m.
Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) trùng với vị trí điều khiển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\) có hướng trùng với hướng nam, trục \(Oy\) có hướng trùng với hướng đông, trục \(Oz\) vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên trục tương ứng với 1 m. Hãy xác định toạ độ vectơ dịch chuyển \(\overrightarrow {AB} \) của máy bay không người lái đó.
Rađa của một trung tâm kiểm soát không lưu sân bay có phạm vi theo dõi 500 km. Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\) hướng về phía tây, trục \(Oy\) hướng về phía nam và trục \(Oz\) hướng thẳng đứng lên trời như Hình 18, trong đó đơn vị trên mỗi trục tính theo kilômét.
Hỏi rađa trung tâm kiểm soát không lưu có thể phát hiện được máy bay tại vị trí \(A\) có toạ độ \(\left( { - 200;400;200} \right)\) đối với hệ trục toạ độ trên không?

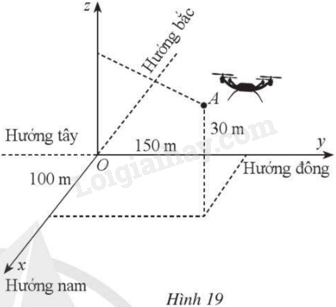
Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí \(A\) cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m (Hình 19). Để thực hiện nhiệm vụ tiếp theo, người điều khiển flycam đến vị trí \(B\) cách vị trí điều khiển 80 m về phía bắc và 120 m về phía tây, đồng thời cách mặt đất 50 m.
Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) là vị trí người điều khiển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\) có hướng trùng với hướng nam, trục \(Oy\) có hướng trùng với hướng đông, trục \(Oz\) vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên các trục tương ứng với 1 m.
a) Xác định toạ độ của flycam tại mỗi vị trí \(A,B\) đối với hệ toạ độ đã chọn.
b) Tính quãng đường flycam bay từ vị trí \(A\) đến vị trí \(B\), biết flycam bay từ vị trí \(A\) đến vị trí \(B\) theo một đường thẳng (làm tròn kết quả đến hàng đơn vị của mét).
Ở mỗi góc sân bóng đá thường được cắm một cột cờ vuông góc với mặt sân như hình bên.
a) Có thể thiết lập một hệ trục tọa độ \(Oxyz\) với gốc \(O\) là chân cột cờ, hai trục \(Ox,Oy\) lần lượt trùng với hai vạch kẻ sơn và tia \(Oz\) trùng với cột cờ hay không? Giải thích vì sao.
b) Giả sử cột cờ có chiều cao 1,5 m. Hãy xác định tọa độ của điểm đầu cột cờ đối với hệ tọa độ ở câu a (đơn vị đo trong không gian lấy theo mét).

Trong không gian xét hệ tọa độ \(Oxyz\) có gốc \(O\) trùng với vị trí của một giàn khoan trên mặt biển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt biển với trục \(Ox\) hướng về phía tây, trục \(Oy\) hướng về phía nam và trục \(Oz\) hướng thẳng đứng lên trời. Đơn vị đo được lấy theo kilômét. Tại giàn khoan người ta đặt một chiếc radar để theo dõi hành trình của một chiếc tàu ngầm hoạt động trong khu vực gần giàn khoan.
a) Hãy giải thích vì sao tọa độ của tàu ngầm luôn có dạng \(\left( {x;y;z} \right)\) với \(z \le 0\).
b) Khi nào thì tọa độ của chiếc tàu ngầm là \(\left( {x;y;0} \right)\)?

Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của một cột lần lượt là 3 m và 2 m.
Xét hệ tọa độ \(Oxyz\) sao cho mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt sân, trục \(Oz\) hướng thẳng đứng lên trời. Đơn vị trong hệ trục tọa độ được lấy theo mét.
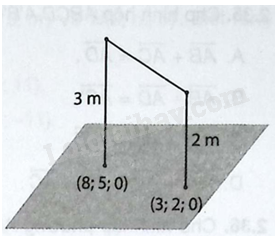
a) Biết rằng chân của hai cột có tọa độ lần lượt là \(\left( {8;5;0} \right)\) và \(\left( {3;2;0} \right)\), hãy tìm tọa độ điểm đầu của mỗi cột.
b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. Hỏi sợi dây cần có độ dài tối thiểu là khoảng bao nhiêu mét?
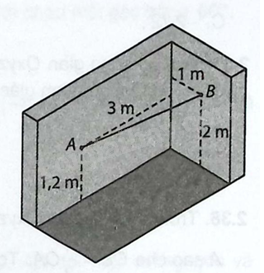
Hình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ 2 là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ 2, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m.
a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu \(A,B\) trong hệ tọa độ đó.
b) Tính độ dài của sợi dây được căng.
Một chiếc gậy có chiều dài 2,5 m được đặt trong góc phòng như hình sau đây. Một đầu của chiếc gậy nằm trên sàn nhà, cách hai bức tường lần lượt là 1 m và 0,8 m. Đầu còn lại của chiếc gậy nằm trên mép tường.
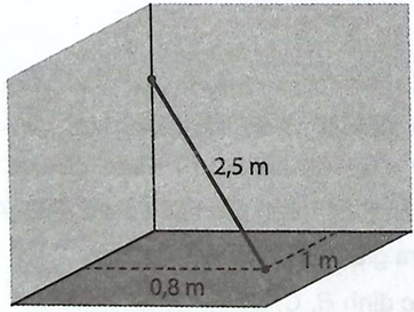
a) Hãy lập một hệ tọa độ \(Oxyz\) phù hợp và tìm tọa độ của đầu gậy nằm trên sàn nhà.
b) Tính khoảng cách từ đầu gậy trên mép tường đến sàn nhà.
Giả sử không gian ngoài vũ trụ được xét theo hệ tọa độ Oxyz, một phi thuyền ở ngoài không gian đang ở vị trí gốc tọa độ. Có 3 vệ tinh nhân tạo lần lượt ở 3 vị trí A(2500; 4700; -3600), B(3700; 1100; 2900), C(-5000; -4000; -7100), phi thuyền cần đến vị trí trọng tâm của 3 vệ tinh A, B, C để nhận và truyền tín hiệu đến các vệ tinh. Quãng đường mà phi thuyền cần di chuyển để đến được trọng tâm của 3 vệ tinh là bao nhiêu (làm tròn đến hàng đơn vị)?
Một vật ở trạng thái cân bằng khi hợp của tất cả các lực tác dụng lên vật được biểu diễn bằng vectơ-không.
Trong không gian \(Oxyz\), biết rằng đang có ba lực biểu thị bởi ba vectơ \({\vec F_1} = (9;7;2)\), \({\vec F_2} = (1;5;10)\) và \({\vec F_3} = (9; - 2; - 7)\) tác dụng lên một vật. Hãy tìm toạ độ của vectơ biểu thị lực \({\vec F_4}\) để khi tác dụng thêm lực này vào vật thì vật ở trạng thái cân bằng.
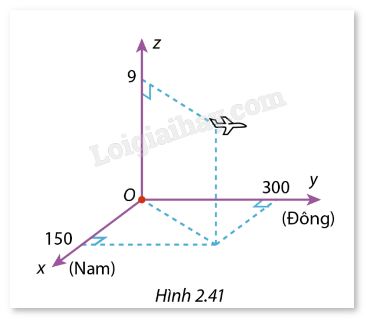
Trong Hình 2.41, gốc tọa độ O là nơi máy bay xuất phát, trục Ox theo hướng Nam, trục Oy theo hướng Đông, trục Oz theo hướng thẳng đứng. Đơn vị trên các trục là km. Vào thời điểm 9h30 sáng, máy bay ở độ cao 9 km, cách điểm xuất phát theo hướng Nam 150 km và theo hướng Đông 300 km. Phi công để chế độ bay tự động, với vận tốc theo hướng Đông 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng Bắc với vận tốc 10 m/s. Tìm tọa độ của máy bay lúc 10h30, với giả định là trong khoảng thời gian 9h30 đến 10h30, vận tốc và hướng của gió không thay đổi.
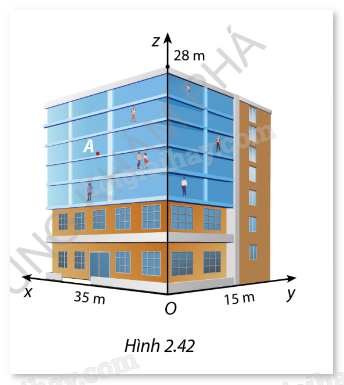
Một tòa nhà có dạng hình hộp chữ nhật với kích thước chiều dài 35 m, chiều rộng 15 m, chiều cao 28 m. Người ta định vị các vị trí trong tòa nhà dựa vào một hệ trục tọa độ Oxyz như Hình 2.42.
a) Chị Hương đang đứng ở vị trí A(20; 5; 20) và đi chuyển đến thang máy để xuống sảnh chờ đón khách. Biết vị trí vào thang máy có hoành độ x = 15 và tung độ y = 3. Hỏi chị Hương mất bao nhiêu giây để di chuyển, nếu từ vị trí A có thể đi thẳng đến cửa thang máy và chị ấy đi bộ với tốc độ 1,5 m/s?
b) Chị Hương vừa đặt một bộ phát sóng wifi trong phòng làm việc của mình tại vị trí có tọa độ (20; 5; 20). Do yêu cầu của công việc, sáng nay chị Hương phải đứng ở bàn lễ tân có tọa độ (5; 0; 0) để đón khách. Hỏi trong lúc đứng ở bàn lễ tân chờ khách thì điện thoại của chị có bắt được sóng wifi phát ra từ phòng làm việc của mình hay không? Biết rằng vùng phủ sóng bộ phát wifi nói trên có bán kính 30 mét.
Trong không gian Oxyz (đơn vị trên các trục là km), một máy bay đang bay ở độ cao 10 km, tại vị trí A(500; 200; 10). Theo hành trình dự định, máy bay sẽ phải bay qua vị trí B(700; 200; 10). Tuy nhiên do thời tiết xấu, máy bay phải chuyển hướng bay đến vị trí C(600; 300; 8).
a) Tính khoảng cách từ A đến C.
b) Hỏi trong quãng thời gian tránh vùng thời tiết xấu, máy bay đã phải bay chệch hướng dự định một góc bao nhiêu độ?
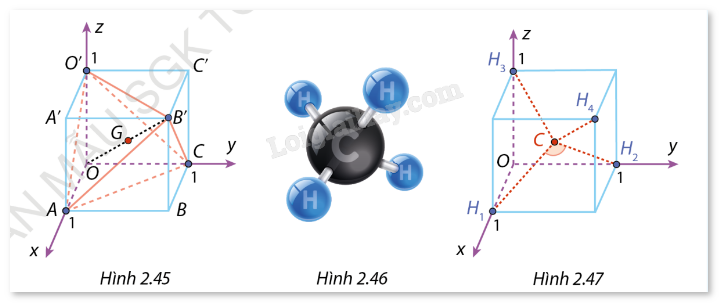
a) Trong không gian Oxyz, cho hình lập phương OABC.O’A’B’C’ với O(0;0;1), A(1;0;0), C(0;1;0) (Hình 2.45). G là trung điểm của đường chéo OB’ của hình lập phương.
- Chứng minh rằng ACO’B’ là một tứ diện đều.
- Tìm toạ độ các điểm B’ và G. Chứng minh rằng \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \vec 0\). Điểm G được gọi là trọng tâm của tứ diện đều ACO’B’.
b) Methane là một chất khí và là nguồn nguyên liệu quan trọng trong đời sống cũng như trong công nghiệp. Công thức phân tử của methane là \({\rm{C}}{{\rm{H}}_4}\). Mỗi phân tử \({\rm{C}}{{\rm{H}}_4}\) được cấu tạo bởi bốn nguyên tử hydrogen H và một nguyên tử carbon \(C\). Trong cấu tạo của phân tử methane, bốn nguyên tử hydrogen tạo thành bốn đỉnh của một tứ diện đều và nguyên tử carbon ở vị trí trọng tâm của tứ diện đó (Hình 2.46). Người ta gọi góc liên kết là góc tạo bởi liên kết \({\rm{H}} - {\rm{C}} - {\rm{H}}\). Đó là góc có hai cạnh là hai đoạn thẳng nối nguyên tử C với hai trong bốn nguyên tử H , chẳng hạn như \(\widehat {{{\rm{H}}_1}{\rm{C}}{{\rm{H}}_2}}\) (nguồn: https://www.worldatlas.com/space/why-methane-can-be-a-sign-of-life-outside-of-earth.html). Để tính góc liên kết trong phân tử methane, người ta chọn hệ trục toạ độ mà các nguyên tử hydrogen lẩn lượt nằm ở các vị trí \({H_1}(1;0;0),{H_2}(0;1;0)\), \({H_3}(0;0;1),{H_4}(1;1;1)\)(Hình 2.47). Tính số đo của góc liên kết (làm tròn kết quả đến hàng đơn vị).
Trong không gian Oxyz, một máy bay đang bay ở vị trí A(250;465;15) với tốc độ \(\vec v = (455;620;220)\) thì vào một vùng có gió với tốc độ \(\vec u = (37; - 12;4)\) (đơn vị tốc độ là km/giờ. Máy bay bay vùng gió này mất 30 phút. Tìm vị trí của máy bay sau 30 phút đó.
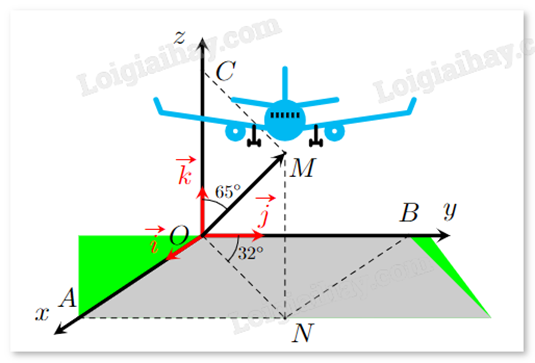
Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như hình bên dưới, cho biết M là vị trí của máy bay, OM = 14, \(\widehat {NOB} = {32^o}\), \(\widehat {MOC} = {65^o}\). Khi đó, tọa độ điểm M có dạng (a;b;c), tính a + b + c (làm tròn đến hàng phần chục).
Sử dụng phương pháp tọa độ để giải bài toán sau:
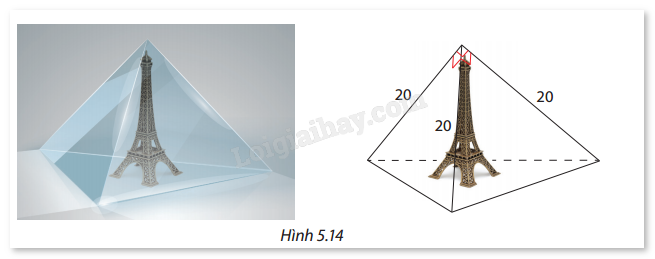
Bạn An muốn trưng bày một mô hình tháp Eiffel trong một cái hộp có dạng hình chóp tam giác đều với cạnh bên bằng 20 cm. Các mặt bên là các tam giác vuông và chân tháp nằm trên mặt đáy của cái hộp (Hình 5.14). Hỏi nếu mô hình tháp Eiffel này cao 11 cm thì có đặt được trong hộp không? Vì sao?
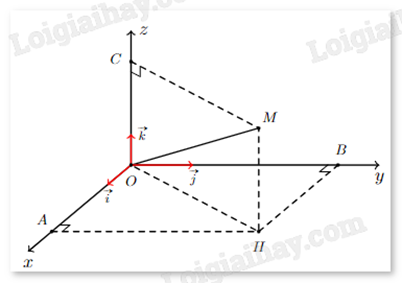
Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như hình bên. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, \(\left( {\overrightarrow i ,\overrightarrow {OH} } \right) = {64^o}\), \(\left( {\overrightarrow {OH} ,\overrightarrow {OM} } \right) = {48^o}\). Biết tọa độ của điểm M là (a;b;c), a, b, c được làm tròn đến hàng phần chục. Tính a + b – c.
Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác định vị trí của một vật thể trong không gian. Trong cùng một thời điểm, vị trí của một điểm \(M\) trong không gian sẽ được xác định bởi bốn vệ tinh cho trước nhờ các bộ thu phát tín hiệu đặt trên các vệ tinh. Giả sử trong không gian với hệ tọa độ Oxyz, có bốn vệ tinh lần lượt đặt tại các điểm \(A\left( {3;1;0} \right)\), \(B\left( {3;6;6} \right)\), \(C\left( {4;6;2} \right)\), \(D\left( {6;2;14} \right)\); vị trí \(M\left( {a;b;c} \right)\) thỏa mãn \(MA = 3,MB = 6,\)\(MC = 5,MD = 13\). Khoảng cách từ điểm \(M\) đến điểm \(O\) bằng bao nhiêu?
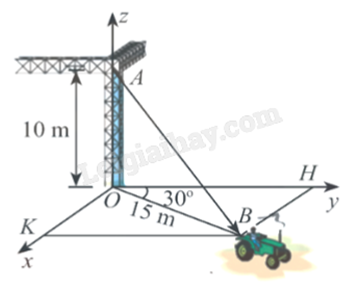
Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ Oxyz như hình vẽ với độ dài đơn vị trên các trục tọa độ bằng 1 m. Biết . Tính x + 2y – z (làm tròn kết quả đến hàng phần mười).
Hệ thống cáp treo gồm hai trụ lớn và một đường cáp nối thẳng giữa hai trụ đó (coi như độ cong không đáng kể), được đặt trong không gian với hệ tọa độ Oxyz. Một cabin cáp treo xuất phát từ điểm O(0;0;0) thuộc trụ thứ nhất và chuyển động thẳng đều theo đường cáp đến điểm A(896;2025;189) thuộc trụ thứ hai với tốc độ là 7,4 (m/s) (đơn vị trên mỗi trục là mét).
a) Điểm chính giữa của đường cáp có tọa độ là (448;1210,5;94,5).
b) Có một khu vui chơi phía dưới cáp treo nằm trong mặt phẳng (Oxy) với điểm trung tâm có tọa độ
(750,5;1497,25;0). Biết rằng từ trong cabin cáp treo có thể ngắm nhìn toàn cảnh khu vui chơi rõ nhất tại vị trí điểm \(M({x_0};{y_0};{z_0})\) cách trung tâm khu vui chơi một khoảng ngắn nhất. Khi đó ta có \({x_0} + {y_0} + {z_0} \approx 2332,5\) (kết quả làm tròn đến hàng phần mười).
c) Trên đường cáp có điểm B với hoành độ \({x_B} = 672\), khi đó thời gian để cabin đi từ điểm B đến điểm A xấp xỉ là 70 giây (kết quả làm tròn đến hàng đơn vị).
d) Độ dài đường cáp xấp xỉ bằng 2220 m (kết quả làm tròn đến hàng đơn vị).
Một kho chứa hàng có dạng hình lăng trụ đứng ABFPE.DCGQH với ABFE là hình chữ nhật và
EFP là tam giác cân tại P. Gọi T là trung điểm của DC. Các kích thước của kho chứa lần lượt là
AB = 6 m; AE = 5 m; AD = 8 m; QT = 7 m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm O thuộc đoạn AD sao cho OA = 2 m và các trục toạ độ tương ứng như hình vẽ dưới đây.
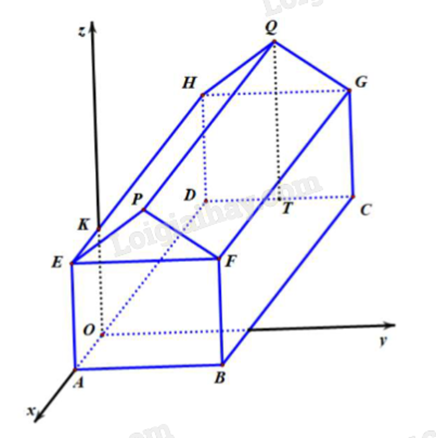
a) Tọa độ điểm Q là (-6; 3; 5).
b) Vecto \(\overrightarrow {OC} \) có tọa độ là (-6; 6; 0).
c) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm của FG và đầu thu dữ liệu đặt tại vị trí O. Người ta thiết kế đường dây cáp nối từ O đến K sau đó nối thẳng đến camera. Độ dài đoạn cáp nối tối thiểu bằng \(5 + 2\sqrt {10} \) m.
d) Mái nhà được lợp bằng tôn Hoa Sen, giá tiền mỗi mét vuông tôn là 130000 đồng. Số tiền cần bỏ ra để mua tôn lợp mái nhà là 3750000 đồng (không kể hao phí do việc cắt và ghép các miếng tôn, làm tròn kết quả đến hàng nghìn).
Trong không gian Oxyz, một khinh khí cầu ở tọa độ A(-16;-10;10) bắt đầu bay với vecto vận tốc không đổi \(\overrightarrow v = (4;3; - 1)\) (đơn vị vận tốc là km/h) và dự kiến bay trong thời gian 10 giờ. Biết trạm kiểm soát không lưu đặt ở vị trí gốc toạ độ O kiểm soát được các vật thể cách trạm một khoảng tối đa bằng 12 km. Thời gian kể từ khi trạm kiểm soát không lưu phát hiện ra khinh khí cầu đến khi khinh khí cầu ra khỏi vùng kiểm soát là bao nhiêu phút?
Một chiếc máy bay không người lái bay lên tại một điểm. Sau một thời gian bay, chiếc máy bay cách điểm xuất phát về phía Bắc 50 km và về phía Tây 20 km , đồng thời cách mặt đất 1 km. Xác định khoảng cách của chiếc máy bay với vị trí tại điểm xuất phát của nó (làm tròn kết quả đến hàng phần mười).
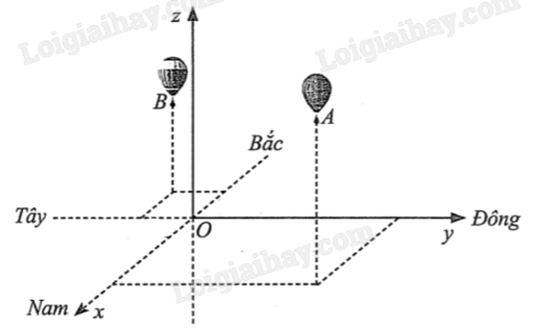
Hai chiếc khinh khí cầu A và B bay lên từ cùng một vị trí O trên mặt đất. Sau một khoảng thời gian, khinh khí cầu A nằm cách điểm xuất phát 4 km về phía Đông và 3km về phía Nam, đồng thời cách mặt đất 1 km; khinh khí cầu B nằm cách điểm xuất phát 1 km về phía Bắc và 1,5 km về phía Tây, đồng thời cách mặt đất 0,8 km (hình minh họa bên dưới). Cùng thời điểm đó, một người đứng trên mặt đất và nhìn thấy hai khinh khí cầu nói trên. Biết rằng, so với các vị trí quan sát khác trên mặt đất, vị trí người đó đứng có tổng khoảng cách đến hai khinh khí cầu là nhỏ nhất. Hỏi tổng khoảng cách nhỏ nhất ấy bằng bao nhiêu kilômét (làm tròn kết quả đến hàng phần trăm)?







Danh sách bình luận