Cho hình chóp \(S.ABC\) có đáy \(ABC\) vuông tại \(A\) và \(SB\) vuông góc với đáy. Biết \(SB = a,SC\) hợp với \(\left( {SAB} \right)\) một góc \({30^0}\) và \(\left( {SAC} \right)\) hợp với đáy \(\left( {ABC} \right)\) một góc \({60^0}\). Thể tích khối chóp là:
-
A.
\(\dfrac{{{a^3}\sqrt 3 }}{{27}}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{9}\)
-
C.
\(\dfrac{{{a^3}}}{{27}}\)
-
D.
\(\dfrac{{{a^3}}}{9}\)
- Xác định góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {SAB} \right)\), sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Xác định góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {ABC} \right)\), sử dụng định nghĩa góc giữa hai mặt phẳng là góc giữa hai đường thẳng cùng vuông góc với giao tuyến.
- Tính diện tích đáy \({S_{\Delta ABC}}\) và chiều cao \(h = SB\).
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
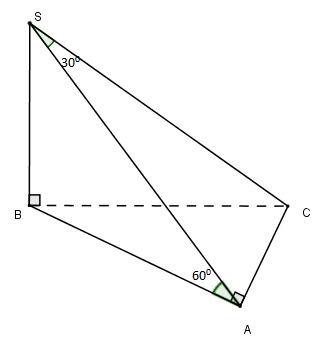
Ta có:
\(\left. \begin{array}{l}AC \bot AB\\AC \bot SB\,\,\left( {SB \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow AC \bot \left( {SAB} \right) \Rightarrow AC \bot SA\)
\( \Rightarrow SA\) là hình chiếu vuông góc của $SC$ trên $\left( {SAB} \right) \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {\left( {SC;SA} \right)} = \widehat {CSA} = {30^0}$
\(\left. \begin{array}{l}\left( {SAC} \right) \cap \left( {ABC} \right) = AC\\\left( {SAC} \right) \supset SA \bot AC\\\left( {ABC} \right) \supset AB \bot AC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SA;AB} \right)} = \widehat {SAB} = {60^0}\)
\(SB \bot \left( {ABC} \right) \Rightarrow SB \bot AB \Rightarrow \Delta SAB\) vuông tại $B$
\( \Rightarrow AB = SB.\cot {60^0} = a.\dfrac{1}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SA = \sqrt {S{B^2} + A{B^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{3}} = \dfrac{{2a}}{{\sqrt 3 }}\)
Xét tam giác vuông $SAC$ ta có: \(AC = SA.\tan {30^0} = \dfrac{{2a}}{{\sqrt 3 }}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2a}}{3}\)
\({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}\dfrac{{a\sqrt 3 }}{3}.\dfrac{{2a}}{3} = \dfrac{{{a^2}\sqrt 3 }}{9}\)
\({V_{S.ABC}} = \dfrac{1}{3}SB.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{9} = \dfrac{{{a^3}\sqrt 3 }}{{27}}\)
Đáp án : A
Các bài tập cùng chuyên đề
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó:
Cho khối chóp tam giác \(S.ABC\), trên các cạnh \(SA,SB,SC\) lần lượt lấy các điểm \(A',B',C'\). Khi đó:
Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Biết \(AC = a\sqrt 2 \), cạnh \(SC\) tạo với đáy một góc \({60^0}\) và diện tích tứ giác \(ABCD\) là \(\dfrac{{3{a^2}}}{2}\). Gọi \(H\) là hình chiếu của \(A\) trên cạnh \(SC\). Tính thể tích khối chóp \(H.ABCD\).
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\). Thể tích khối chóp là:
Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích \(V\) của tứ diện \(AMNP\) là:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
Cho hình chóp đều $S.ABCD$ có cạnh bên và cạnh đáy bằng $a$. Thể tích của khối chóp $S.ABCD$ là:
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, góc giữa cạnh bên và mặt đáy bằng \({60^0}\). Tính thể tích khối chóp $S.ABC$?
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và mặt bên hợp với đáy một góc \({60^0}\). Thể tích khối chóp $S.ABC$ là:
Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $h$, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
Cho tứ diện đều $ABCD$ có cạnh bằng $8$. Ở bốn đỉnh tứ diện, nguời ta cắt đi các tứ diện đều bằng nhau có cạnh bằng $x$, biết khối đa diện tạo thành sau khi cắt có thể tích bằng \(\dfrac{3}{4}\) thể tích tứ diện $ABCD$. Giá trị của $x$ là:
Thể tích khối bát diện đều cạnh \(a\) bằng:
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\) và \(SA = a\). Điểm $M$ thuộc cạnh $SA$ sao cho \(\dfrac{{SM}}{{SA}} = k\). Xác định $k$ sao cho mặt phẳng \(\left( {BMC} \right)\) chia khối chóp \(S.ABCD\) thành hai phần có thể tích bằng nhau.
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$
