Cho ba đường tròn (A; 10 cm), (B; 15 cm), (C; 15 cm) tiếp xúc ngoài với nhau đôi một. Đường tròn (A) tiếp xúc với (B) và (C) lần lượt tại C' và B'. Đường tròn (B) tiếp xúc với (C) tại A' (Hình 53).
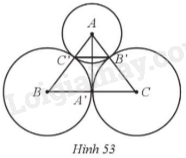
a) Chứng minh AA' là tiếp tuyến chung của đường tròn (B) và (C).
b) Tính độ dài đoạn thẳng AA′ và diện tích tam giác AB'C'.
a) Bước 1: Chứng minh A thuộc đường trung trực của BC (do \(AB = AC\)).
Bước 2: Chứng minh \(A'\) thuộc đường trung trực của BC (do\(BA' = CA'\)).
b) Bước 1: Tính \(AA'\): Áp dụng định lý Pythagore trong tam giác \(AA'B\).
Bước 2: Chứng minh \(B'C'//BC\) (áp dụng định lý Thales trong tam giác ABC), từ đó tính được B’C’.
Bước 3: Áp dụng định lý Thales trong tam giác ACA’ để tính AH.
Bước 4: Chứng minh \(AH \bot C'B'\) và tính diện tích tam giác AB’C’.
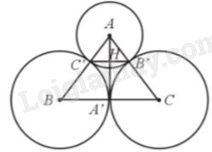
a) Ta có: \(AC' = AB' = 10\)cm (bán kính (A)),
\(BC' = BA' = 15\)cm (bán kính (B)),
\(CA' = CB' = 15\)cm (bán kính (C)).
Do \(AB = BC' + AC' = 15 + 10 = 25\)cm và \(AC = CB' + AB' = 15 + 10 = 25\)cm nên \(AB = AC\), do đó A thuộc đường trung trực của BC.
Mà \(BA' = CA' = 15\)cm nên \(A'\) thuộc đường trung trực của BC.
Suy ra \(AA'\) đường trung trực của BC, nên \(AA' \bot BC\) tại A’
Vậy \(AA'\) là tiếp tuyến chung của (B) và (C).
b) Áp dụng định lý Pythagore trong tam giác vuông \(AA'B\) có:
\(AA' = \sqrt {A{B^2} - BA{'^2}} = \sqrt {{{25}^2} - 15{'^2}} = 20\)cm.
Gọi H là giao điểm của AA’ và B’C’.
Ta có \(BC = BA' + CA' = 15 + 15 = 30\)cm.
Xét tam giác ABC có \(\frac{{AC'}}{{AB}} = \frac{{AB'}}{{AC}} = \frac{{10}}{{25}}\) nên \(B'C'//BC\) (định lý Thales đảo).
Do đó \(\frac{{B'C'}}{{BC}} = \frac{{AB'}}{{AC}}\) hay \(B'C' = \frac{{BC.AB'}}{{AC}} = \frac{{30.10}}{{25}} = 12\)cm.
Xét tam giác ACA’ có \(HB'//CA'\) nên \(\frac{{AH}}{{AA'}} = \frac{{AB'}}{{AC}}\) (định lý Thales) hay \(AH = \frac{{AB'.AA'}}{{AC}} = \frac{{10.20}}{{25}} = 8\)cm.
Ta có \(B'C'//BC,AA' \bot BC\) nên \(B'C' \bot AA'\) hay \(AH \bot C'B'\).
Diện tích tam giác \(AB'C'\) là \(\frac{1}{2}B'C'.AH = \frac{1}{2}.12.8 = 48\)cm2.
Các bài tập cùng chuyên đề
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H.
a) Xác định khoảng cách từ O đến đường thẳng a.
b) Nếu vẽ đường tròn (O; OH) thì đường tròn này và đường thẳng a có vị trí tương đối như thế nào?
Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3cm) tiếp xúc với cả bốn cạnh của hình vuông.
Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.
Trở lại tình huống mở đầu. Ở đây, ta hiểu đồng xu nằm đè lên một đường thẳng khi đường tròn (hình ảnh của đồng xu) và đường thẳng ấy cắt nhau.
Bằng cách xét vị trí của tâm đồng xu trong một dải nằm giữa hai đường thẳng song song cạnh nhau (cách đều hoặc không cách đều hai đường thẳng đó), hãy chứng minh rằng chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.
Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:
- Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;
- Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Cho tam giác vuông ABC (A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng:
a) BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA).
b) CA và CA’ là hai tiếp tuyến cắt nhau của (B; BA).
Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).
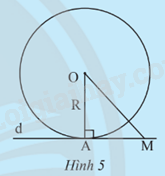
a) Giải thích tại sao ta có OA = R và OM > R.
b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.
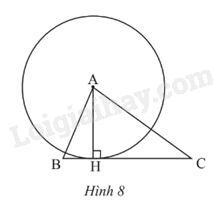
Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.
Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe, xác định các tiếp điểm.
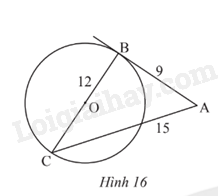
Trong Hình 16, AB = 9; BC = 12; AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:
a) \(\widehat {ACB}\) có số đo bằng 90o, từ đó suy ra độ dài của BC theo R;
b) OM là tia phân giác của \(\widehat {COA}\).
c) MC là tiếp tuyến của đường tròn (O; R).
Cho đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\). Gọi \(H\) là hình chiếu của tâm \(O\) trên đường thẳng \(a\) (Hình 33).
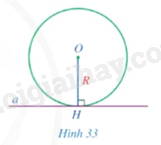
a) So sánh khoảng cách \(OH\) từ tâm \(O\) đến đường thẳng \(a\) và bán kính \(R\).
b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
c) Điểm \(H\) có phải là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) hay không?
d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm hay không?
Cho ba điểm \(A,B,C\) thẳng hàng, trong đó \(B\) nằm giữa \(A\) và \(C\). Đường tròn \(\left( O \right)\) tiếp xúc với đường thẳng \(AB\) tại điểm \(C\). Chứng minh: \(A{O^2} + B{C^2} = B{O^2} + A{C^2}\).
Cho đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) thỏa mãn đường thẳng \(a\) đi qua điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) và \(a \bot OH\).
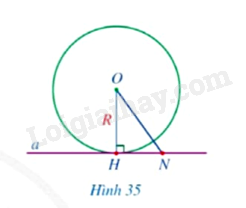
a) So sánh khoảng cách từ điểm \(O\) đến đường thẳng \(a\) và bán kính \(R\).
b) Giả sử \(N\) là điểm thuộc đường thẳng \(a\) và \(N\) khác \(H\). So sánh \(ON\) và \(R\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
c) Đường thẳng \(a\) có phải là tiếp tuyến của đường tròn \(\left( {O;R} \right)\) hay không?
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) tiếp xúc ngoài nhau tại điểm \(I\). Gọi \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\). Chứng minh \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\).
Cho hai đường tròn \(\left( O \right),\left( {O'} \right)\) cắt nhau tại hai điểm \(A,B\) sao cho đường thẳng \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\). Chứng minh đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Cho đường tròn \(\left( O \right)\) và dây \(AB\). Điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) thỏa mãn điểm \(B\) nằm trong góc \(MAO\) và \(\widehat {MAB} = \frac{1}{2}\widehat {AOB}\). Chứng minh đường thẳng \(MA\) là tiếp tuyến của đường tròn \(\left( O \right)\).
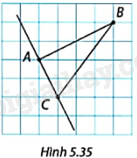
Trong Hình 5.35, cạnh mỗi hình vuông trong lưới ô vuông có độ dài là 1 đơn vị. Chứng minh rằng đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
Trên mặt phẳng tọa độ, vẽ đường tròn tâm I(2; 3) đi qua gốc tọa độ O. Vẽ tiếp tuyến của đường tròn tại O.
Cho A là một điểm thuộc đường tròn (O), M là một điểm thuộc tiếp tuyến của (O) tại điểm A (M khác A). Đường tròn tâm M bán kính MA cắt (O) tại B (B khác A). Chứng minh rằng MB là một tiếp tuyến của (O).
Trong Hình 5.40, mặt cắt của Trái Đất có thể xem là đường tròn tâm O bán kính \(R = 6\;400km\). Từ điểm A nằm ở độ cao h so với mực nước biển, một người có thể thấy xa nhất đến điểm B trên (O) sao cho AB là tiếp tuyến (O). Khoảng cách AB khi đó được gọi là tầm nhìn xa từ điểm A. Tính AB nếu \(h = 20m\).
“Nếu một đường thẳng đi qua một điểm của đường tròn và … thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là
Cho $\left( {O;5cm} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;5\,cm} \right)$, khi đó
Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
Cho tam giác \(MNP\) có \(MN = 5cm,NP = 12cm,MP = 13cm\). Vẽ đường tròn \(\left( {M;NM} \right)\). Khẳng định nào sau đây là đúng?
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
