a) Xác định parabol \((P):y = a{x^2} + bx + c\), biết rằng \((P)\) có đỉnh \(I(2; - 1)\) và cắt trục tung tại điểm có tung độ bằng -3.
b) Xét sự biến thiên và vẽ đồ thị hàm số (P) tìm được.
a) Hàm số \(y = a{x^2} + bx + c(a \ne 0)\) có đỉnh \(\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\).
b) Sự biến thiên
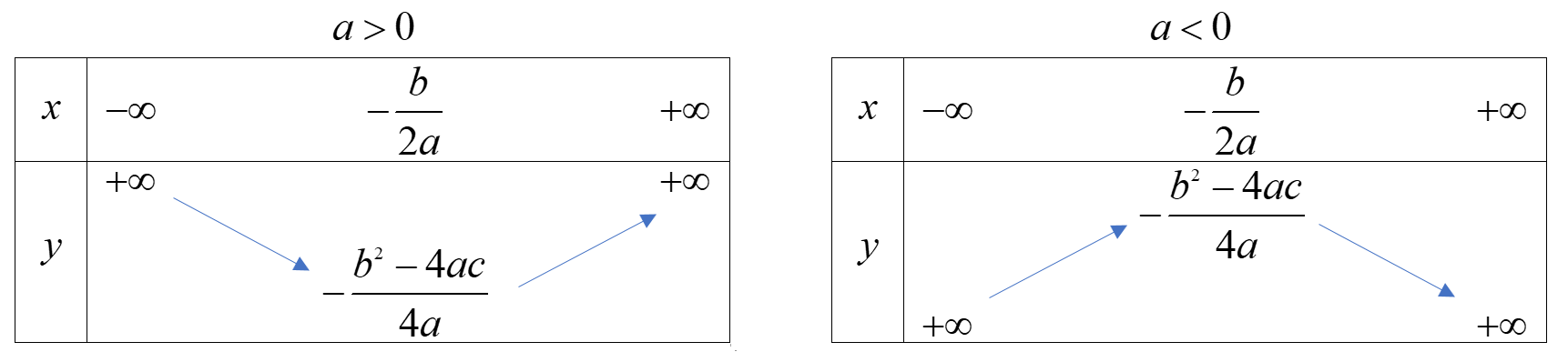
* Vẽ đồ thị
+ Đỉnh I\(\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
+ Trục đối xứng \(x = - \frac{b}{{2a}}\)
+ Giao với các trục (nếu có)
+ Lấy các điểm thuộc đồ thị (đối xứng nhau qua trục đối xứng).
a) Ta có: (P) giao với Oy tại điểm có tung độ bằng -3 hay điểm (0;-3). Suy ra \(a.0 + b.0 + c = - 3 \Leftrightarrow c = - 3\)
Vì (P) có đỉnh I(2;-1) nên \(\left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = 2\\a{.2^2} + b.2 + ( - 3) = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - b = 4a\\4a + 2b - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 2\end{array} \right.\)
Vậy parabol (P) là \(y = - \frac{1}{2}{x^2} + 2x - 3\)
b) Hàm số \(y = - \frac{1}{2}{x^2} + 2x - 3\) có \(a = - \frac{1}{2} < 0\), đỉnh I(2;-1) nên có bảng biến thiên:
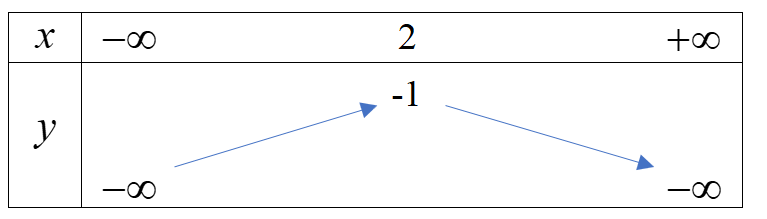
Hàm số đồng biến trên \(( - \infty ;2)\) và nghịch biến trên khoảng \((2; + \infty )\)
* Vẽ đồ thị
Đỉnh I(2;-1)
Trục đối xứng \(x = 2\)
Cắt trục tung tại A(0;-3) và không cắt Ox
Lấy B(4;-3) thuộc (P), đối xứng với A(0;-3) qua trục đối xứng
Lấy \(C\left( {1; - \frac{3}{2}} \right),D\left( {3; - \frac{3}{2}} \right)\) thuộc (P).









Danh sách bình luận