Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
-
A.
0
-
B.
1
-
C.
2
-
D.
Vô số
Theo lí thuyết, cho hai đường thẳng chéo nhau, khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Vậy nếu hai đường thẳng a và b chéo nhau thì có duy nhất một mặt phẳng chứa a và song song với b.
Đáp án : B
Các bài tập cùng chuyên đề
Trong Ví dụ 1, đường thẳng AC cắt các mặt phảng nào, nằm trong các mặt phẳng nào?
Quan sát hình ảnh khung thành bóng đá và nhận xét vị trí của xà ngang, cột dọc, thanh chống và thanh bên của khung thành với mặt đất.
Quan sát các xà ngang trên sân tập thể dục ở Hình 47. Hãy cho biết vị trí tương đối của các xà ngang đó với mặt sân.
a) Trong Hình 44, thanh barrier và mặt đường gợi nên hình ảnh đường thẳng d và mặt phẳng (P).Cho biết đường thẳng d và mặt phẳng (P) có điểm chung hay không.
b) Cho đường thẳng d và mặt phẳng (P). Hãy cho biết các khả năng có thể xảy ra đối với số điểm chung của d và (P).
Trong phòng học của lớp, hãy nêu những hình ảnh về đường thẳng song song với mặt phẳng.
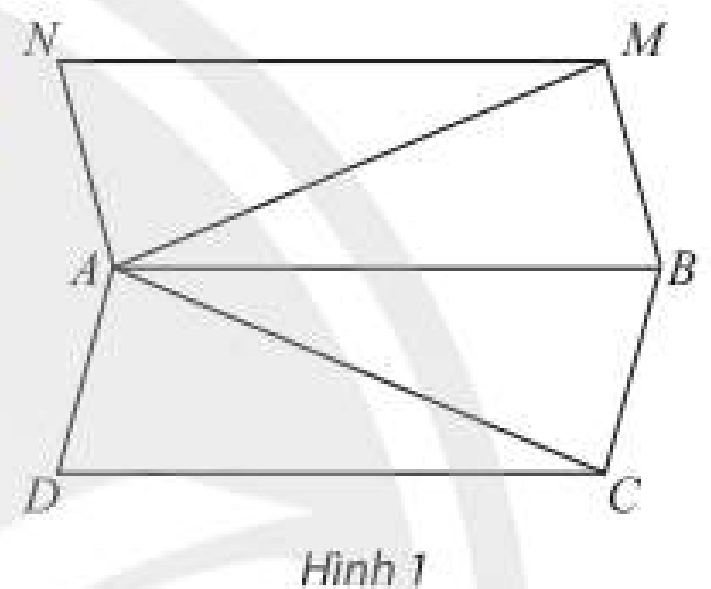
Cho \(E\) và \(F\) lần lượt là trung điểm các cạnh \(AB\) và \(AC\) của tứ diện \(ABC{\rm{D}}\). Xác định vị trí tương đối của các đường thẳng \(BC,AD\) và \(EF\) với mặt phẳng \(\left( {BCD} \right)\).
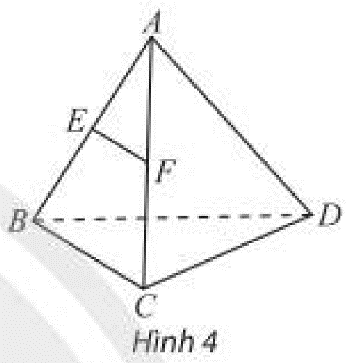
Cho hai hình bình hành \(ABCD\) và \(ABMN\) không đồng phẳng. Tìm số giao điểm của mặt phẳng \(\left( {ABCD} \right)\) lần lượt với các đường thẳng \(MN,MA\) và \(AC\).
Mô tả vị trí tương đối của các đường thẳng \(a,b,c,d,e\) với mặt phẳng \(\left( P \right)\) là mặt trước của toà nhà (Hình 19).
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\) và \(AC\). Đường thẳng \(MN\) song song với mặt phẳng
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung. Kết luận nào sau đây đúng?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB.\) Gọi \(P,\,\,Q\) lần lượt là hai điểm nằm trên cạnh \(SA\) và \(SB\) sao cho \(\frac{{SP}}{{SA}} = \frac{{SQ}}{{SB}} = \frac{1}{3}\). Khẳng định nào sau đây là đúng?
