Một góc lượng giác \(\alpha \) có điểm cuối ở góc phần tư thứ II thì
Một góc lượng giác \(\alpha \) có điểm cuối ở góc phần tư thứ II thì
-
A.
\(\left| {\sin \alpha } \right| = - {\rm{sin}}\alpha \)
-
B.
\(\sqrt {{\rm{si}}{{\rm{n}}^2}\alpha } = {\rm{sin}}\alpha \)
-
C.
\(\sqrt {{\rm{co}}{{\rm{s}}^2}\alpha } = {\rm{cos}}\alpha \)
-
D.
\(\tan \alpha > 0\)
Dựa vào đường tròn lượng giác để xét dấu \(\sin \alpha \) và \(\cos \alpha \).
Một góc lượng giác \(\alpha \) có điểm cuối ở góc phần tư thứ II thì \(\sin \alpha > 0\), \(\cos \alpha < 0\).
Đáp án : B

Các bài tập cùng chuyên đề
Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4}\)và \({420^ \circ }\)
Trong mặt phẳng tọa độ vẽ đường tròn tâm O bán kính R = 1. Chọn điểm gốc của đường tròn là giao điểm của đường tròn với trục . Ta quy ước chiều dương của đường tròn là chiều ngược chiều quay của kim đồng hồ và chiều âm là chiều quay của kim đồng hồ.
a) Xác định điểm trên đường tròn sao cho sđ\((OA,OM) = \frac{{5\pi }}{4}\)
b) Xác định điểm trên đường tròn sao cho sđ\((OA,ON) = - \frac{{7\pi }}{4}\)
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
a) \(\frac{{2\pi }}{3}\); b) \( - \frac{{11\pi }}{4}\); c) \({150^0}\); d) \( - {225^0}\).
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\;\beta = \frac{\pi }{3},\;\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{3}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
A. \(\beta \) và \( \gamma \)
B. \(\alpha, \beta, \gamma \)
C. \(\beta ,\gamma ,\delta \)
D. \(\alpha \) và \(\beta \),
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\;\beta = \frac{\pi }{3},\;\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{3}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
A. \(\beta \) và \( \gamma \)
B. \(\alpha, \beta, \gamma \)
C. \(\beta ,\gamma ,\delta \)
D. \(\alpha \) và \(\beta \),
Xác định điểm N trên đường tròn lượng giác sao cho \(\left( {OA,ON} \right) = - \frac{\pi }{3}\)
a) Trong mặt phẳng tọa độ (định hướng) Oxy, hãy vẽ đường tròn tâm O và bán kính bằng 1
b) Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) \( - {1485^ \circ }\)
b) \(\frac{{19\pi }}{4}\)
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là \(\pi \,\) và \( - \frac{\pi }{2}\)
Góc lượng giác \(\frac{{31\pi }}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\(\frac{{3\pi }}{7};\,\,\frac{{10\pi }}{7};\,\,\frac{{ - 25\pi }}{7}\)
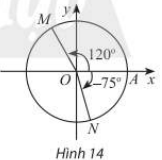
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14:
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).

Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:
a) \(\frac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\).
b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\).
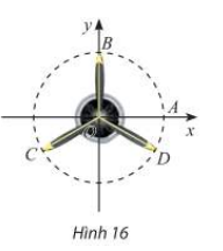
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a) \(\frac{{ - 17\pi }}{3}\)
b) \(\frac{{13\pi }}{4}\)
c) \( - 765^\circ \)
-
A.
Thứ II
-
B.
Thứ IV
-
C.
Thứ II hoặc IV
-
D.
Thứ I hoặc III
Trong mặt phẳng tọa độ \(Oxy,\) cho đường tròn lượng giác như hình vẽ bên dưới.
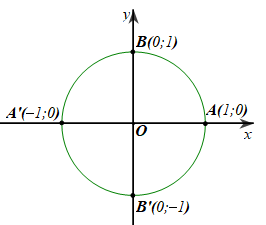
Hỏi góc lượng giác nào sau đây có số đo là \( - 90^\circ \)?
-
A.
\(\left( {OA,OB} \right)\)
-
B.
\(\left( {OA,OA'} \right)\)
-
C.
\(\left( {OA,OB'} \right)\)
-
D.
\(\left( {OA,OA} \right)\)
Cho $\alpha $ thuộc góc phần phần tư thứ nhất của đường tròn lượng giác. Khẳng định nào sau đây là đúng?
-
A.
$\sin \alpha > 0$
-
B.
$\cos \alpha < 0$
-
C.
$\tan \alpha < 0$
-
D.
$\cot \alpha < 0$
Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau
a) \(\frac{\pi }{6}\);
b) \(\frac{{ - 5\pi }}{7}\);
c) \({270^0}\);
d) \( - {415^0}\).
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng:
a) \(\frac{{23\pi }}{4}\);
b) \(\frac{{31\pi }}{6}\);
c) \( - {1380^0}\).
Trên đường tròn lượng giác lấy điểm \(M\) sao cho \(\left( {OA,OM} \right) = {40^o}\). Gọi \(M'\) là điểm đối xứng với \(M\) qua gốc toạ độ. Khi đó số đo của góc lượng giác \(\left( {OA,OM'} \right)\) bằng:
A. \({40^o} + k{360^o}\)
B. \({140^o} + k{360^o}\)
C. \({220^o} + k{360^o}\)
D. \({50^o} + k{360^o}\)
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a) \( - {1965^0}\);
b) \(\frac{{48\pi }}{5}\).
a) Góc lượng giác \( - {245^0}\) có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\( - {605^0}, - {65^0},{115^0},{205^0},{475^0}\).
b) Góc lượng giác \(\frac{{24\pi }}{5}\) có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\( - \frac{{16\pi }}{5}; - \frac{\pi }{5};\frac{{14\pi }}{5};\frac{{29\pi }}{5};\frac{{53\pi }}{{10}}\).
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng là:
a) \(\frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\);
b) \(\frac{\pi }{4} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\).
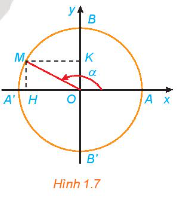
Trong hình bên, các điểm M, A’, N tạo thành ba đỉnh của một tam giác đều. Vị trí các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác nào sau đây?
\(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right); - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right); - \frac{\pi }{3} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\).
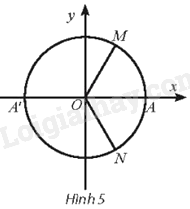
Cho ba điểm M, N, P lần lượt là các điểm biểu diễn trên đường tròn lượng giác của các góc lượng giác có số đo \(k2\pi ,\frac{\pi }{2} + k2\pi ,\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\). Tam giác MNP là tam giác gì?
Điểm biểu diễn trên đường tròn lượng giác của góc lượng giác có số đo \( - {830^0}\) thuộc góc phần tư thứ mấy?
A. Góc phần tư thứ I.
B. Góc phần tư thứ II.
C. Góc phần tư thứ III.
D. Góc phần tư thứ IV.
Điểm cuối của góc lượng giác $\alpha $ ở góc phần tư phần thứ mấy nếu $\sqrt {{{\sin }^2}\alpha } = \sin \alpha $.
-
A.
Thứ III.
-
B.
Thứ I hoặc III.
-
C.
Thứ I hoặc II.
-
D.
Thứ III hoặc IV.
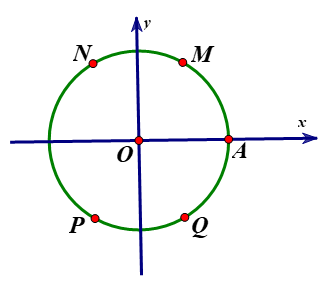
Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác như hình vẽ bên dưới. Điểm nào trong bốn đáp án A, B, C, D biểu diễn cho góc lượng giác có số đo bằng $60^\circ ?$
-
A.
Điểm $N.$
-
B.
Điểm $M.$
-
C.
Điểm $P.$
-
D.
Điểm $Q.$
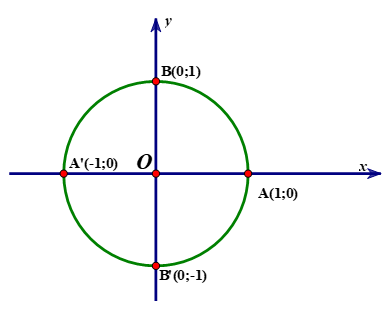
Trong mặt phẳng tọa độ $Oxy,$cho đường tròn lượng giác như hình vẽ bên dưới. Hỏi góc lượng giác nào sau đây có số đo là $90^\circ ?$
-
A.
$\left( {OA,\,\,OB'} \right).$
-
B.
$\left( {OA,\,\,OA} \right).$
-
C.
$\left( {OA,\,\,OB} \right).$
-
D.
$\left( {OA,\,\,OA'} \right).$







Danh sách bình luận