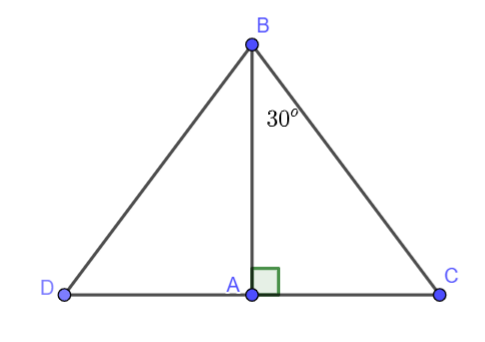
Cho tam giác MBC vuông tại M có \(\widehat B = {60^o}\). Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
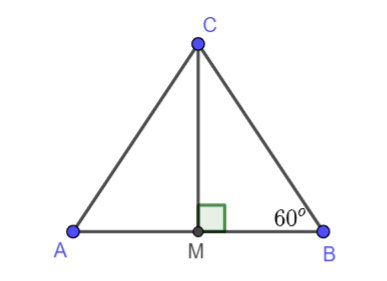
Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
|
GT |
\(\Delta MBC,\widehat M = {90^o},\widehat B = {60^o},MA = MB\) A thuộc tia đối của tia MB |
|
KL |
\(\Delta ABC\)đều. |
Ta thấy hai tam giác MBC và MAC vuông tại M và có:
MB = MA (theo giả thiết)
MC là cạnh chung
Vậy \(\Delta MBC = \Delta MAC\)(hai cạnh góc vuông). Do đó \(\widehat A = \widehat B = {60^o}\)
Suy ra \(\widehat C = {180^o} - \widehat A - \widehat B = {60^o}\)
Vậy ABC là tam giác có ba góc bằng nhau nên đây là tam giác đều.

Các bài tập cùng chuyên đề
Cho tam giác MBC vuông tại M có \(\widehat B\) = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
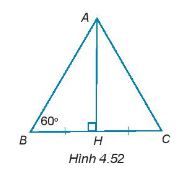
Cho tam giác ABH vuông tại đỉnh H có \(\widehat {ABH} = {60^0}\). Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng \(\Delta ABC\) là tam giác đều và \(BH = \dfrac{{AB}}{2}\)
Trong các câu sau đây, câu nào đúng?
A. Tam giác có ba cạnh bằng nhau là tam giác đều.
B. Tam giác có hai góc bằng nhau là tam giác đều.
C. Tam giác nhọn có hai cạnh bằng nhau là tam giác đều.
D. Tam giác vuông có một góc có số đo bằng 60 độ là tam giác đều.
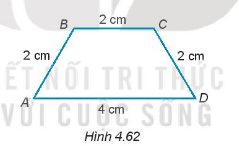
Cho hình thang cân ABCD có đáy lớn AD đáy nhỏ BC thoả mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.
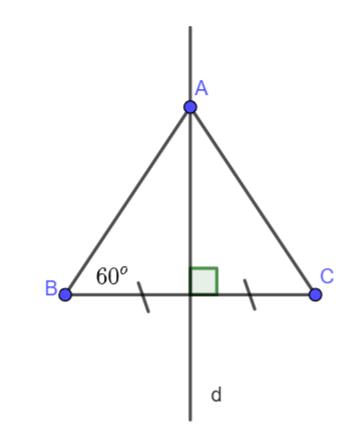
Cho điểm A nằm trên trung trực của đoạn thẳng BC sao cho \(\widehat {ABC} = {60^o}\). Chứng minh rằng CA = CB.
Tam giác ABC vuông tại đỉnh A và có \(\widehat B = {30^o}\). Chứng minh rằng BC = 2AC
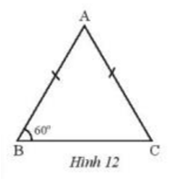
Cho tam giác ABC cân tại A có góc B bằng \({60^o}\). Chứng minh rằng tam giác ABC đều.
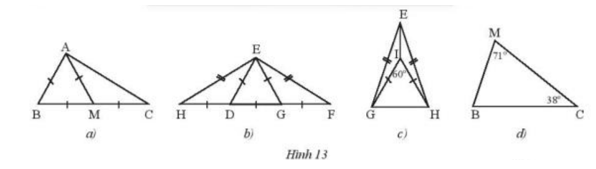
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.
Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:
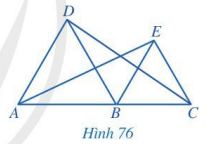
a) AD // BE và BD // CE;
b) \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);
c) AE = CD.
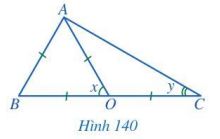
Tìm các số đo x, y trong Hình 140.
Cho tam giác đều ABC. Gọi E, D, F là ba điểm lần lượt nằm trên ba cạnh AB, AC, BC sao cho AD = CF = BE. Chứng minh tam giác DEF là tam giác đều.







Danh sách bình luận