Ta gọi hai góc có tổng bằng 180° là hai góc bù nhau. Hãy viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: “Hai góc cùng bù một góc thứ ba thì hai góc đó bằng nhau”.
Viết giả thiết và kết luận bằng kí hiệu:
Chứng minh định lí:
Theo GT ta có:
\(\widehat A\) bù với \(\widehat C\) nên \(\widehat A\)+\(\widehat C\)=180°
Suy ra \(\widehat A\)=180° − \(\widehat C\) (1)
\(\widehat B\) bù với \(\widehat C\) nên \(\widehat B+\widehat C\)=180°
Suy ra \(\widehat B\)=180° − \(\widehat C\) (2)
Từ (1) và (2) suy ra \(\widehat A\)=\(\widehat B\)
Vậy \(\widehat A\)=\(\widehat B\)
Các bài tập cùng chuyên đề
Tìm tổng số đo của góc 110 \(^\circ \) và 70 \(^\circ \)
Hai góc bù nhau là hai góc có tổng số đo bằng:
-
A.
\(90^{o}\);
-
B.
\(180^{o}\);
-
C.
\(360^{o}\);
-
D.
\(120^{o}\).
Cho hình vẽ. Biết góc \(GFI\) và góc \(FIH\) là hai góc bù nhau.
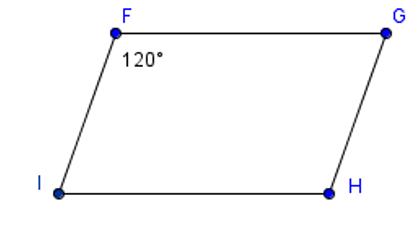
Số đo góc \(FIH\) là
-
A.
\(120^{o}\);
-
B.
\(80^{o}\);
-
C.
\(60^{o}\);
-
D.
\(90^{o}\).
Quan sát hình vẽ sau và cho biết:
Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\) có bù với nhau không? Vì sao?
-
A.
Hai góc có một cạnh chung;
-
B.
Hai góc có tổng bằng \(180^{o}\);
-
C.
Hai góc có một cạnh chung và có tổng bằng \(180^{o}\);
-
D.
Hai góc có một cạnh chung và hai cạnh còn lại là hai tia đối nhau.
