Cho Hình 11
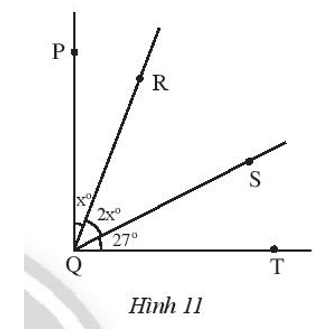
a) Tìm các góc kề với \(\widehat {RQS}\)
b) Cho biết \(\widehat {PQT}\)=90°. Tìm số đo của các góc \(\widehat {RQS}\) và \(\widehat {RQP}\)
Ta sử dụng định nghĩa về 2 góc kề nhau và tính chất các góc phụ nhau để tìm x
a) Các góc kề với \(\widehat {RQS}\) là: \(\widehat {PQR}\) và \(\widehat {SQT}\)
b) Vì \(\widehat {RQS}\) kề với \(\widehat {PQR}\) và \(\widehat {SQT}\)nên ta có:
\(\widehat {RQS} + \widehat {PQR} + \widehat {SQT} = \widehat {PQT}\)
Hay x° + 2x° + 27° = 90°
Suy ra 3x° = 63°
Do đó x° = 21°.
Suy ra 2x° = 2.21° = 42°.
Vậy \(\widehat {RQS}\) = 2x° = 42° và \(\widehat {PQR}\) = x° = 21°.

Các bài tập cùng chuyên đề
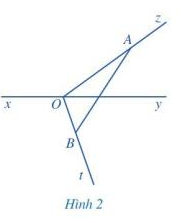
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
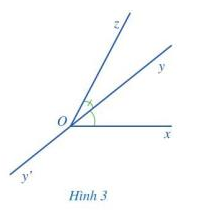
Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
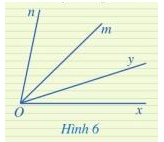
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
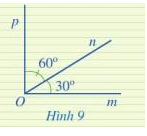
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
Quan sát Hình 11. Tính số đo mỗi góc xOy, yOz biết \(\dfrac{1}{5}\widehat {xOz} = \dfrac{1}{4}\widehat {yOz}\).
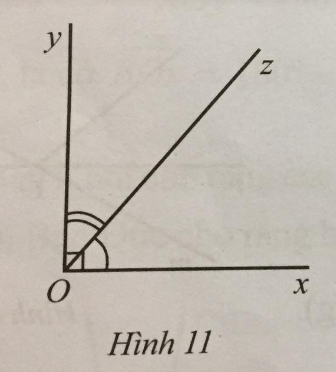
Cho hình vẽ sau:
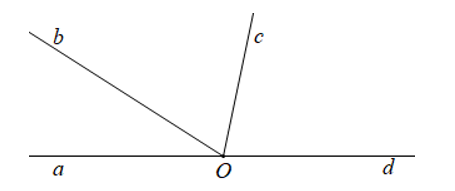
Số cặp góc kề bù (không kể góc bẹt) có trong hình vẽ trên là
-
A.
1;
-
B.
2;
-
C.
3;
-
D.
4.
Hãy kể tên các cặp góc kề nhau trong hình vẽ dưới đây.
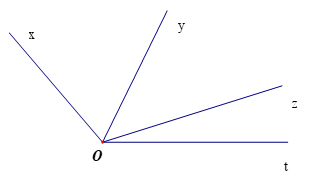
Tìm số đo của góc \(\widehat {xOz}\), biết \(\widehat {xOy} = 70^{o}\) và \(\widehat {yOz} = 55^{o}\).
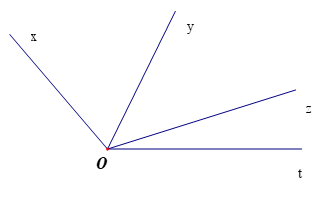
Hai góc kề nhau là hai góc
-
A.
có chung đỉnh;
-
B.
có một cạnh chung;
-
C.
có hai cạnh nằm về hai phía của đường thẳng chứa cạnh chung;
-
D.
Cả A, B và C.
Cho hình vẽ:
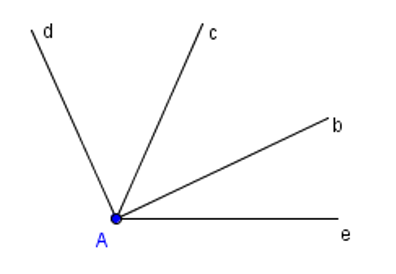
Khẳng định đúng là
-
A.
Góc \(dAc\) và góc \(bAe\) là hai góc kề nhau;
-
B.
Góc \(dAc\) và góc \(cAe\) là hai góc kề nhau;
-
C.
Góc \(dAc\) và góc \(dAb\) là hai góc kề nhau;
-
D.
Góc \(dAc\) và góc \(dAe\) là hai góc kề nhau.
Cho hình vẽ. Biết góc \(xOy\) có số đo là \(80^{o}\), góc \(yOz\) có số đo là \(40^{o}\). Số đo góc \(xOz\) là
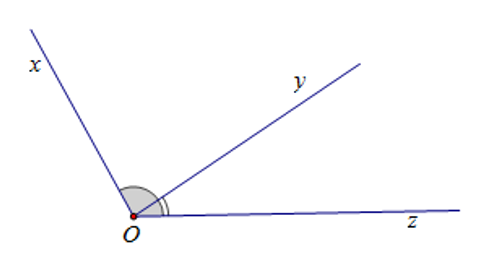
-
A.
\(120^{o}\);
-
B.
\(40^{o}\);
-
C.
\(160^{o}\);
-
D.
\(80^{o}\);
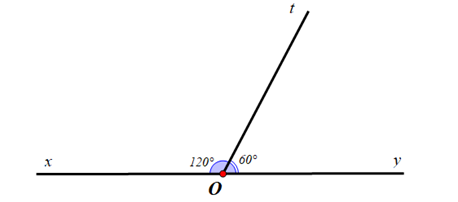
Trong các hình dưới đây hình nào không chứa hai góc kề nhau.
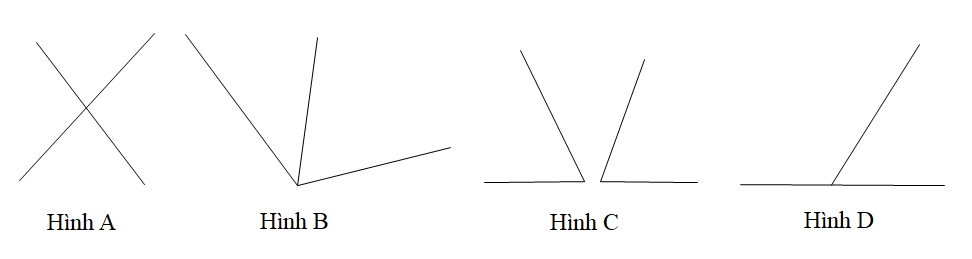
-
A.
Hình A;
-
B.
Hình B;
-
C.
Hình C;
-
D.
Hình D.
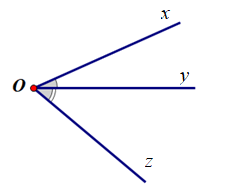
Quan sát hình vẽ sau và cho biết:
Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\) có kề với nhau không? Vì sao?
-
A.
 ;
; -
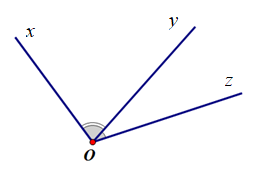
B.
 ;
; -
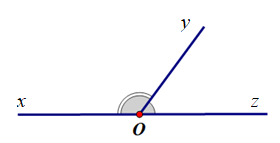
C.
 ;
; -
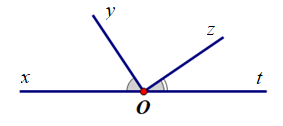
D.
 .
.







Danh sách bình luận