Cho hình thoi \(ABCD\) có góc \(B\) tù. Kẻ \(BE\) vuông góc \(AD\) tại \(E\), \(BF\) vuông góc với \(CD\) tại \(F\). Gọi \(M,N\) lần lượt là giao điểm của \(BE,BF\) với \(AC\). Chứng minh tứ giác \(BMDN\) là hình thoi.
Dựa vào tính chất của hình thoi:
Trong một hình thoi:
- Các cạnh đối song song
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
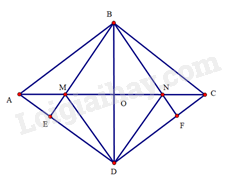
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
Do \(ABCD\) là hình thoi nên \(AC\) vuông góc với \(BD\) tại trung điểm \(O\) của \(BD\). Suy ra \(AC\) là đường trung trực của \(BD\). Do đó \(BM = DM,BN = DN\).
Do \(ABCD\) là hình thoi nên \(BA = BC,\widehat {BAE} = \widehat {BCF}\).
Suy ra \(\Delta ABE = \Delta BCF\) (cạnh huyền – góc nhọn kề)
Do đó \(\widehat {ABE} = \widehat {CBF}\). Mà \(\widehat {ABD} = \widehat {CBD}\), suy ra \(\widehat {MBO} = \widehat {NBO}\).
\(\Delta MBO = \Delta NBO\) (cạnh góc vuông – góc nhọn). suy ra \(BM = BN\)
Mà \(BM = DM\) và \(BN = DN\), suy ra \(BM = DM = BN = DN\).
Tứ giác \(BMDN\) có \(BM = DM = BN = DN\) nên \(BMDN\) là hình thoi.
Các bài tập cùng chuyên đề
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi \(ABCD\) có \(O\) là giao điểm của hai đường chéo (Hình 13b). Các tam giác \(OAB\), \(OCB\), \(OCD\), \(OAD\) có bằng nhau không?
Cho hình thoi \(MNPQ\) có \(I\) là giao điểm của hai đường chéo.
a) Tính \(MP\) khi biết \(MN = 10\)dm, \(IN = 6\)dm
b) Tính \(\widehat {{\rm{IMN}}}\) khi \(\widehat {{\rm{MNP}}} = 128^\circ \)
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là ${3,2}$cm và ${2,4}$cm.
Cho hình thoi \(ABCD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Biết \(AC = 6\)cm; \(BD = 8\)cm. Tính độ dài cạnh của hình thoi \(ABCD\)
Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60cm và 80cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều, Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:
A. 5m
B. 1m
C. 1,5m
D. 2m
Cho hình thoi \(ABCD\) có cạnh bằng \(13\)cm, độ dài đường chéo \(AC\) là 10cm. Độ dài đường chéo \(BD\) là:
A. 24cm
B. 12cm
C. 16cm
D. 20cm
Họa tiết trên vải ở Hình 55 gợi lên hình ảnh của hình thoi.
Hình thoi có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình thoi?
Cho hình thoi ABCD có hai đường chéo là AC và BD cắt nhau tại O (hình 58)
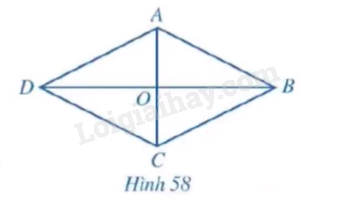
a) Hình thoi ABCD có là hình bình hành hay không?
b) Hai đường chéo AC và BD có vuông góc với nhau hay không?
c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay không?
Cho hình thoi ABCD có \(\widehat {ABC} = {120^o}\). Chứng minh tam giác ABD là tam giác đều.
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:
\(A{C^2} + B{{\rm{D}}^2} = 4\left( {O{A^2} + O{B^2}} \right) = 4{\rm{A}}{B^2}\)
Cho hình thoi ABCD có \(\widehat {C{\rm{D}}B} = {40^o}\). Tính số đo mỗi góc của hình thoi ABCD.
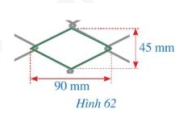
Hình 62 mô tả một ô lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mmm và 90 mm. Độ dài cạnh của ô lưới mắt đó là bao nhiêu milimét (làm tròn kết quả đến hàng đơn vị)?
Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là \({60^o}\) (Hình 63).
Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm).
Cho hình thoi \(ABCD\) (Hình 3.66).
a) Tam giác \(ABC\) là tam giác gì?
b) Vì sao \(BO\) là đường trung tuyến của tam giác \(ABC\)?
c) Em rút ra thêm được tính chất gì về hai đường chéo của hình thoi?
Hình thoi \(MNPQ\) có \(\widehat {NMQ} = 124^\circ \). Tính số đo góc \(MNQ\).
Cho hình thoi \(ABCD\). Hãy tìm độ dài thích hợp cho các ô ? trong bảng dưới đây:
Cho một hình thoi có độ dài hai đường chéo là \(\frac{{18}}{5}\) m và \(\frac{{27}}{{10}}\) m. Tính chu vi và diện tích của hình thoi đó.
Cho hình thoi \(ABCD\) có \(AB = 2\)cm, \(\widehat A = \frac{1}{2}\widehat B\). Các điểm \(H,K\) thay đổi lần lượt trên cạnh \(AD,CD\) sao cho \(\widehat {HBK} = 60^\circ \).
a) Chứng minh \(DH + DK\) không đổi
b) Xác định vị trí của các điểm \(H,K\) để độ dài \(HK\) ngắn nhất. Tính độ dài ngắn nhất đó.
Hình thoi không có tính chất nào dưới đây?
