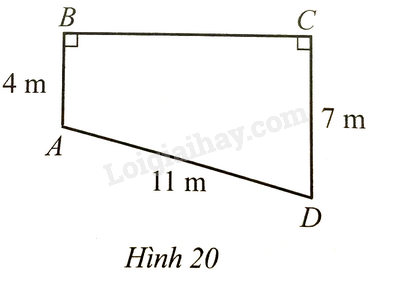
Hình 20 mô tả mặt phẳng cắt ngang tầng trệt của một ngôi nhà. Biết \(AB \bot BC,CD \bot BC\) và \(AB = 4m,CD = 7m,AD = 11m\). Tính độ dài \(BC\) (làm tròn kết quả đến hàng phần mười của mét).
Dựa vào tính chất của hình chữ nhật:
- Hai cạnh đối song song và bằng nhau
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
Và dựa vào định lí Pythagore: trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
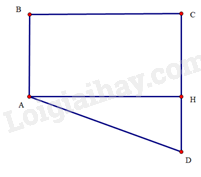
Kẻ \(AH\) vuông góc với \(CD\) tại \(H\) (Hình 42)
Tứ giác \(ABCH\) có \(\widehat {ABC} = \widehat {BCH} = \widehat {CHA} = 90^\circ \) nên \(ABCH\) là hình chữ nhật. Suy ra \(CH = AB = 4m\)
Do đó \(DH = CD - CH = 3m\)
Trong tam giác \(ADH\) vuông tại \(H\), ta có:
\(A{D^2} = A{H^2} + D{H^2}\)
Suy ra \(A{H^2} = A{D^2} - D{H^2} = 112\)
Do đó \(AH = \sqrt {112} m\)
Ta có: \(BC = AH\) (vì \(ABCH\) là hình chữ nhật) nên \(BC = \sqrt {112} \approx 10,6\left( m \right)\)
Các bài tập cùng chuyên đề
Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Ta có tính chất sau đây về đường chéo của hình chữ nhật.
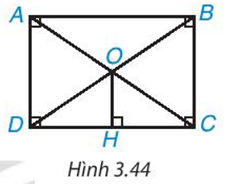
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
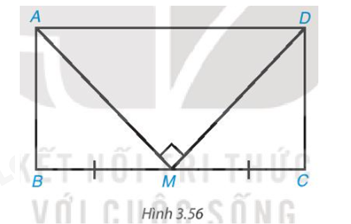
Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56).
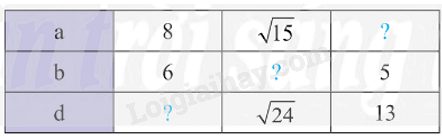
Dùng thước đo góc để đo số đo các góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) ở Hình 1 và rút ra nhận xét và số đo của chúng.
Cho \(ABCD\) là hình chữ nhật.
a) Chứng minh \(AB\) // \(CD\) và \(AD\) // \(BC\)
b) Tam giác \(ABD\) và tam giác \(BAC\) có bằng nhau không? Vì sao?
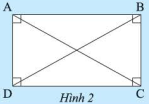
Cho biết \(a\), \(b\), \(d\) lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.
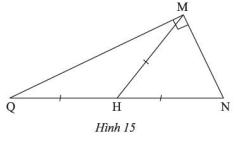
Cho Hình 15. Vẽ thêm điểm \(P\) để tứ giác \(MNPQ\) là hình chữ nhật
Màn hình phẳng của chiếc ti vi ở Hình 46 có dạng hình chữ nhật
Hình chữ nhật có những tính chất gì? Có những dấu hiệu nào để nhận biết một hình bình hành là hình chữ nhật?
a) Mỗi hình chữ nhật có là một hình thang cân hay không?
b) Mỗi hình chữ nhật có là một hình bình hành hay không?
Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây:
A. NQ
B. MN
C. NP
D. QM
Từ các tính chất về cạnh và đường chéo của hình bình hành và hình thang cân, em có thể suy ra những tính chất gì về cạnh và đường chéo của hình chữ nhật?
Hình chữ nhật MNPQ có hai đường chéo cắt nhau tại I và \(MP = 4cm.\) Tính độ dài IQ.
Cho hình chữ nhật ABCD có hai đường chéo cắt nhau tại O. Chọn phương án đúng.
A. AB = DC, AD = BC, AB ⊥ DC.
B. AB // DC, AD // BC, AB = AC.
C. \(\hat B = 90^\circ ,\hat C = 90^\circ ,\widehat {AOD} = 90^\circ \).
D. OA = OB = OC = OD.
Cho hình chữ nhật ABCD. Gọi O là trung điểm của AC. Hạ OM vuông góc với BC tại M, ON vuông góc với BC tại N.
a) Chứng minh \(OA = \frac{1}{2}BD.\)
b) Chứng minh MN = OC.
c) Kẻ BK vuông góc với AC tại K, OM giao với BK tại H. Chứng minh CH vuông góc với OB.
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
Khẳng định nào sau đây là sai?
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\)
Cho hình chữ nhật \(ABCD\). \(E, F, G, H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\parallel AC\), \(GH\parallel AC\), \(EH\parallel BD\), \(FG\parallel BD\). Tứ giác \(EFGH\) là hình gì?
