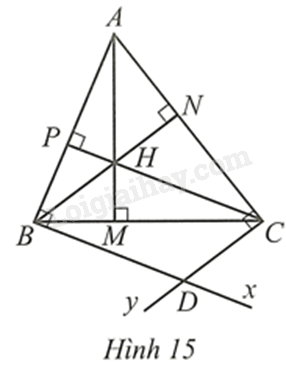
Cho tam giác nhọn \(ABC\) có ba đường cao \(AM,BN,CP\) cắt nhau tại \(H\). Qua \(B\) kẻ tia \(Bx\) vuông góc với \(AB\). Qua \(C\) kẻ tia \(Cy\) vuông góc với \(AC\). Gọi \(D\) là giao điểm của \(Bx\) và \(Cy\) (Hình 15)
a) Chứng minh tứ giác \(BDCH\) là hình bình hành;
b) Tam giác \(ABC\) có điều kiện gì thi ba điểm \(A,D,H\) thẳng hàng?
c) Tìm mối liên hệ giữa góc \(A\) và góc \(D\) của tứ giác \(ABCD\).
d) Giả sử \(H\) là trung điểm của \(AM\). Chứng minh diện tích của tam giác \(ABC\) bằng diện tích của tứ giác \(BHCD\).
Dựa vào dấu hiệu nhận biết của hình bình hành:
- Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
- Tứ giác có hai cặp góc đối bằng nhau là hình bình hành
- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
a) Ta có: \(\widehat {APC} = \widehat {ABD} = 90^\circ \) và \(\widehat {APC},\widehat {ABD}\) nằm ở vị trí đồng vị nên \(CP//BD\).
Tương tự ta chứng minh được \(BN//CD\).
Tứ giác \(BDCH\) có \(BD//CH,BH//CD\) nên \(BDCH\) là hình bình hành.
b) Để ba điểm \(A,D,H\) thẳng hàng thì \(M\) phải thuộc \(DH\). Mà \(M\) thuộc \(BC\), suy ra \(M\) là giao điểm của \(BC\) và \(DH\).
Do \(BDCH\) là hình bình hành nên hai đường chéo \(BC\) và \(DH\) cắt nhau tại trung điểm của mỗi đường. suy ra \(M\) là trung điểm \(BC\).
Khi đó \(\Delta ABM = \Delta ACM\) (c.g.c). Suy ra \(AB = AC\).
Dễ thấy nếu tam giác \(ABC\) có \(AB = AC\) thì ba điểm \(A,D,H\) thẳng hàng.
Vậy tam giác \(ABC\) cân tại \(A\) thì \(A,D,H\) thẳng hàng.
c) Xét tứ giác \(ABCD\), ta có: \(\widehat {BAC} + \widehat {DBA} + \widehat {CDB} + \widehat {ACD} = 360^\circ \).
Mà \(\widehat {DBA} = \widehat {ACD} = 90^\circ \), suy ra tính được \(\widehat {BAC} + \widehat {CDB} = 3180^\circ \)
Vậy góc \(A\) và góc \(D\)của tứ giác \(ABCD\) là hai góc bù nhau.
d) Do \(H\) là trung điểm của \(AM\) nên \(HM = \frac{1}{2}AM\)
Ta có diện tích tam giác \(ABC\) bằng: \(\frac{1}{2}.AM.BC = HM.BC\).
Ta chứng minh được \(\Delta BCH = \Delta CBD\) (c.c.c.). Suy ra diện tích tứ giác \(BHCD\) bằng 2 lần diện tích tam giác \(BCH\).
Do đó, diện tích tứ giác \(BHCD\) bằng: \(\left( {\frac{1}{2}.HM.BC = HM.BC} \right)\) vạy diện tích tam giác \(ABC\) bằng điệnt tích của tứ giác \(BHCD\).

Các bài tập cùng chuyên đề
Hãy viết giả thiết, kết luận của Định lí 2.
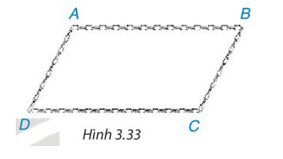
Chia một sợi dây xích thành bốn đoạn: hai đoạn dài bằng nhau, hai đoạn ngắn bằng nhau và đoạn dài, đoạn ngắn xen kẽ nhau. Hỏi khi móc hai đầu mút của sợi dây xích đó lại để được một tứ giác ABCD (có các đỉnh tại các điểm chia) như Hình 3.33 thì tứ giác ABCD là hình gì? Tại sao?
Hãy biết giả thiết, kết luận của Định lí 3.
Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A’, B’ là các điểm sao cho O là trung điểm của AA’, BB’. Chứng minh rằng A’B’ = AB và đường thẳng A’B’ song song với đường thẳng AB.
Trở lại bài toán mở đầu. Em hãy vẽ hình và nêu cách vẽ con đường cần mở đi qua O sao cho theo con đường đó, hai đoạn đường từ O tới a và tới b bằng nhau.
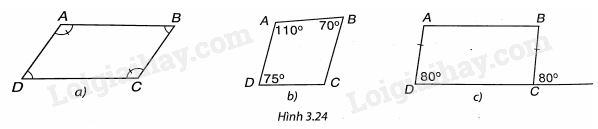
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?
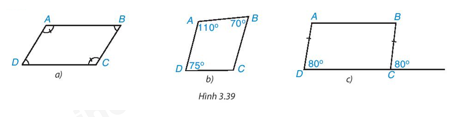
Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
Vẽ tứ giác ABCD theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.
Bước 2. Lấy điểm C ∈ a.
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.
b) Hỏi tìm được bao nhiêu điểm như vậy?
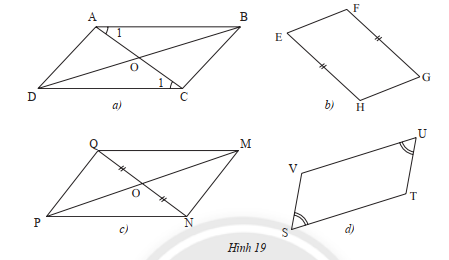
Cho tứ giác \(ABCD\) có \(P\) là giao điểm của hai đường chéo. Giải thích tại sao \(AB\) // \(CD\) và \(AD\) // \(BC\) trong mỗi trường hợp sau:
Trường hợp 1: \(AB = CD\) và \(AD = BC\) (Hình 7a)
Trường hợp 2: \(AB\) // \(CD\) và \(AB = CD\) (Hình 7b)
Trường hợp 3: \(AD\) // \(BC\) và \(AD = BC\) (Hình 7c)
Trường hợp 4: \(\widehat {\rm{A}} = \widehat {\rm{C}}\), \(\widehat {\rm{B}} = \widehat {\rm{D}}\) (Hình 7d)
Trường hợp 5: \(PA = PC\), \(PB = PD\) (Hình 7e)
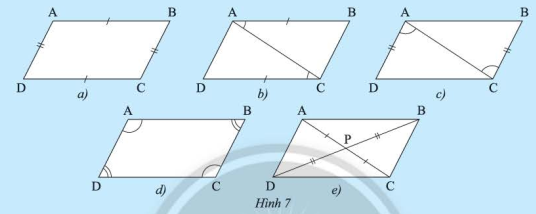
Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?
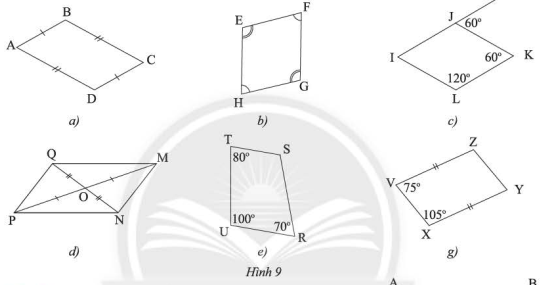
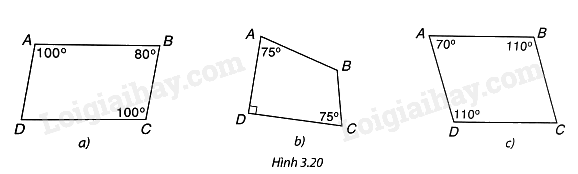
Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành một hình bình hành?
Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\)
a) Chứng minh rằng tứ giác \(EBFD\) là hình bình hành
b) Gọi \(O\) là giao điểm của hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng ba điểm \(E\), \(O\), \(F\) thẳng hàng.
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn: OA = OC và \(\widehat {OA{\rm{D}}} = \widehat {OCB}\). Chứng minh tứ giác ABCD là hình bình hành.
a) Cho tứ giác ABCD có AB = CD, BC = DA (hình 39)
- Hai tam giác ABC và CDA có bằng nhau hay không?
Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CAD}\).
ABCD có phải là hình bình hành hay không?
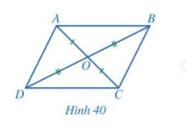
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40)
Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CA{\rm{D}}}\).
ABCD có phải là hình bình hành hay không?
Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.
Cho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\). Chứng minh ABCD là hình bình hành.
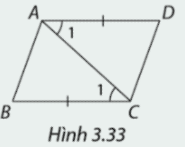
Trong mỗi trường hợp ở hình 3.33, em hãy giải thích vì sao các tam giác được cho bằng nhau và ABCD là hình bình hành.
a)
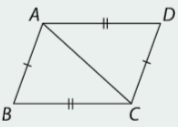
b) \(\Delta ABC = \Delta CDA.\)
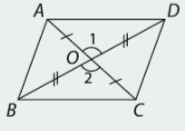
c) \(\Delta {\rm{OAD = }}\Delta {\rm{OCB}}\)
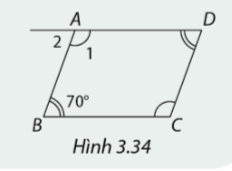
Trong hình 3.34, tứ giác \(ABCD\) có \(\widehat {{A_1}} = \widehat C\) và \(\widehat B = \widehat D = 70^\circ .\)
Em hãy tính số đo các góc \({A_1},{A_2}\) và giải thích vì sao \(ABCD\) là hình bình hành.
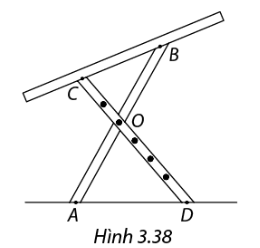
Trong các tứ giác ở hình 3.35, tứ giác nào là hình bình hành?
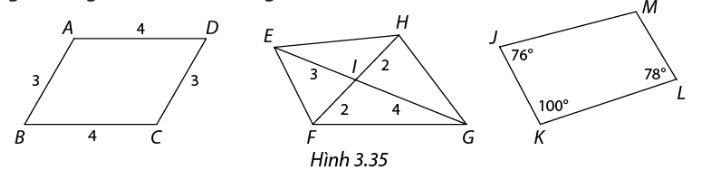
Trong Hình 3.37, AC và BD là đường kính của hai đường tròn có cùng tâm O. Khi các điểm A, B, C, D không thẳng hàng, tứ giác ABCD là hình gì? Vì sao?
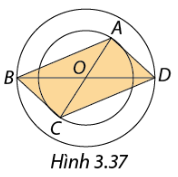
Bàn vẽ có hai chân AB và CD được gắn với nhau theo hình chữ X tại trung điểm O của chân AB. Điểm O có thể di chuyển dọc theo chân bàn CD để điều chỉnh độ nghiêng của mặt bàn (Hình 3.38). Điểm O ở vị trí nào trên đoạn thẳng CD thì cạnh bàn BC song song với đường thẳng AD trên mặt đất? Khi đó ABCD là hình gì?
Điền cụm từ thích hợp vào chỗ trống.
a) Tứ giác có các ............. đối ............................................ là một hình bình hành.
b) Tứ giác có ............................................. song song và .................................................. là một hình bình hành.
c) Trong hình bình hành, hai góc kề ................. bất kì có ...................... bằng 180°.
d) Tứ giác có ............................................... cắt nhau tại ........................................ của mỗi đường là hình bình hành.
e) Tứ giác có các góc ........................................... là một hình bình hành.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?
Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.
Trong các tứ giác ở Hình 3.24, tứ giác nào là hình bình hành? Vì sao?
Chứng minh rằng nếu hai góc kề của mỗi cạnh của một tứ giác đều là hai góc bù nhau thì tứ giác đó là một hình bình hành.
Cho hình thang ABCD với hai đáy AB, CD. Gọi K là trung điểm của BC. Lấy điểm A’, D’ sao cho K và trung điểm của AA’ và DD’. Hỏi tứ giác AD’A’D là hình gì? Vì sao?









Danh sách bình luận