Một người đứng cách gốc cây 20m nhìn thấy ngọn cây với góc \({36^o}\) so với phương nằm ngang. Biết mắt người ấy cách mặt đất 1,7m và cây mọc thẳng đứng (H.4.21a). Tính chiều cao của cây (làm tròn đến chữ số thập phân thứ nhất).
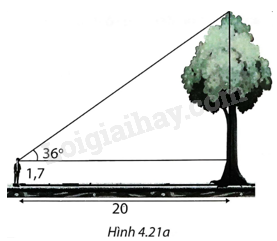
+ Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
+ Tam giác ABO vuông tại B nên \(OB = AB.\tan \widehat {BAO}\) nên tính được OB.
+ \(OH = BH + OB\), với \(BH = 1,7m\).
(H.4.21b)
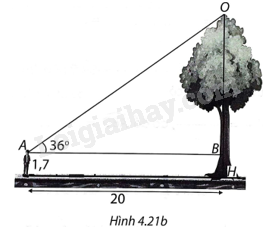
Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
Ta có \(AB = 20m\) và tam giác ABO vuông tại B.
Trong tam giác vuông ABO có
\(OB = AB.\tan \widehat {BAO} = 20.\tan {36^o} = 20.\sqrt {5 - 2\sqrt 5 } \approx 14,5\left( m \right)\)
Ta có: \(OH = OB + BH \approx 16,2\left( m \right)\)
Vậy cây cao khoảng 16,2m.

Các bài tập cùng chuyên đề
Một cột đèn có bóng trên mặt đất dài $7,5m.$ Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng ${42^0}.$ Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
-
A.
$6,753\,m$
-
B.
$6,75\,m$
-
C.
$6,751\,m$
-
D.
$6,755\,m$
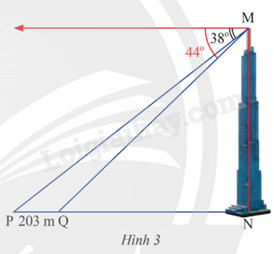
Hai điểm P và Q cách nhau 203 m và thẳng hàng với chân một tòa tháp (Hình 3). Từ đỉnh của tòa tháp đó, một người nhìn thấy hai điểm P, Q với hai góc nghiêng xuống lần lượt là \({38^o}\) và \({44^o}\). Tính chiều cao của tòa tháp (kết quả làm tròn đến hàng đơn vị của mét).
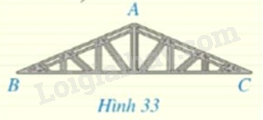
Mặt cắt đứng của khung thép có dạng tam giác cân \(ABC\) với \(\widehat B = 23^\circ ,AB = 4m\) (Hình 33). Tính độ dài đoạn thẳng \(BC\) (làm tròn kết quả đến hàng phần mười của mét).
Để ước lượng chiều cao của một cây trong sân trường, bạn Hoàng đứng ở sân trường (theo phương thẳng đứng), mặt bạn Hoàng đặt tại vị trí \(C\) cách mặt đất một khoảng \(CB = DH = 1,64m\) và cách cây một khoảng \(CD = BH = 6m\). Tính chiều cao \(AH\) của cây (làm tròn kết quả đến hàng phần trăm của mét), biết góc nhìn \(ACD\) bằng \(38^\circ \) minh họa ở Hình 36.

Trên mặt biển, khi khoảng cách \(AB\) từ ca nô đến chân tháp hải đăng là 250m, một người đứng trên tháp hải đăng đó nhìn về phía ca nô theo phương \(CA\) tạo với phương nằm ngang \(Cx\) một góc là \(\widehat {ACx} = 32^\circ \) (Hình 39). Tính chiều cao của tháp hải đăng (làm tròn kết quả đến hàng phần mười của mét), biết \(AB//Cx\) và độ cao từ tầm mắt của người đó đến đỉnh tháp là 3,2m.

Người ta kể lại rằng, vào thế kỉ XVI, nhà khoa học Galileo đã thả rơi các quả cầu cùng thể tích từ tháp nghiêng Pisa xuống mặt đất. Ông phát hiện ra hiện tượng lí thú rằng thời gian một vật rơi tự do không phụ thuộc vào cân nặng của vật đó (nguồn: https://www.britannica.com/summary/Galileo-Timeline). Biết chiều cao của tháp nghiêng Pisa ở phía thấp hơn là \(AH = 55,9m\) và góc nghiêng BAH của tháp so với phương thẳng đứng là khoảng \({4^o}\) (Hình 4.25), nếu thả một quả bóng từ vị trí A trên đỉnh tháp xuống đất thì bóng sẽ chạm đất cách điểm B ở chân tháp là bao nhiêu mét?

Cánh tay rô-bốt đặt trên mặt đất và có vị trí như Hình 4.28. Tính độ cao của điểm A trên đầu cánh tay rô-bốt so với mặt đất.
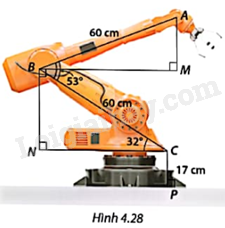
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
Trong Hình 4.29, một cánh diều được thả trên bầu trời với chiều dài dây là \(AD = 150m\), góc tạo bởi dây diều và phương nằm ngang là \(\widehat {DAH} = {40^o}\). Tính độ cao DH của cánh diều so với mặt đất.
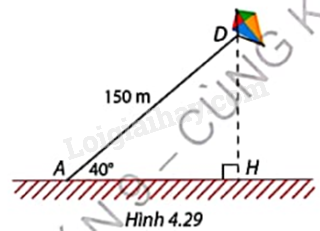
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
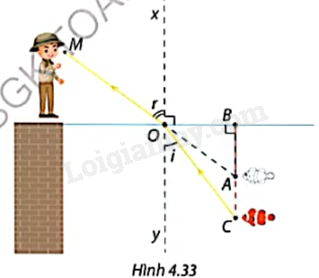
Khi tia sáng được truyền qua mặt phân cách giữa không khí và nước thì đường đi tia sáng sẽ bị lệch đi do hiện tượng khúc xạ ánh sáng. Góc tới i và góc khúc xạ r như Hình 4.33 liên hệ với nhau theo công thức \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\). Một con cá bơi ở vị trí C. Do ánh sáng bị khúc xạ nên Minh đứng trên bờ nhìn xuống nước với góc \(r = {54^o}\) thì thấy con cá ở vị trí A thẳng hàng với O, M và cách mặt nước một đoạn \(AB = 71cm\).
a) Tính góc tới i.
b) Tính độ sâu BC từ mặt nước đến vị trí thực sự mà con cá đang bơi.
Một cột đèn có bóng trên mặt đất dài \(6m.\) Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \({38^0}.\) Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(4,6\,m\)
-
B.
\(4,69\,m\)
-
C.
\(5,7\,m\)
-
D.
\(6,49\,m\)
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
Một cầu trượt trong công viên có độ dốc là \({25^0}\) và có độ cao là \(2,4m.\) Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(5,86\,m\)
-
B.
\(5\,m\)
-
C.
\(5,68\,m\)
-
D.
\(5,9\,m\)
Một cái cây bị sét đánh trúng thân cây làm thân cây ngả xuống đất, tạo với mặt đất một góc là ${40^0}$. Biết rằng khúc cây còn đứng cao $1\,m$ . Tính chiều cao lúc đầu của cây.
-
A.
$2,61\,m$
-
B.
$2,81\,m$
-
C.
$2,58\,m$
-
D.
$2,56\,m$
Một cái cây bị sét đánh trúng thân cây làm thân cây ngả xuống đất, tạo với mặt đất một góc là \({35^0}\) . Biết rằng khúc cây còn đứng cao \(1,5\,m\) . Tính chiều cao lúc đầu của cây. (làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(4\,m\)
-
B.
\(4,5\,m\)
-
C.
\(4,1\,m\)
-
D.
\(3,9\,m\)
Một chiếc máy bay đang bay lên với vận tốc $500\,km/h$ . Đường bay lên tạo với phương ngang một góc ${30^0}$. Hỏi sau $1,2$ phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu?
-
A.
$7\,km$
-
B.
$5\,km$
-
C.
$6\,km$
-
D.
$8\,km$
Một chiếc máy bay, đang bay lên với vận tốc \(480\,km/h\) . Đường bay lên tạo với phương ngang một góc \({25^0}\) .Hỏi sau \(1,5\) phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu? (làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(7,1\,km\)
-
B.
\(5\,km\)
-
C.
\(5,1\,km\)
-
D.
\(6\,km\)
Hai bạn học sinh Trung và Dũng đang đứng ở mặt đất bằng phẳng, cách nhau $100m$ thì nhìn thấy một chiếc diều ( ở vị trí $C$ giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Trung là ${50^0}$ và góc ''nâng'' để nhìn thấy diều ở vị trí của Dũng là ${40^0}$ . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
-
A.
$49,26\,m$
-
B.
$49,24\,m$
-
C.
$50\,m$
-
D.
$51\,m$
Hai bạn học sinh Mai và Đào đang đứng ở mặt đất bằng phẳng, cách nhau \(150m\) thì nhìn thấy một chiếc diều ( ở vị trí \(C\) giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Mai là \({45^0}\), góc ''nâng'' để nhìn thấy diều ở vị trí của Đào là \({35^0}\) . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(86\,m\)
-
B.
\(89\,m\)
-
C.
\(80\,m\)
-
D.
\(88,22\,m\)
Hai bạn học sinh $A$ và $B$ đang đứng ở mặt đất bằng phẳng, cách nhau 80 m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí $C$ nằm trên tia $AB$ và $AC>AB$). Biết góc ''nâng'' để nhìn thấy máy bay ở vị trí của $B$ là \(55^\circ \) góc ''nâng'' để nhìn thấy máy bay ở vị trí của $A$ là $40^\circ $. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
-
A.
$162,75\,m$
-
B.
$162,95\,m$
-
C.
$163,75\,m$
-
D.
$180\,m$
Hai bạn học sinh A và B đang đứng ở mặt đất bằng phẳng, cách nhau 60 m thì nhìn thấy một máy bay trực thăng điều khiển từ xa ( ở vị trí C nằm trên tia AB và AC>AB). Biết góc ''nâng'' để nhìn thấy máy bay ở vị trí của B là \(50^\circ \) và góc ''nâng'' để nhìn thấy máy bay ở vị trí của A là \(30^\circ .\) Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(67,91\,m\)
-
B.
\(69,17\,m\)
-
C.
\(67,19\,m\)
-
D.
\(134\,m\)
Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m (cùng 1 phía với ngọn núi), người ta nhìn thấy đỉnh núi với góc nắng lần lượt là \({34^o}\) và \({38^o}\).
-
A.
\(2368m\)
-
B.
\(1468m\)
-
C.
\(3468m\)
-
D.
\(2468m\)
Bạn Thanh đứng tại vị trí \(A\) cách cây thông \(6m\) và nhìn thấy ngọn của cây này dưới một góc bằng \({55^0}\) so với phương nằm ngang (như hình vẽ). Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng \(1,6m.\) Chiều cao \(BC\) của cây thông bằng (làm tròn đến số thập phân thứ hai):
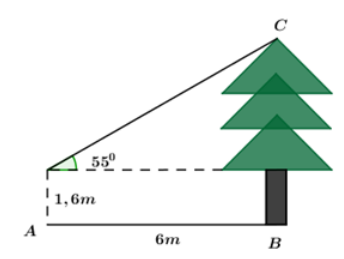
-
A.
\(5,80m\)
-
B.
\(8,57m\)
-
C.
\(6,51m\)
-
D.
\(10,17m\)
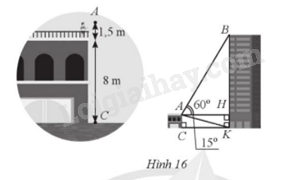
Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là \(\widehat {BAH} = 60^\circ \). Bạn Đức cũng nhìn thấy vị trí K tại chân tòa nhà đó với góc tạo bởi tia AK và tia AH là \(\widehat {HAK} = 15^\circ \), AH vuông góc với BK tại H (Hình 16). Tính chiều cao BK của tòa nhà (làm tròn kết quả đến hàng phần mười của mét).
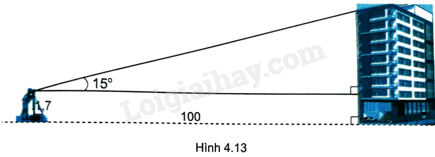
Một người đứng xa tòa nhà 100m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn \({15^o}\) (so với phương nằm ngang) (H.4.13). Hỏi tòa nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7m?
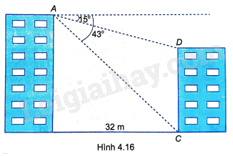
Cho hai tòa nhà cách nhau 32m. Tại điểm A trên nóc tòa nhà cao nhìn xuống nóc D và chân C của tòa nhà thấp lần lượt theo các góc \({15^o}\) và \({43^o}\) (so với phương nằm ngang) (H.4.16). Tính chiều cao của hai tòa nhà đó (làm tròn đến m).
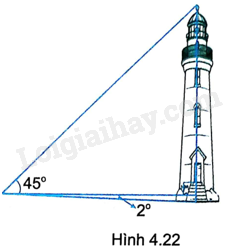
Một người đứng cách chân ngọn hải đăng 50m, nhìn xuống chân hải đăng dưới góc \({2^o}\) và nhìn lên đỉnh ngọn hải đăng dưới góc \({45^o}\) (so với phương nằm ngang) (H.4.22). Tính chiều cao ngọn hải đăng (làm tròn đến mét).
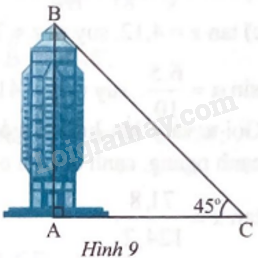
Một du khách đếm được 645 bước chân khi đi từ ngay dưới chân toàn tháp thẳng ra phía ngoài cho đến vị trí có góc nhìn lên đỉnh là 45o (Hình 9). Tính chiều cao của tháp, biết rằng khoảng cách trung bình của mỗi bước chân là 0,4 m.
Tính chiều cao của cột cờ (làm tròn kết quả đến hàng phần trăm của mét), biết bóng của cột cờ được chiếu bởi ánh sáng Mặt Trời xuống mặt đất dài 10,5 m và góc tạo bởi tia sáng với phương nằm ngang là 36°.
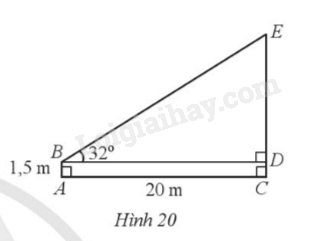
Một người đứng chào cờ (ở vị trí A) cách cột cờ (ở vị trí C) với AC = 20 m. Người đó đặt mắt tại vị trí B cách mặt đất một khoảng là AB = 1,5 m.
Người đó nhìn lên đỉnh cột cờ (ở vị trí E) theo phương BE tạo với phương nằm ngang BD một góc là \(\widehat {EBD} = 32^\circ \) (Hình 20). Tính chiều cao của cột cờ (làm tròn kết quả đến hàng đơn vị của mét).
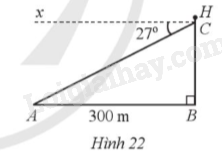
Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat {ACx} = 27^\circ \) (minh hoạ ở Hình 22). Tính chiều cao BH của tháp hải đăng (làm tròn kết quả đến hàng phần trăm của mét), biết AB//Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là CH = 2,1 m.







Danh sách bình luận