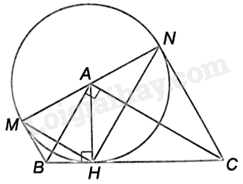
Cho tam giác ABC vuông tại A, có đường cao AH.
a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH;
b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A);
c) Chứng minh rằng MN là một đường kính của (A);
d) Tính diện tích của tứ giác BMNC, biết \(HB = 2cm\) và \(HC = 4,5cm\).
a) + Chỉ ra \(AH \bot BC\) tại H, H thuộc (A, AH) nên BC tiếp xúc với đường tròn (A) bán kính AH.
b) + Chứng minh \(\Delta AMB = \Delta AHB\left( {c.c.c} \right)\).
Do đó, \(\widehat {AMB} = \widehat {AHB} = {90^o}\).
+ Chứng minh M thuộc đường tròn (A). Suy ra, BM vuông góc với AM tại M nên BM là tiếp tuyến của (A) tại M.
+ Chứng minh \(\Delta ANC = \Delta AHC\left( {c.c.c} \right)\).
Do đó, \(\widehat {ANC} = \widehat {AHC} = {90^o}\).
+ Chỉ ra N thuộc đường tròn (A).
+ Suy ra, CN vuông góc với AN tại N nên AN là tiếp tuyến của (A) tại N.
c) + Chứng minh \(\widehat {MAB} = \widehat {HAB}\), \(\widehat {NAC} = \widehat {HAC}\), \(\widehat {HAB} + \widehat {HAC} = {90^o}\).
+ Do đó, \(\widehat {MAB} + \widehat {HAB} + \widehat {NAC} + \widehat {HAC} = {180^o}\)
+ Suy ra, ba điểm M, A, N thẳng hàng. Vậy MN là đường kính của (A).
d) + Chứng minh \(BM = BH\), \(CN = CH\).
+ Do đó, \(BM + CN = BH + CH = 2 + 4,5 = 6,5\left( {cm} \right)\)
+ Chứng minh $\Delta HBA\backsim \Delta HAC\left( g.g \right)$ nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\), từ đó tính được AH, tính được MN.
+ Chứng minh tứ giác BMNC là hình thang vuông.
+ Diện tích hình thang BMNC là: \(S = \frac{1}{2}MN\left( {BM + CN} \right)\).
a) Vì AH là đường cao của tam giác ABC nên \(AH \bot BC\) tại H. Mà H thuộc (A, AH) nên BC tiếp xúc với đường tròn (A) bán kính AH.
b) Vì M đối xứng với H qua AB nên \(AM = AH\) và \(BM = BH\), AB chung nên \(\Delta AMB = \Delta AHB\left( {c.c.c} \right)\).
Do đó, \(\widehat {AMB} = \widehat {AHB} = {90^o}\).
Lại có \(AM = AH\) nên M thuộc đường tròn (A).
Suy ra, BM vuông góc với AM tại M nên BM là tiếp tuyến của (A) tại M.
Vì N đối xứng với H qua AC nên \(CN = CH\) và \(AH = AN\), AC chung nên \(\Delta ANC = \Delta AHC\left( {c.c.c} \right)\).
Do đó, \(\widehat {ANC} = \widehat {AHC} = {90^o}\).
Lại có \(AH = AN\) nên N thuộc đường tròn (A).
Suy ra, CN vuông góc với AN tại N nên AN là tiếp tuyến của (A) tại N.
c) Vì \(\Delta AMB = \Delta AHB\left( {cmt} \right)\) nên \(\widehat {MAB} = \widehat {HAB}\).
Vì \(\Delta ANC = \Delta AHC\left( {cmt} \right)\) nên \(\widehat {NAC} = \widehat {HAC}\).
Vì \(AH \bot BC\) tại H nên \(\widehat {HAB} + \widehat {HAC} = {90^o}\).
Do đó, \(\widehat {MAB} + \widehat {HAB} + \widehat {NAC} + \widehat {HAC} \) \(= 2\left( {\widehat {HAB} + \widehat {HAC}} \right) \) \(= {2.90^o} = {180^o}\)
Suy ra, ba điểm M, A, N thẳng hàng.
Mà \(AM = AN\left( { = AH} \right)\) nên MN là đường kính của (A).
d) Vì MB và BH là hai tiếp tuyến cắt nhau tại B của (A) nên \(BM = BH\).
Vì CN và CH là hai tiếp tuyến cắt nhau tại C của (A) nên \(CN = CH\).
Do đó, \(BM + CN = BH + CH = 2 + 4,5 = 6,5\left( {cm} \right)\).
Ta có:
\(\widehat {BAH} + \widehat {ABC} = \widehat {ACH} + \widehat {ABC}\\\left( { = {{90}^o}} \right)\) nên \(\widehat {BAH} = \widehat {ACH}\).
Mà \(\widehat {BHA} = \widehat {CHA} = {90^o}\) nên $\Delta HBA\backsim \Delta HAC\left( g.g \right)$
nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\),
suy ra \(A{H^2} = BH.CH = 4,5.2 = 9\).
Suy ra \(AH = 3cm\).
Do đó, \(MN = 2AH = 6cm\).
Ta có: \(BM \bot MN,CN \bot MN\) nên BM//NC.
Do đó, tứ giác BMNC là hình thang vuông.
Diện tích hình thang BMNC là:
\(S = \frac{1}{2}MN\left( {BM + CN} \right) = \frac{1}{2}.6.6,5 = 19,5\left( {c{m^2}} \right)\).

Các bài tập cùng chuyên đề
Cho đường tròn \(\left( {O;R} \right)\), lấy điểm \(M\) nằm ngoài \(\left( O \right)\) sao cho \(OM = 2R.\) Từ M kẻ tiếp tuyến \(MA\) và \(MB\) với \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
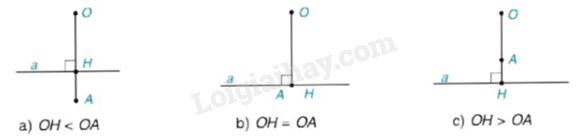
Cho đường thẳng a và điểm O. Gọi H là chân đường vuông góc hạ từ O xuống a, và A là một điểm thuộc tia OH. Trong mỗi trường hợp sau đây, hãy vẽ đường tròn (O; OA) và cho biết đường thẳng a và đường tròn (O; OA) có bao nhiêu điểm chung?
Cho đường thẳng a và điểm O cách a một khoảng bằng 4 cm. Không vẽ hình, hãy dự đoán xem mỗi đường tròn sau cắt, tiếp xúc hay không cắt đường thẳng a. Tại sao?
a) (O; 3 cm)
b) (O; 5 cm)
c) (O; 4 cm)
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình tròn nào sẽ che khuất một phần của đường thẳng a, hình tròn nào sẽ không che khuất một phần của đường thẳng a?
Cho hai đường thẳng a và b song song với nhau, điểm O nằm trong phần mặt phẳng ở giữa hai đường thẳng đó. Biết rằng khoảng cách từ O đến a và b lần lượt bằng 2 cm và 3 cm.
a) Hỏi bán kính của đường tròn (O; R) phải thỏa mãn điều kiện gì để (O; R) cắt cả hai đường thẳng a và b?
b) Biết rằng đường tròn (O; R) tiếp xúc với đường thẳng a. Hãy xác định vị trí tương đối của đường tròn (O; R) và đường thẳng b.
Cho đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó \({\rm{B}} \in \left( {\rm{O}} \right)\) và \({\rm{C}} \in \left( {{\rm{O'}}} \right)\). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng:
a) Đường thẳng MA tiếp xúc với (O’);
b) Điểm M là trung điểm của đoạn thẳng BC, từ đó suy ra ABC là tam giác vuông.
Cho đường tròn (O; R) và hai đường thẳng \({{\rm{a}}_1}\)và \({{\rm{a}}_2}.\) Gọi \({{\rm{d}}_1},{{\rm{d}}_2}\) lần lượt là khoảng cách từ điểm O đến \({{\rm{a}}_1}\)và \({{\rm{a}}_2}.\) Biết rằng (O) cắt \({{\rm{a}}_1}\) và tiếp xúc với \({{\rm{a}}_2}\) (H.5.45).
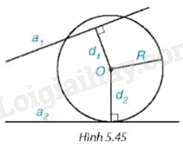
Khi đó:
A. \({{\rm{d}}_1} < {\rm{R}}\)và \({{\rm{d}}_2} = {\rm{R}}\)
B. \({{\rm{d}}_1} = {\rm{R}}\)và \({{\rm{d}}_2} < {\rm{R}}\)
C. \({{\rm{d}}_1} > {\rm{R}}\)và \({{\rm{d}}_2} = {\rm{R}}\)
D. \({{\rm{d}}_1} < {\rm{R}}\)và \({{\rm{d}}_2} < {\rm{R}}\)
Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau:
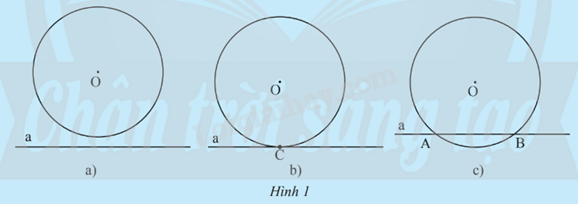
Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:
a) d = 4 cm
b) d = 5 cm
c) d = 6 cm
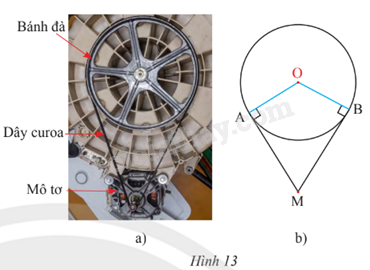
Bánh đà của một động cơ được thiết kế có dạng một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.
a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).
b) Tính số đo \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM và số đo \(\widehat {AOB}\) (kết quả làm tròn đến phút).
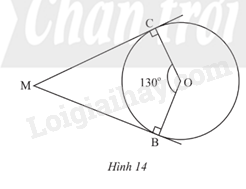
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\) .
Cho đường tròn (O; 5 cm) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) vuông góc với nhau tại M.
a) Tính độ dài MA và MB.
b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài CD.
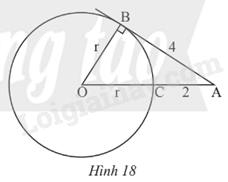
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.
a) Tính bán kính r của đường tròn (O).
b) Tính chiều dài cạnh OA của tam giác ABO.
Cho đường tròn (O; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4 cm. Kết luận nào sau đây đúng về vị trí giữa đường tròn (O) và đường thẳng a?
A. (O) và a cắt nhau tại hai điểm.
B. (O) và a tiếp xúc.
C. (O) và a không có điểm chung.
D. (O) và a có duy nhất điểm chung.
Cho điểm \(O\) và đường thẳng \(a\) thỏa mãn khoảng cách từ \(O\) đến đường thẳng \(a\) bằng 4cm. Xác định vị trí tương đối của đường thẳng \(a\) và các đường tròn \(\left( {O;3cm} \right),\left( {O;4cm} \right),\left( {O;5cm} \right)\).
Đồng hồ treo tường trang trí ở Hình 29 gợi nên vị trí tương đối của đường thẳng và đường tròn. Quan sát Hình 29 và chỉ ra hình ảnh đường thẳng và đường tròn:
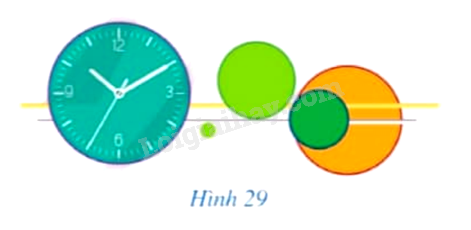
a) Cắt nhau;
b) Tiếp xúc nhau;
c) Không giao nhau.
Cho bốn điểm \(O,M,N,P\) cùng nằm trên một đường thẳng sao cho điểm \(M\) nằm giữa hai điểm \(O\) và \(N\); điểm \(N\) nằm giữa hai điểm \(M\) và \(P\). Gọi \(a,b,c\) lần lượt là các đường thẳng đi qua \(M,N,P\) và vuông góc với đường thẳng \(OP\). Xác định vị trí tương đối của mỗi đường thẳng \(a,b,c\) và đường tròn \(\left( {O;ON} \right)\).
Cho điểm \(O\) và đường thẳng \(a\) không đi qua \(O\).
a) Vẽ điểm \(H\) là hình chiếu của điểm \(O\) trên đường thẳng \(a\).
b) Từ đó, vẽ ba đường tròn tâm \(O\) lần lượt: không giao với đường thẳng \(a;\) tiếp xúc với đường thẳng \(a;\) cắt đường thẳng \(a\) tại hai điểm phân biệt.
Cho hình vuông \(ABCD\) cạnh \(r\) và đường tròn \(\left( {C;r} \right)\) giả sử \(M\) là một điểm nằm trên đường tròn \(\left( {C;r} \right)\) sao cho điểm \(M\) nằm trong hình vuông \(ABCD\). Tiếp tuyến của đường tròn \(\left( {C;r} \right)\) tại tiếp điểm \(M\) cắt các đoạn thẳng \(AB,AD\) lần lượt tại \(N,P\). Chứng minh:
a) Các đường thẳng \(NB,PD\) là các tiếp tuyến của đường tròn \(\left( {C;r} \right)\).
b) \(\widehat {NCP} = \widehat {NCB} + \widehat {PCD} = 45^\circ \).
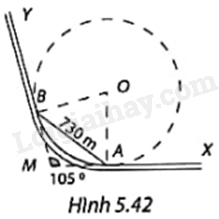
Trong trường hợp nào ở Hình 5.29, đoàn tàu có thể di chuyển từ cung đường ray AB sang đường ray thẳng BC mà không trật bánh ray? Khi đó đường thẳng BC và đường tròn (O) có vị trí tương đối như thế nào?
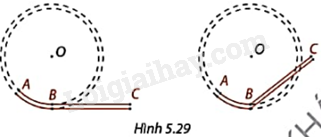
Trong Hình 5.30, đường thẳng a tiếp xúc với đường tròn (O; R) tại A và H là chân đường vuông góc kẻ từ O xuống a. Xác định độ dài OH. Vì sao A và H trùng nhau, nhận xét về góc tạo bởi tiếp tuyến a và bán kính OA.
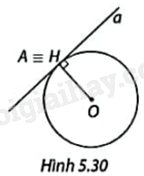
Hình 5.41 cho thấy mặt cắt của hai ống nước nhựa được đặt sát nhau trên mặt đất. Ống nhỏ có đường kính 6cm, ống lớn có đường kính 18cm. Tính:
a) Khoảng cách AB giữa tâm của hai mặt cắt;
b) Khoảng cách HK giữa hai tiếp điểm của mặt cắt hai ống với mặt đất.
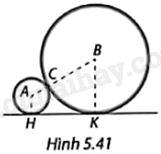
Trong Hình 5.42, để tàu không trật bánh ray khi chuyển hướng từ đường ray thẳng XA sang đường ray thẳng YB, đoạn ray nối được thiết kế là một phần của đường tròn (O) tiếp xúc với XA tại A và BY tại B. Biết góc chuyển hướng của tàu là \(\widehat {AMB} = {105^o}\) và khoảng cách giữa hai điểm A và B là 730m. Tính bán kính của đường tròn (O). Làm tròn kết quả đến đơn vị mét.
Vị trí của mặt trời so với đường chân trời có gì khác biệt trong các Hình 5.24a, b và c?

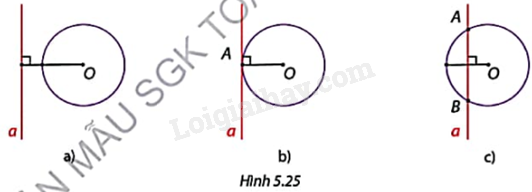
Hình 5.25 thể hiện vị trí tương đối khác nhau của đường thẳng a và đường tròn (O) khi đường thẳng a di chuyển từ ngoài về gần tâm O của đường tròn. Nêu số điểm chung của đường thẳng a và đường tròn (O) trong mỗi trường hợp.
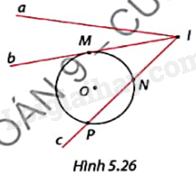
Xác định vị trí tương đối của đường tròn (O) với các đường thẳng a, b và c trong Hình 5.26. Chỉ ra tiếp điểm, giao điểm của chúng (nếu có).
Xác định vị trí tương đối của đường thẳng a đến đường tròn (O; 7cm) nếu khoảng cách từ O đến a bằng:
a) 4cm;
b) 9cm;
c) 7cm.
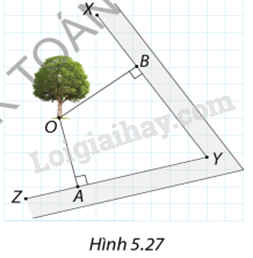
Trong Hình 5.27, mỗi ô vuông tương ứng với độ dài 1m. Có thể quây một hàng rào tròn bán kính 5m với tâm tại vị trí cây xanh O mà không cắt vào đường bao XY và YZ không?
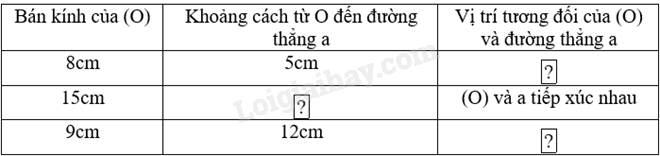
Thay các ô ? trong bảng dưới đây bằng một độ dài hoặc một khẳng định thích hợp.
Trên mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Xác định:
a) Vị trí tương đối của đường tròn tâm M, bán kính 3 với hai trục Ox và Oy;
b) Bán kính của đường tròn tâm M tiếp xúc với trục Ox.







Danh sách bình luận