Giải tam giác ABC vuông tại A, với \(AB = c,BC = a,CA = b\) trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba):
a) \(a = 5,\widehat B = {50^o}\);
b) \(b = 5,\widehat B = {40^o}\);
c) \(b = 5,\widehat C = {55^o}\).
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
a) Ta có: \(\widehat C = {90^o} - \widehat B = {40^o}\),
\(c = 5.\cos B \approx 3,214;\\b = 5\sin B = 5.\sin {50^o} \approx 3,830\)
b) Ta có: \(\widehat C = {90^o} - \widehat B = {50^o}\),
\(b = asinB\) nên \(a = \frac{b}{{\sin B}} = \frac{5}{{\sin {{40}^o}}} \approx 7,779\),
\(b = c.\tan B\) nên \(c = \frac{b}{{\tan B}} = \frac{5}{{\tan {{40}^o}}} \approx 5,959\).
c) \(\widehat B = {90^o} - \widehat C = {35^o}\),
\(b = a.\cos C\) nên \(a = \frac{b}{{\cos C}} = \frac{5}{{\cos {{55}^o}}} \approx 8,717\),
\(c = b.\tan C = 5.\tan {55^o} \approx 7,141\).
Các bài tập cùng chuyên đề
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,AB = 12\,cm\) . Tính $AC;\widehat B$ .
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến số thập phân thứ ba) và các góc B, C (làm tròn đến độ).
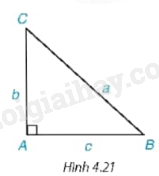
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh \(AB = c,AC = b\) hoặc \(AB = c,BC = a\) và không sử dụng định lý Pythagore (H.4.21).
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Giải tam giác ABC vuông tại A, biết \(BC = 9,\widehat C = {53^0}.\)
Giải bài toán ở tình huống mở đầu với \(\alpha = {27^0},\beta = {19^0}.\)
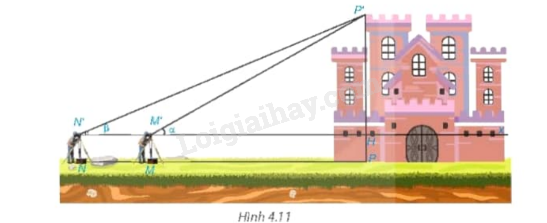
Tình huống mở đầu: Để đo chiều cao của một tòa lâu đài (H.4.11) , người ta đặt giác kế thẳng đứng tại M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của tòa lâu đài dưới góc nhọn \(\alpha \). Sau đó, đặt giác kế thẳng đứng tại N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn \(\beta \left( {\beta < \alpha } \right).\) Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của tòa lâu đài.
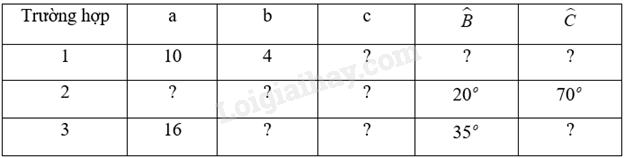
Giải tam giác ABC vuông tại A có \(BC = a,AC = b,AB = c,\) trong các trường hợp (góc làm tròn đến độ, độ dài cạnh làm tròn đến chữ số hàng đơn vị):
a) \(a = 21,b = 18;\)
b) \(b = 10,\widehat C = {30^0};\)
c) \(c = 5,b = 3.\)
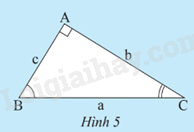
Cho tam giác ABC (Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và các góc của tam giác. Giải thích cách tính.
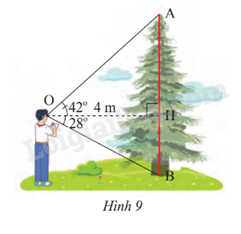
Trong Hình 9, cho OH = 4 m, \(\widehat {AOH} = {42^o},\widehat {HOB} = {28^o}\). Tính chiều cao AB của cây.
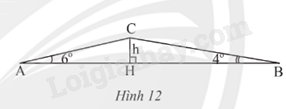
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762m, \(\widehat A = {6^o},\widehat B = {4^o}\).
a) Tính chiều cao h của con dốc
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.
Cho tam giác OPQ vuông tại O có \(\widehat P = {39^o}\) và PQ = 10 cm. Hãy giải tam giác vuông OPQ.
Tìm độ dài cạnh góc vuông \(AC\) và số đo các góc nhọn \(B,C\) của tam giác vuông \(ABC\), biết cạnh góc vuông \(AB = 5cm\) và cạnh huyền \(BC = 13cm\).
Tìm số đo góc nhọn \(C\) và độ dài cạnh góc vuông \(AB\), cạnh huyền \(BC\) của tam giác vuông \(ABC\), biết cạnh góc vuông \(AC = 7cm\) và \(\widehat B = 55^\circ \).
Cho hình chữ nhật \(ABCD\) thỏa mãn \(AC = 6cm,\widehat {BAC} = 47^\circ \). Tính độ dài các đoạn thẳng \(AB,AD\).
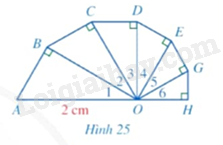
Tính độ dài đường gấp khúc \(ABCDEGH\), biết các tam giác \(OAB,OBC,OCD,ODE,OEG,OGH\) là các tam giác vuông tại các đỉnh lần lượt là \(B,C,D,E,G,H\); các góc \({O_1},{O_2},{O_3},{O_4},{O_5},{O_6}\) đều bằng \(30^\circ \) và \(OA = 2cm\) (Hình 25).
Hình 26 minh hoạ một phần con sông có bề rộng \(AB = 100m\).Một chiếc thuyền đi thẳng từ vị trí \(B\) bên này bờ sông đến vị trí \(C\) bên kia bờ sông. Tính quãng đường \(BC\) (làm tròn kết quả đến hàng phần mười của mét), biết \(\widehat {ABC} = 35^\circ \).
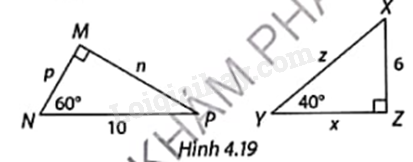
Tính các độ dài n, p, x, z trong Hình 4.19. Làm tròn kết quả đến hàng phần trăm.
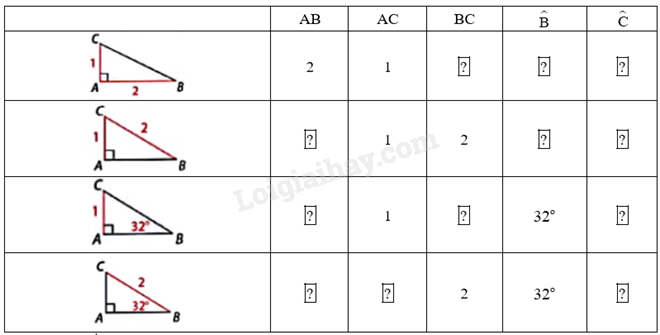
Trong mỗi trường hợp dưới đây, hãy xác định độ dài các cạnh và số đo góc ở các ô . Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười. Cho biết em đã sử dụng hệ thức, định lí nào để tính.
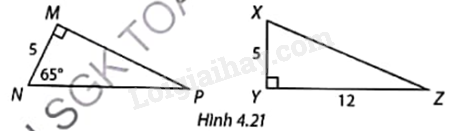
Giải các tam giác vuông MNP và XYZ trong Hình 4.21. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười.
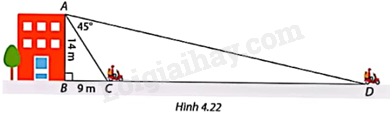
Trong Hình 4.22, một người đứng từ sân thượng tòa nhà và quan sát một người đi xe máy từ vị trí C đến vị trí D.
a) Giải tam giác vuông ABD.
b) Tính tốc độ của xe máy, biết thời gian xe đi từ C đến D là 6,5 giây. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười mét.
Giải tam giác ABC vuông tại A, biết:
a) \(AC = 11cm,\widehat C = {60^o}\);
b) \(BC = 20cm,\widehat C = {35^o}\);
c) \(AB = 7cm,AC = 12cm\);
d) \(AB = 9cm,BC = 20cm\).
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
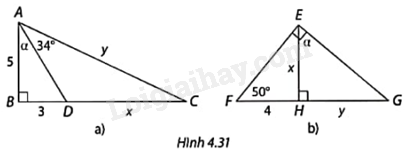
Tính số đo góc \(\alpha \) và các độ dài x, y trong mỗi trường hợp ở Hình 4.31.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7\,cm,AB = \,5cm\). Tính $BC;\widehat C$ .
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 26\,cm,AB = 10\,cm\) Tính \(AC;\widehat B\) . (làm tròn đến độ)
Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\) đường cao \(CH = 3,6\). Hãy giải tam giác \(ABC\).
Cho tam giác vuông có cạnh huyền bằng 25 cm, một góc nhọn bằng 29o. Tính các cạnh còn lại của tam giác đó.
Độ dài cạnh BC trong Hình 2 (kết quả làm tròn đến hàng phần trăm) là
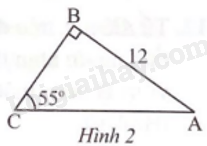
A. 17,14
B. 9,83
C. 8,40
D. 6,88
Khoảng cách giữa hai chân tháp AB và MN là x (Hình 3). So với phương nằm ngang AH, từ đỉnh A của tháp AB nhìn lên đỉnh M của tháp MN ta được góc \(\alpha \), từ đỉnh A của tháp AB nhìn xuống chân N của tháp MN ta được góc \(\beta \). Cho biết x = 120 m, \(\alpha \) = 30o và \(\beta \) = 20o . Chiều cao của tháp MN (kết quả làm tròn đến hàng đơn vị của mét) là
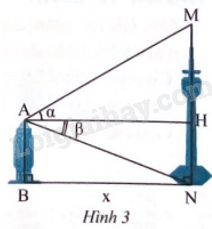
A. 113 m
B. 25 m
C. 101 m
D. 21,7 m
Cho tam giác ABC vuông tại A có đường cao AH, BH = 1 cm, CH = 4 cm. Giải tam giác ABC.
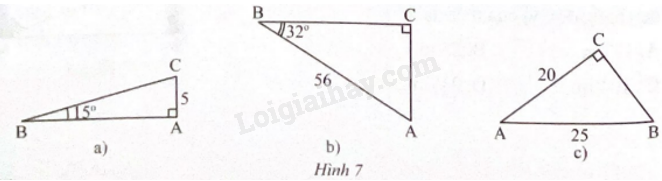
Giải các tam giác vuông trong Hình 7.
Cho tam giác ABC có AB = 15 cm, BC = 20 cm, \(\widehat {ABC} = {64^o}\). Tính độ dài:
a) đường cao AH;
b) các đoạn thẳng BH, CH;
c) cạnh AC
