Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho \(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}}\). Giao tuyến của hai mặt phẳng (DBC) và (DMN) là:
A. Đường thẳng qua D song song với MN
B. Đường thẳng qua D song song với BC
C. Cả A, B đều đúng
D. Cả A, B đều sai
Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
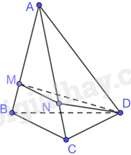
Tam giác ABC có: \(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}}\) nên MN//BC.
Vì mặt phẳng (DMN) đi qua đường thẳng MN, mặt phẳng (DBC) đi qua đường thẳng BC và D là điểm chung của hai mặt phẳng (DBC) và mặt phẳng (DMN).
Do đó, giao tuyến của hai mặt phẳng (DBC) và (DMN) là đường thẳng qua D song song với MN và BC.
Đáp án C







