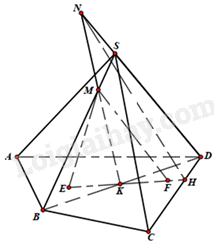
Cho hình chóp tứ giác S. ABCD, M là một điểm trên cạnh SB. Gọi E, F là hai điểm lần lượt thuộc miền trong tam giác ABD và tam giác BCD. Giao tuyến của mặt phẳng (MEF) và mặt phẳng (SCD) là:
A. HN, với N là giao điểm của ME và SD, H là giao điểm của EF và CD
B. HN, với K là giao điểm của EF và BD, N là giao điểm của MK và SD, H là giao điểm của EF và CD
C. HN, với N là giao điểm của MF và SD, H là giao điểm của EF và CD
D. HN, với K là giao điểm của EF và BD, N là giao điểm của MK và SC, H là giao điểm của EF và CD
Nếu hai mặt phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).
|
Trong mặt phẳng (ABCD), gọi K là giao điểm của EF và BD, H là giao điểm của của EF và CD nên \(H \in \left( {MEF} \right) \cap \left( {SCD} \right)\) Trong mặt phẳng (SBD), gọi N là giao điểm của MK và SD nên \(N \in \left( {MEF} \right) \cap \left( {SCD} \right)\) Vậy HN là giao tuyến mặt phẳng (MEF) và mặt phẳng (SCD). Đáp án B |
 |
