Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = 4{\cos ^2}x - 4\cos x + 3\) với \(x \in \left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\).
Phương pháp giải
B1: Đặt ẩn phụ và tìm điều kiện của ẩn
B2: Lập bảng biến thiên, khảo sát hàm số rồi kết luận
Lời giải của GV Loigiaihay.com
Đặt \(t = \cos x\).
Với \(\frac{\pi }{3} \le x \le \frac{{5\pi }}{6}\) ta có \(\frac{{ - \sqrt 3 }}{2} \le t \le \frac{1}{2}\) .
Khi đó ta có \(y = f\left( t \right) = 4{t^2} - 4t + 3\) , \(\frac{{ - \sqrt 3 }}{2} \le t \le \frac{1}{2}\).
Ta có bảng biến thiên:
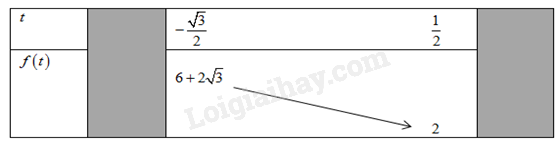
Từ bảng biến thiên ta có:
Giá trị lớn nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\) là \(6 + 2\sqrt 3 \).
Giá trị nhỏ nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\) là \(2\).
