1. Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có độ dài cạnh đáy là 14cm; chiều cao của giá đèn cầy là 22cm. Mặt bên của giá đèn cầy là các tam giác cân có chiều cao là 23cm. Tính diện tích xung quanh và thể tích của giá đèn cầy có dạng hình chóp tứ giác đều với kích thước như trên.
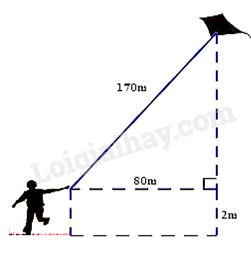
2. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2m.
1. Sử dụng công thức tính diện tích xung quanh và thể tích của hình chóp tứ giác đều.
2. Sử dụng định lí Pythagore.
1. Diện tích xung quanh của giá đèn cầy hình chóp tứ giác đều :
\({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.(4.14).23 = 644(c{m^2})\)
Thể tích của giá đèn cầy hình chóp tứ giác đều :
\(V = \frac{1}{3}.S.h = \frac{1}{3}.(14.14).22 = \frac{{4312}}{3}(c{m^3})\)
2.
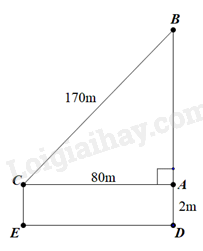
Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A:
\(B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow AB = \sqrt {{{170}^2} - {{80}^2}} = 150\)
+ Độ cao của con diều so với mặt đất 150 + 2 = 152m
