Cho hình chóp S.ABCD đều có thể tích bằng 200cm³ , chiều cao SO bằng 12cm. Độ dài cạnh bên của hình chóp tứ giác đó là :

A. 12cm.

B. 13cm.

C. 11cm.

D. 16cm.

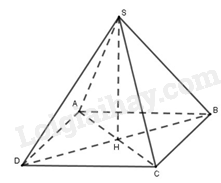
Ta có: \(V = \frac{1}{3}SO.{S_{ABCD}}\)

\(\begin{array}{l} \Leftrightarrow 200 = \frac{1}{3}.12.{S_{ABCD}}\\ \Rightarrow {S_{ABCD}} = \frac{{200}}{{\frac{1}{3}.12}} = \frac{{200}}{4} = 50\\ \Leftrightarrow B{C^2} = 50\end{array}\)

Tam giác BHC vuông cân nên HB² + HC² = BC² hay 2HC² = BC² hay 2HC² = 50

Suy ra HC² = 25

SC² = SH² + HC² = 12² + 25² = 169 = 13².

Vậy độ dài cạnh bên là 13cm.

Đáp án B.