Cho tam giác \(ABC\) vuông cân tại \(A,\) đường cao \(AH.\) Gọi \(M\) là trung điểm của \(AB,{\rm{ }}E\) đối xứng với \(H\) qua \(M.\)

1.  Tứ giác \(AHBE\) là hình gì? Vì sao?

2.  Chứng minh \(AEHC\) là hình bình hành.

3.  Gọi \(O\) là giao điểm của \(AH\)và \(EC,{\rm{ }}N\) là trung điểm của \(AC.\) Chứng minh \(M,O,N\) thẳng hàng.

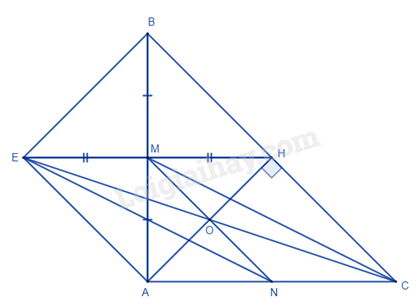
1. Xét tam giác ABC vuông cân tại A, ta có AH là đường cao nên AH cũng là đường trung tuyến ứng với cạnh huyền của tam giác ABC => AH = \(\frac{1}{2}\)BC = BH = HC.

Xét tứ giác AHBE có:

AM = MB (M là trung điểm của AB).

EM = MH (E đối xứng với H qua M).

=> AHBE là hình bình hành (hai đường chéo cắt nhau tại trung điểm).

Xét hình bình hành AHBE có \(\widehat {AHB} = {90^0}\) => AHBE là hình chữ nhật (hình bình hành có một góc vuông).

Xét hình chữ nhật AHBE có AH = BH (cmt) => AHBE là hình vuông (hình chữ nhật có hai cạnh kề bằng nhau).

=> AE // BH, AE = BH.

2. Xét tứ giác AEHC có:

AE // HC (vì AE // BH)

AE = HC (= HB)

=> AEHC là hình bình hành (cặp cạnh đối song song và bằng nhau). (đpcm)

3. Vì O là giao điểm của AH và EC nên O là trung điểm của EC => EO = OC.

Vì AEHC là hình bình hành nên EH // AC và EH = AC.

Ta có M là trung điểm của EH, N là trung điểm của AC nên EM = MH = \(\frac{1}{2}\)EB = \(\frac{1}{2}\)AC = AN = NC.

Xét tứ giác EMCN có:

EM // CN (vì EH // AC)

EM = CN (cmt)

=> EMCN là hình bình hành (cặp cạnh đối song song và bằng nhau)

=> EC cắt MN tại trung điểm của mỗi đường. Mà O là trung điểm của EC nên O cũng là trung điểm của MN, hay M, O, N thẳng hàng (đpcm).