Cho \(\angle xOy = {30^0}\), vẽ góc \(\angle xOt = {70^0}\) sao cho tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot\).

a) Tính \(\angle yOt?\) Tia \(Oy\) có là tia phân giác của góc \(\angle xOy\) không? Vì sao?

b) Gọi tia \(Om\) là tia đối của tia \(Ox\). Tính số đo của \(\angle mOt?\)

c) Gọi \(Oz\) là tia phân giác của \(\angle mOt\). Tính số đo của \(\angle yOz?\) 

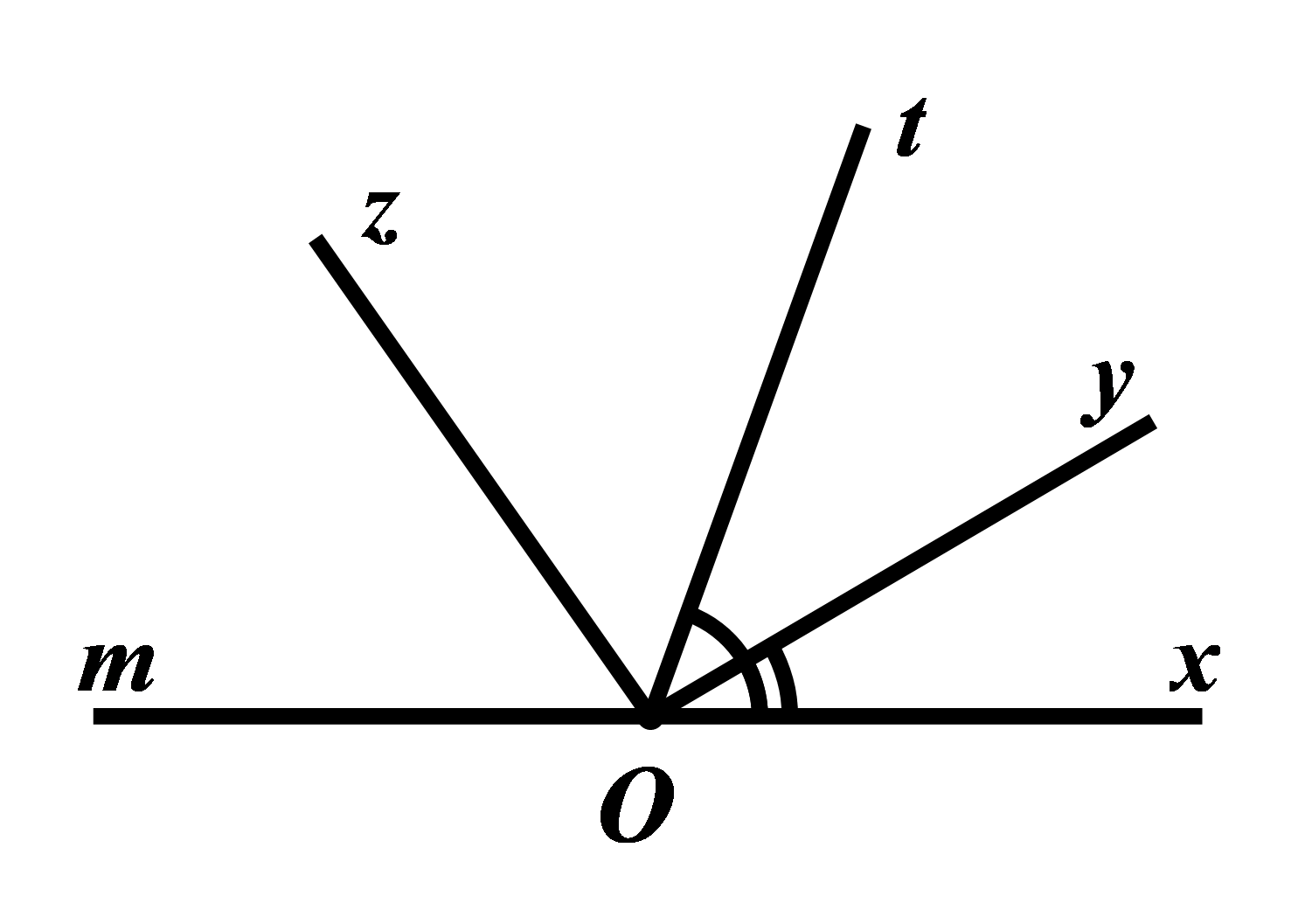
a) * Vì \(\angle xOy\) và \(\angle yOt\) là hai góc kề nhau nên ta có: \(\angle xOy + \angle yOt = \angle xOy\)

\(\begin{array}{l} \Rightarrow {30^0} + \angle yOt = {70^0}\\ \Rightarrow \angle yOt = {70^0} - {30^0}\\ \Rightarrow \angle yOt = {40^0}\end{array}\)

Vậy \(\angle yOt = {40^0}\).

* Vì \(\angle xOy = {30^0};\angle yOt = {40^0}\) nên hai góc \(\angle xOy\) và \(\angle yOt\) không bằng nhau

Do đó, \(Oy\) không là tia phân giác của \(\angle xOt\).

b) Vì \(Om\) là tia đối của tia \(Ox\) nên \(\angle xOm\) là góc bẹt và bằng \({180^0}\).

Ta có: \(\angle xOt\) và \(\angle tOm\) là hai góc kề bù nên \(\angle xOt + \angle tOm = {180^0}\)

\(\begin{array}{l} \Rightarrow {70^0} + \angle tOm = {180^0}\\ \Rightarrow \angle tOm = {180^0} = {70^0}\\ \Rightarrow \angle tOm = {110^0}\end{array}\)

Vậy \(\angle tOm = {110^0}\)

c) Vì \(Oz\) là tia phân giác của \(\angle mOt\) (giả thiết) nên \(\angle zOt = \dfrac{1}{2}\angle mOt = \dfrac{1}{2}{.110^0} = {55^0}\)

Hai góc \(\angle yOt\) và \(\angle tOz\) kề nhau nên \(\angle yOt + \angle tOz = \angle yOz\)

\(\begin{array}{l} \Rightarrow {40^0} + {55^0} = \angle yOz\\ \Rightarrow {95^0} = \angle yOz\end{array}\)

Vậy \(\angle yOz = {95^0}\)