Một đội xe chuyển \(945\) tấn hàng từ kho tổng về cửa hàng.
Biết mỗi ngày đội xe đó chuyển được \(35\) tấn. Gọi \(y\) (tấn) là khối lượng hàng hóa trong kho tổng sau \(x\) ngày vận chuyển.
a) Viết công thức tính \(y\) theo \(x\). Hỏi \(y\) có phải hàm số bậc nhất của \(x\) hay không?
b) Đội xe đó cần bao nhiêu ngày để chuyển hết 945 tấn hàng từ kho tổng về cửa hàng?
a) Viết công thức tính \(y\) theo \(x\). Dựa vào định nghĩa hàm số để trả lời câu hỏi.
b) Để chuyển hết \(945\) tấn hàng thì số hàng còn lại trong kho hàng bằng 0. Tính giá trị của \(x\) khi \(y = 0.\)
a) \(y = 945 - 35x\). Vậy \(y\) là hàm số của \(x\) vì với mỗi giá trị của \(x\) chỉ xác định đúng một giá trị của \(y.\)
b) Để chuyển hết \(945\) tấn hàng thì số hàng còn lại trong kho hàng bằng 0 hay \(y = 0\). Ta được \(0 = 945 - 35x\) suy ra \(x = 27.\)
Vậy đội xe đó cần 27 ngày để chuyển hết 945 tấn hàng từ kho tổng về cửa hàng.
Các bài tập cùng chuyên đề
Cho biết đại lượng \(y\) được tính theo đại lượng \(x\) như sau: \(y = 2x + 3\)
a) Tính \(y\) khi \(x = 4\).
b) Cho \(x\) một giá trị tùy ý, tính giá trị tương ứng của \(y\).
Một doanh nghiệp xuất khẩu gạo thu mua lúa với giá 7 triệu đồng/ tấn. Do thóc thu mua được có chất lượng cao nên doanh nghiệp đã thưởng thêm cho nhà sản xuất 6 triệu đồng. Gọi y (triệu đồng) là tổng số tiền mà doanh nghiệp đã trả cho nhà sản xuất để mua x tấn thóc. Viết công thức tính y theo x.
Hàm số cho bằng công thức tính y theo x ở trên gợi nên khái niệm nào trong toán học.
Trong bài toán mở đầu, y có phải là đa thức bậc nhất của biến x hay không?
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Đối với những hàm số bậc nhất đó, xác định a, b lần lượt là hệ số của x, hệ số tự do.
a) \(y = - 3{\rm{x + 6}}\)
b) \(y = - x + 4\)
c) \(y = \dfrac{3}{x} + 2\)
d) \(y = 2\)
Cho hàm số \(y = - 2{\rm{x}} + 4\). Tìm giá trị của y tương ứng với mỗi giá trị sau của x: x = 0; x = 2; x = 4.
Nếu hiện tại nước Anh là mùa đông thì London ở múi giờ + 0, Hà Nội múi giờ + 7. Giả sử vào thời điểm mùa đông của nước Anh, giờ London là x (giờ), giờ Hà Nội là y (giờ). Viết công thức biểu thị y theo x. Hỏi y có phải là hàm số bậc nhất của x hay không?
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước
b) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và a khác 0.
c) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và b khác 0.
Xác định hệ số của x, hệ số tự do trong mỗi hàm số bậc nhất sau:
\(a) y = 6{\rm{x}} + 8\)
\(b) y = - x - 5\)
\(c) y = \dfrac{x}{3}\)
Cho hàm số bậc nhất \(f(x) = 3{\rm{x}} + 2\). Tính \(f(1);f(0);f( - 2);f\left( {\dfrac{1}{2}} \right);f\left( { - \dfrac{2}{3}} \right)\).
Hiện tại, bạn Nam đã để dành được 300 000 đồng. Bạn Nam đang có ý định mua một chiếc xe đạp trị giá 2 000 000 đồng. Để thực hiện được điều trên, bạn Nam đã lên kế hoạch hằng ngày đều tiết kiệm 5 000 đồng. Gọi m (đồng) là số tiền bạn Nam tiết kiệm được sau 1 ngày.
a) Viết công thức biểu thị m theo t. Hỏi m có phải là hàm số bậc nhất của t hay không?
b) Hỏi sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó?
Một người đang sử dụng internet, mỗi phút tốn dung lượng 1 MB. Giả sử gói cước Internet của người đó cho phép sử dụng dung lượng 4 GB.
a) Viết hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng internet x (giây).
b) Viết hàm số g(x) biểu thị dung lượng còn lại (MB) sau khi sử dụng Internet được x (giây).
c) Sau khi sử dụng Internet 2 phút thì dung lượng cho phép còn lại bao nhiêu Megabyte?
Bạn Dương mang theo 100 000 đồng và đạp xe đạp đi nhà sách để mua vở. Biết giá mỗi quyển vở là 7 000 đồng, phí gửi xe đạp là 3000 đồng.
a) Viết công thức biểu thị tổng số tiền y (đồng) bạn Dương cần phải trả cho việc gửi xe đạp và mua x quyển vở. Hỏi y có phải là hàm số bậc nhất của x hay không?
b) Tính số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở?
c) Viết công thức biểu thị số tiền còn lại t (đồng) bạn Dương còn lại sau khi gửi xe và mua x quyển vở. Hàm số cho bởi công thức đó có phải là hàm số bậc nhất hay không?
d) Với số tiền trên, bạn Dương có thể mua được 15 quyển vở hay không? Vì sao?
Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Chẳng hạn, các khu vực của Thành Phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760 mmHg; Thành phố Puebla (Mexico) có độ cao h = 2 200 m so với mực nước biển nên có áp suất khí quyển là p = 550,4 mmHg. Người ta ước lượng được áp suất khí quyển p (mmHg) tương ứng với độ cao h (m) so với mực nước biển là một hàm số bậc nhất có dạng p = ah + b \((a \ne 0)\).
a) Xác định hàm số bậc nhất đó.
b) Cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển là bao nhiêu mmHG (làm tròn đến hàng phần mười)?
Cho hàm số bậc nhất \(f\left( x \right) = 3x - 1\). Hãy sắp xếp các giá trị sau theo thứ tự giảm dần: \(f\left( { - \frac{1}{3}} \right);f\left( {\frac{1}{9}} \right);f\left( { - 1} \right);f\left( { - 3} \right);f\left( 0 \right).\)
Xác định hệ số của \(x\), hệ số tự do trong mỗi hàm số bậc nhất sau:
a) \(y = 3,6x - 2,7\);
b) \(y = - \sqrt {56} x + 3\);
c) \(y = \frac{{91}}{{112}}x + \frac{{15}}{{67}}\);
d) \(y = - \frac{5}{{29}}x - \sqrt 7 \).
Một cửa hàng thu mua gạo cho biết: Giá nhập vào của \(1\,kg\) gạo tám Hải Hậu là \(18\,000\) đồng.
a) Viết công thức biểu thị số tiền \(y\) (đồng) mà cửa hàng phải trả để nhập \(x\,\left( {kg} \right)\) gạo tám Hải Hậu. Hỏi \(y\) có phải hàm số bậc nhất của \(x\) hay không?
b) Tính số tiền mà cửa hàng phải trả để nhập \(0,5\) tấn gạo tám Hải Hậu.
Nhiệt độ ở mặt đất đo được khoảng \(28^\circ C\). Biết rằng cứ lên cao \(1\,km\) thì nhiệt độ giảm đi \(5^\circ C\).
a) Viết công thức biểu thị nhiệt độ \(y\left( {^\circ C} \right)\) đo được ở độ cao \(x\,\left( {km} \right)\) so với mặt đất. Hỏi \(y\) có phải hàm số bậc nhất của \(x\) hay không?
b) Tính nhiệt độ đo được ở độ cao \(3\,000\,m\) so với mặt đất.
Giá nước sinh hoạt của một hộ gia đình được tính như sau: \(10{m^3}\) đầu tiên giá \(7000\) đồng/\({m^3}\); từ trên \(10{m^3}\) đến \(20{m^3}\) giá \(8200\) đồng/\({m^3}\); từ trên \(20{m^3}\) đến \(30{m^3}\) giá \(10000\) đồng/\({m^3}\); từ trên \(30{m^3}\) giá \(18\,000\) đồng/\({m^3}.\)
a) Viết công thức biểu thị số tiền \(y\) (đồng) mà nhà bạn Mai phải trả khi sử dụng \(x\,\left( {{m^3}} \right)\) trong tháng 12/2020 với \(x > 30.\) Hỏi \(y\) có phải hàm số bậc nhất của \(x\) hay không?
b) Nhà bạn Mai đã phải trả \(342\,000\) đồng cho tiền nước tháng 1/2023. Tính số mét khối nước nhà bạn Mai đã sử dụng trong tháng 1/2023, biết rằng số nước đó lớn hơn \(30{m^3}\).
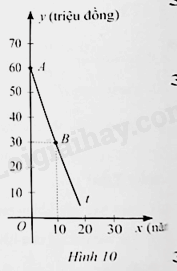
Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao \(k\) (triệu đồng) với \(0 < k < 60\). Gọi \(y\) (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng.
a) Chứng tỏ rẳng \(y\) là hàm số bậc nhất của \(x\), tức là \(y = ax + b\left( {a \ne 0} \right)\).
b) Trong Hình 10, tia \(At\) là một phần của đường thẳng \(y = ax + b\). Tìm \(a,b\). Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.
Hiện tại, cô Hạnh đã tiết kiệm được 500 triệu đồng. Để thực hiện dự định mua một căn chung cư có giá trị 2,6 tỉ đồng, cô Hạnh đã lên kế hoạch hằng tháng tiết kiệm 15 triệu đồng. Gọi \(y\) (triệu đồng) là số tiền cô Hạnh tiết kiệm được sau \(x\) (tháng) kể từ hiện tại.
a) Viết công thức tính \(y\) theo \(x\). Hỏi \(y\) có phải là hàm số bậc nhất của \(x\) hay không?
b) Hỏi sau bao lâu kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm?
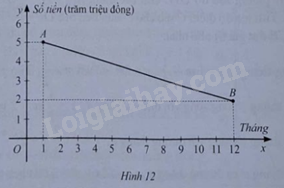
Ảnh hưởng của thời tiết và dịch bệnh là nguyên nhân dẫn đến thu nhập của một hợp tác xã trồng rau bị giảm dần trong năm 2021. Đoạn thẳng \(AB\) ở Hình 12 biểu thị số tiền (đơn vị: trăm triệu đồng) mà hợp tác xã đó thu được trong mỗi tháng của năm 2021.
a) Tính hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng \(AB\).
b) Biết cứ mỗi yến rau bán được thì hợp tác xã đó thu được 125 000 đồng. Hỏi hợp tác xã đó đã thu được bao nhiêu tấn rau trong tháng 11/2021 (làm tròn kết quả đến hàng đơn vị)?
Một ô tô đi từ bến xe Giáp Bát (Hà Nội) đến thành phố Vinh (Nghệ An) Với vận tốc 60 km/h. Hỏi sau t giờ ô tô đó cách trung tâm Hà Nội bao nhiêu kilômét? Biết rằng bến xe Giáp Bát cách trung tâm Hà Nội 7km và coi rằng trung tâm Hà Nội, bến xe Giáp Bát và thành phố Vinh nằm trên cùng một đường thẳng
Xét bài toán mở đầu
Một ô tô đi từ bến xe Giáp Bát (Hà Nội) đến thành phố Vinh (Nghệ An) Với vận tốc 60 km/h. Hỏi sau t giờ ô tô đó cách trung tâm Hà Nội bao nhiêu kilômét? Biết rằng bến xe Giáp Bát cách trung tâm Hà Nội 7km và coi rằng trung tâm Hà Nội, bến xe Giáp Bát và thành phố Vinh nằm trên cùng một đường thẳng
Viết công thức tính quãng đường S đi được của ô tô sau t giờ. Quãng đường s có phải là một hàm số của thời gian không
Viết công thức tính khoảng cách d từ vị trí của ô tô đến trung tâm Hà Nội sau t giờ
Từ kết quả của HĐ2, hãy hoàn thành bảng sau vào vở
|
t (giờ) |
1 |
2 |
3 |
4 |
5 |
|
d (km) |
? |
? |
? |
? |
? |
Trong hệ đo lường Anh - Mỹ, quãng đường thường được đo bằng dặm (mile) và 1 dặm bằng khoảng 1,609 km
a) Viết công thức để chuyển đổi x (km) sang y (dặm). Công thức tính y theo x này có phải là một hàm số bậc nhất của x không
b) Một ô tô chạy với vận tốc 55 dặm/ giờ trên một quãng đường có quy định vận tốc tối đa là 80km/h. Hỏi ô tô đó có vi phạm luật giao thông không?
Pi: Hàm số \(y = \frac{{x + 1}}{2}\) có phải là hàm số bậc nhất không?
Vuông: Đây là hàm số bậc nhất
Tròn: Không đúng, tớ nghĩ đây không phải hàm số bậc nhất.
Theo em, Vuông hay Tròn ai nói đúng? Vì sao?
a) y = 3x - 2;
b) y = -2x;
c) \(y = 2x^2 + 3\);
d) y = 3(x - 1);
e) y = 0x + 1.
Cho hàm số bậc nhất y=2x−1
Hoàn thành bảng giá trị sau vào vở
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y=2x−1 |
? |
? |
? |
? |
? |
Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b của chúng
a) y=0.x−5
b) y=1−3x
c) y=−0,6x
d) y= \(\sqrt 2 \)(x−1)+3
e) \(y = 2{{\rm{x}}^2} + 1\)
