Rút gọn biểu thức

a) \(\left( {5\sqrt {\frac{1}{5}}  - \frac{1}{2}\sqrt {20}  + \sqrt 5 } \right)\sqrt 5 \)

b) \(\left( {\sqrt {\frac{1}{7}}  - \sqrt {\frac{9}{7}}  + \sqrt 7 } \right):\sqrt 7 \)

c) \({\left( {\sqrt {\frac{2}{3}}  - \sqrt {\frac{3}{2}} } \right)^2}\)

d) \(\frac{{\sqrt {{{312}^2} - {{191}^2}} }}{{\sqrt {503} }}\)

e) \(\sqrt {27.{{\left( {1 - \sqrt 3 } \right)}^4}} :3\sqrt {15} \)

g) \(\frac{{\sqrt[3]{{135}}}}{{\sqrt[3]{5}}} - \sqrt[3]{{54}}.\sqrt[3]{4}\)

Rút gọn biểu thức \(A = \sqrt {1 + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {a + 1} \right)}^2}}}} \) với \(\left( {a > 0} \right)\)

Rút gọn các biểu thức sau:

a) \(\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}} \)

b) \(2\sqrt {{a^2}}  + 4a\) với a < 0

c) \(\sqrt {{a^2}}  + \sqrt {{{\left( {3 - a} \right)}^2}} \) với 0 < a < 3

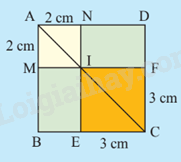
Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.

a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.

b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.

Rút gọn các biểu thức sau:

a) \(\sqrt {20}  - \sqrt 5 \)

b) \(\sqrt {32}  - \sqrt {18}  + \frac{4}{{\sqrt 2 }}\)

c) \(\left( {2 - \sqrt {10} } \right)\left( {\sqrt 2 - \sqrt 5 } \right)\)

Rút gọn các biểu thức sau:

a) \(\frac{2}{3}\sqrt {9{x^3}}  + 4x\sqrt {\frac{x}{4}}  - {x^2}\sqrt {\frac{1}{x}} \) với x > 0

b) \(\frac{{{a^2} - 5}}{{a + \sqrt {15} }}\) với a \( \ne  - \sqrt 5 \)

Rút gọn các biểu thức sau:

a) \(2\sqrt 3  - \sqrt {27} \)

b) \(\sqrt {45}  - \sqrt {20}  + \sqrt 5 \)

c) \(\sqrt {64a}  - \sqrt {18}  - a\sqrt {\frac{9}{a}}  + \sqrt {50} \) với a > 0

Tính

a) \(\left( {\sqrt {\frac{4}{3}}  + \sqrt 3 } \right)\sqrt 6 \)

b) \(\sqrt {18} :\sqrt 6  + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)

c) \({\left( {1 - 2\sqrt 5 } \right)^2}\)

Chứng minh rằng:

a) \(\frac{{a\sqrt b  - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a  + \sqrt b }} = a - b\) với a > 0; b > 0

b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a  + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a  - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1

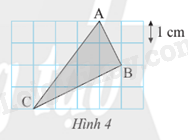
Tam giác ABC được vẽ trên ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC

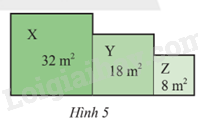
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.

Cho a = \(2\sqrt 3  + \sqrt 2 \), b = \(3\sqrt 2  - 2\sqrt 3 \). Rút gọn biểu thức \(\sqrt 3 a - \sqrt 2 b\), ta có kết quả

A. \(3\sqrt 6 \)

B. \( - \sqrt 6 \)

C. \(6\sqrt 3 \)

D. \(12 - \sqrt 6 \)

Rút gọn biểu thức \(\frac{1}{{2\sqrt a  + \sqrt 2 }} - \frac{1}{{2\sqrt a  - \sqrt 2 }}\) với \(a \ge 0\), \(a \ne \frac{1}{2}\), ta có kết quả

A. \(\frac{{\sqrt 2 }}{{1 - 2a}}\)

B. \(\frac{{\sqrt 2 }}{{2a - 1}}\)

C. \(\frac{{\sqrt a }}{{2a - 1}}\)

D. \(\frac{{\sqrt 2 }}{{1 - a}}\)

Tính \(\frac{{\sqrt 3  + \sqrt 2 }}{{\sqrt 3  - \sqrt 2 }} - \frac{{\sqrt 3  - \sqrt 2 }}{{\sqrt 3  + \sqrt 2 }}\).

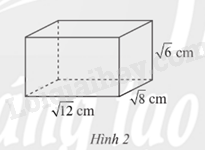
Cho hình hộp chữ nhật có chiều dài \(\sqrt {12} \)cm, chiều rộng\(\sqrt 8 \)cm, chiều cao \(\sqrt 6 \) như Hình 2.

a) Tính thể tích của hình hộp chữ nhật đó.

b) Tính diện tích xung quanh của hình hộp chữ nhật đó.

Hãy chép lại và hoàn thành Bảng 3.2. Em có nhận xét gì về giá trị của \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \)?

Rút gọn rồi tính giá trị các biểu thức sau:

a) \(\sqrt {9{{\left( {4 - 4x + {x^2}} \right)}^2}} \) tại \(x = \sqrt 2 \);

b) \(\sqrt {4{a^2}{{\left( {9{b^2} + 6b + 1} \right)}^2}} \) tại \(a =  - 2,b =  - \sqrt 3 \);

c) \({a^2}{b^2}.\sqrt {\frac{{9{b^4}}}{{25{a^6}}}} \) tại \(a =  - 3,b = \sqrt 5 \);

d) \(\frac{{\sqrt {3{x^6}{y^4}} }}{{\sqrt {27{x^2}{y^2}} }}\) tại \(x =  - 3,y = \sqrt 5 \).

Rút gọn các biểu thức sau (với giả thiết các biểu thức đều có nghĩa):

a) \(\frac{{6\sqrt 2  + 3}}{{1 + 2\sqrt 2 }}\);

b) \(\frac{{\sqrt {15}  - \sqrt 5 }}{{\sqrt 3  - 1}}\);

c) \(\frac{{m - 2\sqrt m }}{{2 - \sqrt m }}\);

d) \(\frac{{3x + \sqrt {xy} }}{{3\sqrt x  + \sqrt y }}\).

Rút gọn các biểu thức sau (giả thiết các biểu thức đều có nghĩa):

a) \(\left( {\frac{1}{{\sqrt a  - 1}} + \frac{1}{{a - \sqrt a }}} \right):\frac{{\sqrt a  + 1}}{{a - 2\sqrt a  + 1}}\);

b) \(\frac{{xy + y\sqrt x  + \sqrt x  + 1}}{{y\sqrt x  + 1}}\);

c) \(\frac{{\sqrt {{a^3}}  - \sqrt {{b^3}}  + \sqrt {{a^2}b}  - \sqrt {a{b^2}} }}{{\sqrt a  + \sqrt b }}\).

Rút gọn biểu thức \(A = \left( {\frac{{\sqrt {14}  - \sqrt 7 }}{{1 - \sqrt 2 }} + \frac{{\sqrt {15}  - \sqrt 5 }}{{1 - \sqrt 3 }}} \right)\left( {\sqrt 7  - \sqrt 5 } \right)\), ta thu được giá trị của A là

A. \( - 2\).

B. 2.

C. \( - 1\).

D. 1.

Giá trị của biểu thức \(\sqrt {{{\left( {4 - \sqrt 5 } \right)}^2}}  - \sqrt {6 - 2\sqrt 5 } \)   là:

Giá trị của biểu thức \(\sqrt {{{\left( {\sqrt 2  + \sqrt 5 } \right)}^2}}  - \sqrt {7 - 2\sqrt {10} } \).

Giá trị của biểu thức \(\sqrt {17 - 12\sqrt 2 }  + \sqrt {9 + 4\sqrt 2 } \).

Rút gọn biểu thức \(5\sqrt a  + 2\sqrt {\dfrac{a}{4}}  - a\sqrt {\dfrac{4}{a}}  - \sqrt {25a} \)  với \(a > 0\) ta được

Rút gọn biểu thức \(3\sqrt {8a}  + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}}  - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}}  - \sqrt {2a} \) với \(a > 0\) ta được:

Rút gọn biểu thức \(2\sqrt a  - \sqrt {9{a^3}}  + {a^2}\sqrt {\dfrac{{16}}{a}}  + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \) với $a > 0$ ta được 

Rút gọn biểu thức \(\left( {\dfrac{1}{2}\sqrt {\dfrac{a}{2}}  - \dfrac{3}{2}\sqrt {2a}  + \dfrac{4}{5}\sqrt {200a} } \right):\dfrac{1}{8}\) ta được:

Đẳng thức nào dưới đây là đúng?

Với \(a,b > 0\), đẳng thức nào dưới đây là đúng?

Chọn khẳng định đúng?

Chọn khẳng định đúng?