Tìm số nguyên tố p thỏa mãn mỗi điều kiện sau:
a) p + 1 cũng là số nguyên tố;
b) p +2 và p+4 đều là số nguyên tố;
c) p +2, p+6, p+14, p+18 đều là số nguyên tố.
Xét các trường hợp của p
Do p là số nguyên tố nên p là số tự nhiên lớn hơn 1
a) Ta xét 2 trường hợp sau:
+ Trường hợp 1: p=2 thì p+1 =2+1=3 là số nguyên tố( thỏa mãn)
+ Trường hợp 2: p > 2 thì p là số lẻ lớn hơn 2 nên p+1 là số chẵn( không là số nguyên tố) (loại)
Vậy p=2
b) Ta xét 3 trường hợp sau:
+ Trường hợp 1: p=2 thì p+2=4(không là số nguyên tố)(loại)
+ Trường hợp 2: p=3 thì p+2=5; p+4= 7 đều là số nguyên tố (thỏa mãn)
+ Trường hợp 3: p>3 ,mà p là số nguyên tố nên p chia cho 3 dư 1 hoặc dư 2
- Nếu p chia cho 3 dư 1 thì p+2 chia hết cho 3 nên p+2 không là số nguyên tố(loại)
- Nếu p chia cho 3 dư 2 thì p+4 chia hết cho 3 nên p+4 không là số nguyên tố(loại)
Vậy p = 3
c) Ta xét 4 trường hơp sau:
+ Trường hợp 1: p=2 thì p+2=4(không là số nguyên tố)(loại)
+ Trường hợp 2: p=3 thì p+6=9(không là số nguyên tố)(loại)
+ Trường hợp 3: p=5 thì p+2=7; p+6=11; p+14=19; p+18=23 đều là các số nguyên tố(thỏa mãn)
+ Trường hợp 4: p>5, mà p là số nguyên tố thì p chia cho 5 có thể dư 1,2,3,4.
- Nếu p chia cho 5 dư 1 thì p+4 chia hết cho 5 nên không là số nguyên tố(loại)
- Nếu p chia cho 5 dư 2 thì p+18 chia hết cho 5 nên không là số nguyên tố(loại)
- Nếu p chia cho 5 dư 3 thì p+2 chia hết cho 5 nên không là số nguyên tố(loại)
- Nếu p chia cho 5 dư 1 thì p+14 chia hết cho 5 nên không là số nguyên tố(loại)
Vậy p=5

Các bài tập cùng chuyên đề
Phân tích các số sau ra thừa số nguyên tố: 70; 115.
Kết quả phân tích các số 120; 102 ra thừa số nguyên tố của bạn Nam như sau:
120 = 2.3.4.5 ; 102 = 2.51.
Theo em, kết quả của Nam đúng hay sai? Nếu sai, em hãy sửa lại cho đúng.
Hãy phân tích A ra thừa số nguyên tố: A = 44.95
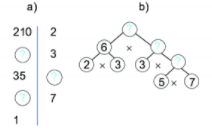
Tìm các số còn thiếu trong các sơ đồ phân tích một số ra thừa số nguyên tố sau:
Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau và có nhiều hơn 1 người trong mỗi nhóm. Hỏi mỗi nhóm có thể có bao nhiêu người?
Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hằng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người gồm 1 sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng sao cho mỗi hàng có số người như nhau?
Thực hiện phép tính sau rồi phân tích kết quả ra thừa số nguyên tố:
a) 142 + 52 + 22;
b) 400 : 5 + 40
Hãy phân tích các số A, B ra thừa số nguyên tố:
A = \(4^2.6^3\)
B =\(9^2.15^2\)
Bạn Việt phân tích số 60 ra thừa số nguyên tố và cho kết quả 60 = 3. 4. 5. Kết quả của Việt đúng hay sai? Nếu sai, em hãy sửa lại cho đúng.
Phân tích các số sau ra thừa số nguyên tố theo sơ đồ cột:
a) 36;
b) 105.
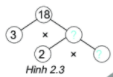
Tìm các số còn thiếu trong phân tích số 18 ra thừa số nguyên tố theo sơ đồ cây ở hình 2.3.
Tìm các số còn thiếu trong phân tích số 30 ra thừa số nguyên tố theo sơ đồ cột ở hình bên.

Phân tích mỗi số sau ra thừa số nguyên tố rồi cho biết mỗi số chia hết cho các số nguyên tố nào?
a) 80; b) 120; c) 225; d) 400.
Phân tích mỗi số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số.
a) 30; b) 225;
c) 210; d) 242.
Cho số a = 23.32.7. Trong các số 4, 7, 9, 21, 24, 34, 49, số nào là ước của a?
Phân tích số 60 ra thừa số nguyên tố theo cột dọc.
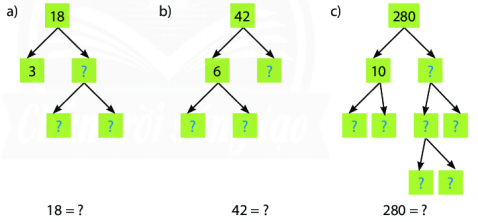
Tìm các số tự nhiên lớn hơn 1 để thay thế dấu trong ô vuông ở mỗi sơ đồ cây dưới đây, rồi viết gọn dạng phân tích ra thừa số nguyên tố của mỗi số 18, 42, 280 bằng cách dùng luỹ thừa.
Phân tích các số nguyên ra thừa số nguyên tố: 45, 78, 270, 299
a) Biết \(400 = {2^4}{.5^2}\). Hãy viết 800 thành tích các thừa số nguyên tố
b) Biết \(320 = {2^6}.5\). Hãy viết 3200 thành tích các thừa số nguyên tố
a) Biết \(2700 = {2^2}{.3^3}{.5^2}\). Hãy viết 270 và 900 thành tích các thừa số nguyên tố
b) Biết \(3600 = {2^4}{.3^2}{.5^2}\). Hãy viết 180 và 600 thành tích các thừa số nguyên tố
Hãy chỉ ra 2 số tự nhiên mà mỗi số đó có đúng 3 ước nguyên tố
Phân tích số 84 ra thừa số nguyên tố rồi tìm tập hợp các ước số của nó.
Phân tích các số sau ra thừa số nguyên tố:
a) 51;
b) 76;
c) 225;
d) 1800.
Viết số 12 thành tích của các thừa số nguyên tố.
Phân tích số 40 ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”.
Phân tích số 450 ra thừa số nguyên tố.
Phân tích các số sau ra thừa số nguyên tố bằng hai cách “theo cột dọc” và dùng “sơ đồ cây”:
a) 154;
Phân tích các số sau ra thừa số nguyên tố bằng hai cách “theo cột dọc” và dùng “sơ đồ cây”:
b) 187;
Phân tích các số sau ra thừa số nguyên tố bằng hai cách “theo cột dọc” và dùng “sơ đồ cây”:
c) 630.
Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số đó:
a) 38;
b) 75;
c) 100.







Danh sách bình luận