Các phát biểu sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng:
a) \(\sqrt {36} \) ∈ Q
b) \(\sqrt 7 \) ∈ R
c) 0,23 \( \notin \) R
d) \( - \sqrt 3 \) ∈ R
Đầu tiên ta phải khai căn sau đó sử dụng định nghĩa của các tập hợp vô tỉ, hữu tỉ để tìm phát biểu đúng, sai
a) Ta có 62 = 36 nên \(\sqrt {36} \)=6 là số hữu tỉ suy ra \(\sqrt {36} \)∈Q. Do đó a) đúng.
b) Ta có: \(\sqrt 7 \) = 2,645751311 là số thập phân vô hạn không tuần hoàn nên \(\sqrt 7 \) là số vô tỉ, mà số vô tỉ là số thực suy ra \(\sqrt 7 \) ∈R. Do đó b) đúng.
c) Ta có: 0,23 = \(\dfrac{{23}}{{100}}\) (trong đó 23; 100 ∈ ℤ và 100 ≠ 0) là số hữu tỉ mà số hữu tỉ là số thực suy ra 0,23∈R. Do đó c) sai.
d) Ta có: \( - \sqrt 3 \) = -1,7320508075... là số thập phân vô hạn không tuần hoàn nên \( - \sqrt 3 \) là số vô tỉ, mà số vô tỉ là số thực suy ra \( - \sqrt 3 \)∈R. Do đó d) đúng

Các bài tập cùng chuyên đề
Xét tập hợp \(A = \left\{ {7,1; - 2,(61);0;5,14;\frac{4}{7};\sqrt {15} ; - \sqrt {81} } \right\}\). Bằng cách liệt kê phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ thuộc tập A.
Hãy thay mỗi ? bằng kí hiệu \( \in \) hoặc \( \notin \) để có phát biểu đúng.
Các phát biểu sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.
\(\begin{array}{l}a)\,\sqrt 9 \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,b)\,\sqrt 5 \in \mathbb{R};\,\,\,\\c)\,\frac{{11}}{9} \notin \mathbb{R};\,\,\,\,\,\,\,\,\,\,\,\,d)\,\, - \sqrt 7 \in \mathbb{R}.\end{array}\)
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu a \( \in \) Z thì a \( \in \) R
b) Nếu a \( \in \) Q thì a \( \in \) R
c) Nếu a \( \in \) R thì a \( \in \) Z
d) Nếu a \( \in \) R thì a \( \notin \) Q
Cách nào đúng trong các cách viết sau:
-
A.
\( - 10 \in \mathbb{N}\);
-
B.
\(0 \in \mathbb{N}*\);
-
C.
\(\frac{{ - 3}}{7} \in \mathbb{Z}\);
-
D.
\(- 5 \in \mathbb{Q}\).
Chọn kí hiệu “\( \in \)”, “\( \notin \)” thích hợp cho ?:
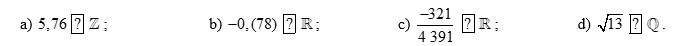
Chọn các từ “số thực”, “số hữu tỉ”, “số vô tỉ” thích hợp cho ?

Chọn câu trả lời đúng?
-
A.
\( - 5 \in \mathbb N\)
-
B.
\( - \frac{5}{7} \in \mathbb Z\)
-
C.
\( - \frac{4}{7} \not \in \mathbb Q\)
-
D.
\( \frac{3}{5} \in \mathbb Q\)
Kí hiệu \(\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{I},\mathbb{R}\) theo thứ tự là tập hợp các số tự nhiên, tập hợp các số nguyên, tập hợp các số hữu tỉ, tập hợp các số vô tỉ và tập hợp các số thực. Khẳng định nào sau đây là sai?
A. Nếu \(x \in \mathbb{N}\) thì \(x \in \mathbb{Z}\)
B. Nếu \(x \in \mathbb{R},x \notin \mathbb{Q}\) thì \(x \in I\)
C. \(1 \in \mathbb{R}\)
D. Nếu \(x \notin I\) thì x viết được thành số thập phân hữu hạn.
Hãy thay dấu bằng kí hiệu ∈ hoặc ∉ để có phát biểu đúng.
3,9 ? Z
29% ? Q
\(\sqrt 7 \) ? Q
\( - \dfrac{4}{{99}}\) ? Q
\(\sqrt 3 \) ? I.
\(\sqrt 5 \)? R
\(\pi\) ? I
Hãy cho biết tính đúng, sai của các khẳng định sau:
a) \(\sqrt 4 \);\(\sqrt 9 \);\(\sqrt {25} \) là các số vô tỉ;
b) Số vô tỉ không phải là số thực;
c) \( - \dfrac{1}{2};\dfrac{2}{3}; - 0,45\) là các số hữu tỉ;
d) Số 0 là số vô tỉ;
e) 0,1; 0; 9; 99% là các số hữu tỉ.
Xét tập hợp \(A = \left\{ {7,1; - 2,\left( {61} \right);0,5;14;\frac{4}{7};\sqrt {15} ; - \sqrt {81} } \right\}\)
Bằng cách liệt kê các phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ thuộc tập A.
Khẳng định nào sau đây là sai?
-
A.
\( - 0,5 \in \mathbb{Q}\);
-
B.
\( - \frac{3}{2} \notin \mathbb{Z}\);
-
C.
\( - 1 \in \mathbb{N}\)
-
D.
\( - \frac{3}{2} \in \mathbb{Q}\).
Trong các khẳng định sau, khẳng định nào đúng?
-
A.
\( - 9 \in \mathbb{N}\).
-
B.
\(\frac{7}{3} \in \mathbb{Z}\).
-
C.
\(1,2 \notin \mathbb{R}\).
-
D.
\(\frac{{ - 5}}{2} \in \mathbb{Q}\).
Khẳng định nào sau đây sai?
-
A.
\( - 5 \in \mathbb{Q}\).
-
B.
\(\frac{{ - 3}}{5} \notin \mathbb{Z}\).
-
C.
\(6,7 \in \mathbb{N}\).
-
D.
\(\frac{3}{4} \in \mathbb{Q}\).
Khẳng định nào sau đây đúng?
-
A.
\(5 \in \mathbb{Q}\).
-
B.
\(\frac{{ - 3}}{2} \in \mathbb{Z}\).
-
C.
\( - 1,5 \in \mathbb{N}\).
-
D.
\(\frac{{ - 3}}{2} \notin \mathbb{Q}\).
Chọn khẳng định đúng:
-
A.
\( - 7 \in \mathbb{N}\).
-
B.
\(\frac{2}{3} \in \mathbb{Z}\).
-
C.
\(\frac{{ - 2}}{9} \notin \mathbb{Q}\).
-
D.
\(\frac{1}{{10}} \in \mathbb{Q}\).
Tìm \(x\):
a) \(x - \frac{1}{4} = \frac{2}{3}\)
b) \(\frac{1}{4} + \frac{3}{4}x = \frac{{ - 13}}{8}\)
c) \(\left| {\frac{3}{4}x - \frac{1}{2}} \right| + {\left( {\frac{{ - 1}}{2}} \right)^2} = \sqrt {\frac{4}{9}} \)
Tìm x, biết:
a) \(x + \sqrt {36} = 5\)
b) \(\left| {x - 2} \right| - \frac{3}{5} = \frac{1}{2}\)
Trong các khẳng định sau, khẳng định đúng là:
-
A.
\(3 \in \mathbb{Q}\).
-
B.
\(1\frac{1}{5} \notin \mathbb{Q}\).
-
C.
\(\frac{2}{3} \in \mathbb{N}\).
-
D.
\( - \frac{1}{7} \in \mathbb{Z}\).
Chọn khẳng định đúng:
-
A.
\(\sqrt 3 \in \mathbb{N}\).
-
B.
\(\sqrt 3 \in \mathbb{Z}\).
-
C.
\(\frac{2}{3} \in \mathbb{Q}\).
-
D.
\( - 9 \in {\mathbb{N}^*}\).
A. \(\pi \in \mathbb{N}\).
B. \(3,(5) \in \mathbb{Q}\).
C. \( - 13 \notin \mathbb{R}\).
D. \(0 \in I\).
A. \(\sqrt {144} \).
B. \(2,\left( 3 \right)\).
C. \( - 1,2345\).
D. \(\pi = 3,141592653589...\).

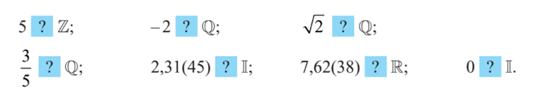






Danh sách bình luận