Đề bài
Gọi $M$ và $N$ lần lượt là điểm biểu diễn của các số phức ${z_1};{z_2}$ khác $0$. Khi đó khẳng định nào sau đây sai ?
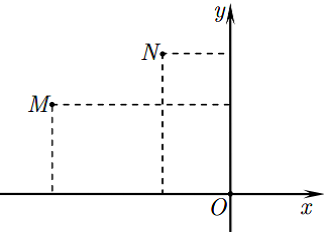
-
A.
$\left| {{z_2}} \right| = ON$
-
B.
$\left| {{z_1} - {z_2}} \right| = MN$
-
C.
$\left| {{z_1} + {z_2}} \right| = MN$
-
D.
$\left| {{z_1}} \right| = OM$
Phương pháp giải
Dựa vào đồ thị đề bài cho để tìm ra phương án sai.
Lời giải của GV Loigiaihay.com
Ta có: $\left| {{z_1} + {z_2}} \right| = MN$ là khẳng định sai vì dựa vào đồ thị ta có: $\left| {{z_1} - {z_2}} \right| = MN$
Đáp án : C








Danh sách bình luận