Sắp xếp các số sau theo thứ tự giảm dần:
a) \(\dfrac{2}{{15}};{\rm{ }}\dfrac{2}{3};{\rm{ }} - \dfrac{7}{8};{\rm{ }}\dfrac{5}{6};{\rm{ }}\dfrac{{ - 7}}{9}\);
b) \(\dfrac{{19}}{{22}};{\rm{ }}0,5;{\rm{ }} - \dfrac{1}{4};{\rm{ }} - 0,05;{\rm{ }}2\dfrac{1}{6}\).
So sánh các cặp số với nhau để sắp xếp chúng theo thứ tự giảm dần.
a) Ta có:
\(\dfrac{2}{{15}};{\rm{ }}\dfrac{2}{3};{\rm{ }}\dfrac{5}{6}{\rm{ > 0 > }} - \dfrac{7}{8};{\rm{ }}\dfrac{{ - 7}}{9}\).
\( - \dfrac{7}{8} = \dfrac{{ - 7}}{8} < \dfrac{{ - 7}}{9}\);
\(\dfrac{2}{{15}} = \dfrac{8}{{60}};{\rm{ }}\dfrac{2}{3} = \dfrac{{40}}{{60}};{\rm{ }}\dfrac{5}{6}{\rm{ = }}\dfrac{{50}}{{60}}{\rm{ }}\) mà \(\dfrac{8}{{60}} < \dfrac{{40}}{{60}} < \dfrac{{50}}{{60}}\) nên \(\dfrac{2}{{15}} < \dfrac{2}{3} < \dfrac{5}{6}\).
Suy ra: \(\dfrac{5}{6}{\rm{ > }}\dfrac{2}{3}{\rm{ > }}\dfrac{2}{{15}}{\rm{ > }}\dfrac{{ - 7}}{9}{\rm{ > }}\,{\rm{ }} - \dfrac{7}{8}\).
Các số theo thứ tự giảm dần là: \(\dfrac{5}{6};{\rm{ }}\dfrac{2}{3}{\rm{; }}\dfrac{2}{{15}};{\rm{ }}\dfrac{{ - 7}}{9};\,{\rm{ }} - \dfrac{7}{8}\).
b) Cách 1:
Ta có:
\(\dfrac{{19}}{{22}};{\rm{ }}0,5;{\rm{ }}2\dfrac{1}{6}{\rm{ > 0 > }} - \dfrac{1}{4};{\rm{ }} - 0,05\).
\( - \dfrac{1}{4} = - 0,25 < - 0,05\).
\(\dfrac{{19}}{{22}} = \dfrac{{57}}{{66}};{\rm{ }}0,5 = \dfrac{1}{2} = \dfrac{{33}}{{66}};{\rm{ }}2\dfrac{1}{6}{\rm{ = }}\dfrac{{13}}{6}{\rm{ = }}\dfrac{{143}}{{66}}{\rm{ }}\)mà \(\dfrac{{33}}{{66}}{\rm{ < }}\dfrac{{57}}{{66}}{\rm{ < }}\dfrac{{143}}{{66}}{\rm{ }}\)nên \(0,5{\rm{ < }}\dfrac{{19}}{{22}}{\rm{ < 2}}\dfrac{1}{6}\).
Suy ra: \({\rm{ }}2\dfrac{1}{6}{\rm{ > }}\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{ > }}0,5{\rm{ > }} - 0,05{\rm{ > }} - \dfrac{1}{4}\).
Các số theo thứ tự giảm dần là: \({\rm{ }}2\dfrac{1}{6};\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{; }}0,5;{\rm{ }} - 0,05;{\rm{ }} - \dfrac{1}{4}\).
Cách 2:
\(\dfrac{{19}}{{22}};{\rm{ }}0,5;{\rm{ }}2\dfrac{1}{6}{\rm{ > 0 > }} - \dfrac{1}{4};{\rm{ }} - 0,05\).
\( - \dfrac{1}{4} = - 0,25 < - 0,05\).
\(0,5=\dfrac{11}{22}<\dfrac{19}{22}<1<2\dfrac{1}{6}\)
Ta được:
\({\rm{ }}2\dfrac{1}{6}{\rm{ > }}\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{ > }}0,5{\rm{ > }} - 0,05{\rm{ > }} - \dfrac{1}{4}\).
Các số theo thứ tự giảm dần là: \({\rm{ }}2\dfrac{1}{6};\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{; }}0,5;{\rm{ }} - 0,05;{\rm{ }} - \dfrac{1}{4}\).

Các bài tập cùng chuyên đề
Viết các số hữu tỉ dưới dạng phân số rồi so sánh:
a) -1,5 và \(\frac{5}{2}\); b) -0,375 và \( - \frac{5}{8}\)
Biểu diễn hai số hữu tỉ -1,5 và \(\frac{5}{2}\) trên trục số. Em hãy cho biết điểm -1,5 nằm trước hay nằm sau điểm \(\frac{5}{2}\) trên trục số.
Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn.
\(5\frac{1}{4}; - 2;3,125; - \frac{3}{2}.\)
Em hãy giải bài toán mở đầu.
Chỉ số WHtR (Waist to Height Ratio) của một người trưởng thành, được tính bằng tỉ số giữa số đo vòng bụng và số đo chiều cao (cùng một đơn vị đo). Chỉ số này được coi là một công cụ đo lường sức khỏe hữu ích vì có thể dự báo được nguy cơ béo phì, mắc bệnh tim mạch,… Bảng bên cho biết nguy cơ thừa cân, bép phì của một người đàn ông trưởng thành dựa vào chỉ số WHtR.
(Theo hospitamedia.com)
Ông An cao 180 cm, vòng bụng 108 cm.
Ông Chung cao 160 cm, vòng bụng 70 cm.
Theo em, nếu tính theo chỉ số WHtR, sức khỏe của ông An hay ông Chung tốt hơn?
So sánh:
a) -2,5 và -2,125;
b) \( - \frac{1}{{10000}}\) và \(\frac{1}{{23456}}\)
Tuổi thọ trung bình dự kiến của những người sinh năm 2019 ở một số quốc gia được cho trong bảng sau:
|
Quốc gia |
Australia |
Pháp |
Tây Ban Nha |
Anh |
Mỹ |
|
Tuổi thọ trung bình dự kiến |
83 |
82,5 |
\(83\frac{1}{5}\) |
\(81\frac{2}{5}\) |
\(78\frac{1}{2}\) |
(Theo Báo cáo của Tổ chức Y tế Thế giới, 2020)
Sắp xếp các quốc gia theo tuổi thọ trung bình dự kiến từ nhỏ đến lớn.
So sánh:
a) \(\frac{{123}}{7}\) và 17,75
b) \( - \frac{{65}}{9}\) và -7,125.
Bảng sau cho biết các điểm đông đặc và điểm sôi của sáu nguyên tố được gọi là khí hiếm.
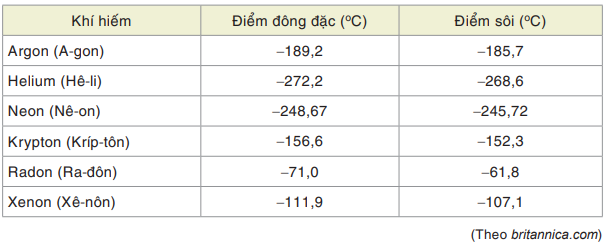
a) Khí hiếm nào có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton?
b) Khí hiếm nào có điểm sôi lớn hơn điểm sôi của Argon?
c) Hãy sắp xếp các khí hiếm theo thứ tự điểm đông đặc tăng dần;
d) Hãy sắp xếp các khí hiếm theo thứ tự điểm sôi giảm dần.
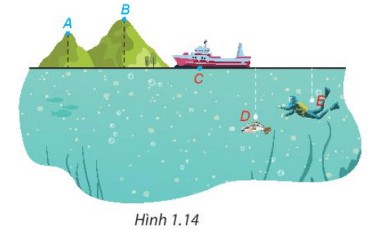
Hình 1.14 mô phỏng vị trí của năm điểm A,B,C,D,E so với mực nước biển. Biết rằng độ cao (tính theo đơn vị kilomet) so với mực nước biển của mỗi điểm là một trong các số sau:
\(\frac{{33}}{{12}};\frac{{79}}{{30}}; - \frac{{25}}{{12}}; - \frac{5}{6};0.\)
a) So sánh hai phân số \(\frac{2}{9}\) và \( - \frac{5}{9}\).
b) Trong mỗi trường hợp sau, nhiệt độ nào cao hơn?
i) \({0^o}C\) và \( - 0,{5^o}C;\) ii) \( - {12^o}C\) và \( - {7^o}C\).
Cho các số hữu tỉ: \(\frac{{ - 7}}{{12}};\,\frac{4}{5};\,5,12;\, - 3;\,\frac{0}{{ - 3}};\, - 3,75.\)
a) So sánh \(\frac{{ - 7}}{{12}}\) với \( - 3,75\); \(\frac{0}{{ - 3}}\) với \(\frac{4}{5}\).
b) Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
\(\frac{5}{{12}};\, - \frac{4}{5};\,2\frac{2}{3};\, - 2;\,\frac{0}{{234}};\, - 0,32.\)
b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.
So sánh các cặp số hữu tỉ sau:
a) \(\frac{2}{{ - 5}}\) và \(\frac{{ - 3}}{8}\)
b) \( - 0,85\) và \(\frac{{ - 17}}{{20}}\);
c) \(\frac{{ - 137}}{{200}}\) và \(\frac{{37}}{{ - 25}}\)
d) \( - 1\frac{3}{{10}}\) và \(-\left( {\frac{{ - 13}}{{ - 10}}} \right)\).
So sánh các cặp số hữu tỉ sau:
a) \(\frac{{ - 2}}{3}\) và \(\frac{1}{{200}}\);
b) \(\frac{{139}}{{138}}\) và \(\frac{{1375}}{{1376}}\);
c) \(\frac{{ - 11}}{{33}}\) và \(\frac{{25}}{{ - 76}}\).
Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.
a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico? Giải thích.
b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên? Giải thích.
So sánh:
a) \( - \frac{1}{3}\) và \(\frac{{ - 2}}{5}\)
b) 0,125 và 0,13
c) -0,6 và \(\frac{{ - 2}}{3}\)
So sánh:
a) -3,23 và -3,32
b) \( - \frac{7}{3}\) và -1,25
Giả sử hai điểm a, b lần lượt biểu diễn hai số nguyên a,b trên trục số nằm ngang. Với a < b, nêu nhận xét về vị trí của điểm a so với điểm b trên trục số đó.
So sánh:
a) \(2,4\) và \(2\frac{3}{5}\);
b) \( - 0,12\) và \( - \frac{2}{5}\)
c) \(\frac{{ - 2}}{7}\) và \( - 0,3\).
a) Sắp xếp các số sau theo thứ tự tăng dần: \(\frac{{ - 3}}{7};\,0,4;\, - 0,5;\,\frac{2}{7}\).
b) Sắp xếp các số sau theo thứ tự giảm dần: \(\frac{{ - 5}}{6};\, - 0,75;\, - 4,5;\, - 1\).
Cô Hạnh dự định xây tầng hầm cho ngôi nhà của gia đình. Một công ty tư vấn xây dựng đã cung cấp cho cô Hạnh lựa chọn một trong sáu số đo chiều cao của tầng hầm như sau: 2,3 m; 2,35 m; 2,4 m; 2,55 m; 2,5 m; 2,75 m. Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn \(\frac{{13}}{5}\)m để đảm bảo ánh sáng, thoáng đãng, cân đối về kiến trúc và thuận tiện trong sử dụng. Em hãy giúp cô Hạnh chọn đúng số đo chiều cao của tầng hầm.
So sánh các số hữu tỉ sau:
a) \( - \dfrac{{57}}{{2021}}\) và \(\dfrac{1}{{6345}}\);
b) \(\dfrac{{ - 19}}{{35}}\) và \(\dfrac{{ - 13}}{{21}}\);
c) \(\dfrac{6}{{73}}\) và \(\dfrac{9}{{82}}\).
Máy ảnh thường có nhiều tốc độ màn trập (tức khoảng thời gian mà màn trập mở cửa). Tốc độ màn trập tính bằng giây, thường là \(\dfrac{1}{{125}};\dfrac{1}{{15}};0,125;\dfrac{1}{{60}};0,004;\dfrac{1}{4}\). Hãy sắp xếp các tốc độ này từ nhanh nhất đến chậm nhất.
Chỉ ra hai phân số có mẫu số bằng 7, lớn hơn \( \dfrac{- 3}{8}\) và nhỏ hơn \( \dfrac{- 1}{8}\).
Bảng sau thống kê thành tích ghi bàn của cầu thủ bóng đá Lionel Messi cho câu lạc bộ FC Barcelona tại giải bóng đá vô địch quốc gia La Liga của Tây Ban Nha trong 5 mùa giải gần đây.
|
Mùa giải |
Số bàn thắng |
Số trận đấu |
|
2020-2021 |
30 |
35 |
|
2019-2020 |
25 |
33 |
|
2018-2019 |
36 |
34 |
|
2017-2018 |
34 |
36 |
|
2016-2017 |
37 |
34 |
Biết hiệu suất ghi bàn được tính bằng tỉ số giữa số bàn thắng và số trận đấu. Em hãy sắp xếp hiệu suất ghi bàn của Messi từ bé đến lớn và cho biết mùa giải nào thì Messi ghi bàn tốt nhất.
a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
\(\dfrac{5}{{14}}\); \( - \dfrac{3}{5}\); \(1\dfrac{2}{5}\); -3; \(\dfrac{0}{{176}}\); -0,72
b) Hãy sắp xếp các số trên theo thứ tự từ bé đến lớn.
So sánh các cặp số hữu tỉ sau:
a) \(\dfrac{2}{{ - 3}}\) và \(\dfrac{{ - 3}}{5}\)
b) 0,65 và \(\dfrac{{13}}{{20}}\)
c) - 4,85 và - 3,48
d) \( - 1\dfrac{2}{9}\) và \( - \left( {\dfrac{{ - 11}}{{ - 9}}} \right)\)
So sánh các cặp số hữu tỉ sau:
a) \(\dfrac{{ - 2}}{7}\) và \(\dfrac{1}{{300}}\)
b) \(\dfrac{{237}}{{236}}\)và \(\dfrac{{2385}}{{2386}}\)
c) \(\dfrac{{ - 22}}{{33}}\)và \(\dfrac{{50}}{{ - 77}}\)
Ở vòng 1 cuộc thi tìm hiểu về bảo vệ môi trường, bạn Huy đã trả lời được 92% số câu trắc nghiệm. Ở vòng 2, bạn Huy đã trả lời đúng được 27 câu trong số 30 câu trắc nghiệm. Trong hai vòng thi, vòng nào bạn Huy làm bài tốt hơn?
Mực nước trong một cái ao so với mặt đất đo được trong các tháng được cho bởi bảng sau:

a) Trong các tháng trên tháng nào mực nước trong hồ cạn nhất? Giải thích.
b) Trong các tháng trên tháng nào hồ đầy nước nhất? Giải thích.








Danh sách bình luận