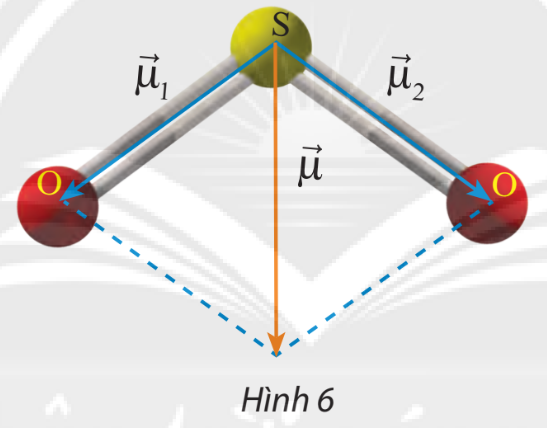
Phân tử sulfur dioxide \((S{O_2})\) có cấu tạo hình chữ V, góc liên kết \(\widehat {OSO}\) gần bằng \(120^\circ \). Người ta biểu diễn sự phân cực giữa nguyên tử S và nguyên tử O bằng các vectơ \(\overrightarrow {{\mu _1}} \)và \(\overrightarrow {{\mu _2}} \) có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng\(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} \) được dùng để biểu diễn sự phân cực của cả phân tử \(\)SO2. Tính độ dài của \(\overrightarrow \mu \).
Sử dụng kết quả của ví dụ 4 trang 101 \({c^2} = {a^2} + {b^2} - 2bc.\cos C\)
Từ điểm cuối của vectơ \(\overrightarrow {{\mu _1}} \) vẽ vectơ \(\overrightarrow {{\mu _3}} = \overrightarrow {{\mu _2}} \)
Suy ra \(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} \Rightarrow \left| {\overrightarrow \mu } \right| = \left| {\overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} } \right|\)
Ta có: \(\left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _2}} } \right) = 120^\circ \Rightarrow \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right) = 60^\circ \)
\( \Rightarrow {\left| {\overrightarrow \mu } \right|^2} = {\left| {\overrightarrow {{\mu _1}} } \right|^2} + {\left| {\overrightarrow {{\mu _3}} } \right|^2} - 2\left| {\overrightarrow {{\mu _1}} } \right|\left| {\overrightarrow {{\mu _3}} } \right|\cos \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right)\)
\( = 1,{6^2} + 1,{6^2} - 2.1,6.1,6.\cos 60^\circ = \frac{{64}}{{25}}\)
\( \Rightarrow \left| {\overrightarrow \mu } \right| = \sqrt {\frac{{64}}{{25}}} = 1,6\)
Vậy độ dài của \(\overrightarrow \mu \) là 1,6 đơn vị

Các bài tập cùng chuyên đề
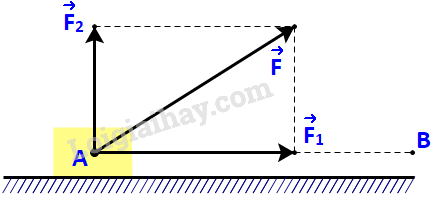
Một lực \(\overrightarrow F \) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực \(\overrightarrow F \) được phân tích thành hai lực thành phần là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) \((\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \;).\)
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow F \) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
b) Giả sử các lực thành phần \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow F \) và lực \(\overrightarrow {{F_1}} \).
Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \)
b) Tìm tọa độ của H.
c) Giải tam giác ABC.
Cho ba vectơ \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
a) Tính \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right),\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \) theo tọa độ của các vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w .\)
b) So sánh \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right)\) và \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) So sánh \(\;\overrightarrow u .\overrightarrow v \) và \(\overrightarrow v .\overrightarrow u \)
Chứng minh rằng với hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \), ta có:
\(\begin{array}{l}{(\overrightarrow a + \overrightarrow b )^2} = {\overrightarrow a ^2} + 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}\\{(\overrightarrow a - \overrightarrow b )^2} = {\overrightarrow a ^2} - 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}\\(\overrightarrow a - \overrightarrow b )(\overrightarrow a + \overrightarrow b ) = {\overrightarrow a ^2} - {\overrightarrow b ^2}\end{array}\)
Cho tam giác ABC. Chứng minh: \(A{B^2} + \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} = 0\)
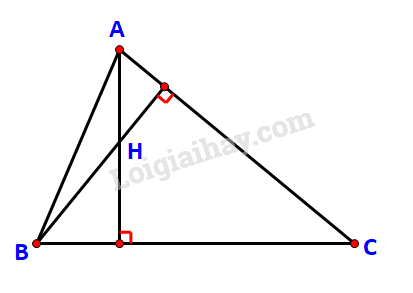
Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng:
a) \(\overrightarrow {AB} .\overrightarrow {AH} = \overrightarrow {AC} .\overrightarrow {AH} \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {HB} .\overrightarrow {BC} \)
Cho hai vectơ \(\overrightarrow i ,\overrightarrow j \) vuông góc có cùng độ dài bằng 1.
a) Tính \({\left( {\overrightarrow i + \overrightarrow j } \right)^2};{\left( {\overrightarrow i - \overrightarrow j } \right)^2};\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right)\).
b) Cho \(\overrightarrow a = 2\overrightarrow i + 2\overrightarrow j ,\overrightarrow b = 3\overrightarrow i - 3\overrightarrow j \). Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) và tính góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cho tứ giác ABCD. Biểu thức \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {BC} .\overrightarrow {CD} + \overrightarrow {CA} .\overrightarrow {CD} \) bằng:
A. CD²
B. 0
C. \(\overrightarrow 0 \)
D. 1
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Khẳng định nào sau đây là đúng?
A. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)
B. \(\overrightarrow a .\overrightarrow b = 0\)
C. \(\overrightarrow a .\overrightarrow b = - 1\)
D. \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)







Danh sách bình luận