Cho tam giác ABC
a) Xác định các điểm M, N, P thỏa mãn: \(\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA} \)
b) Biểu thị mỗi vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {BC} ,\overrightarrow {BA} \)
c) Chứng minh ba điểm M, N, P thẳng hàng
a) Xác định hướng và tỉ số độ dài
\(\overrightarrow {MB} = k.\overrightarrow {BC} \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\frac{{BC}}{{MB}} = k\)
b) Phân tích \(\overrightarrow {MN}\) theo hai vecto \(\overrightarrow {MB}, \overrightarrow {NB}\)
c) \(M,N,P\) thẳng hàng \( \Leftrightarrow \overrightarrow {MN} = k.\overrightarrow {MP} \) \(\left( k \in {\mathbb Z}^* \right)\)
a) Ta có:
+) \(\overrightarrow {MB} = \dfrac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\dfrac{{BC}}{{MB}} = 2\)
\( \Rightarrow M\) nằm ngoài đoạn thẳng BC sao cho \(MB = \dfrac{1}{2}BC\)
+) \({\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \dfrac{1}{4}\overrightarrow {AB} }\)
\( \Rightarrow N\) thuộc đoạn thẳng AB và \(NB=\dfrac{{1}}{{4}} AB\)
+) \(\overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0 \)
\( \Rightarrow P\) là trung điểm của CA
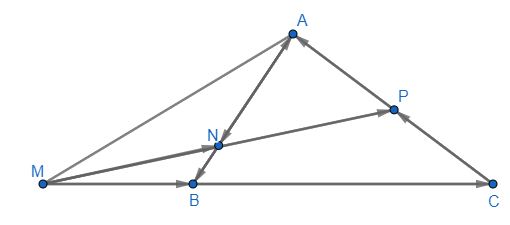
b) \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} \)
\(\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}\)
c) Ta có:
\(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ;\) \(\overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \)
\( \Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN} \)
Vậy \(M,N,P\) thẳng hàng

Các bài tập cùng chuyên đề
Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
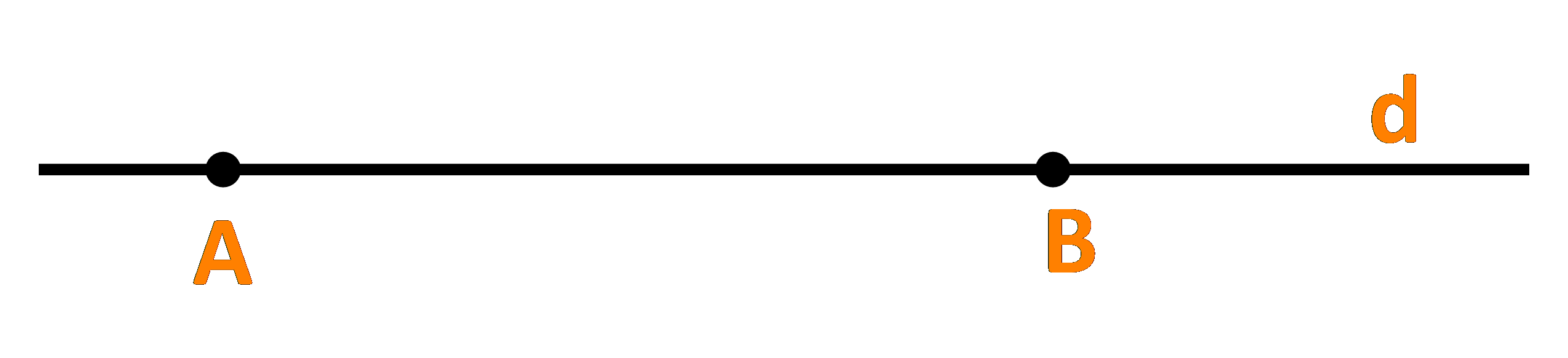
\( - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) có mối quan hệ gì?
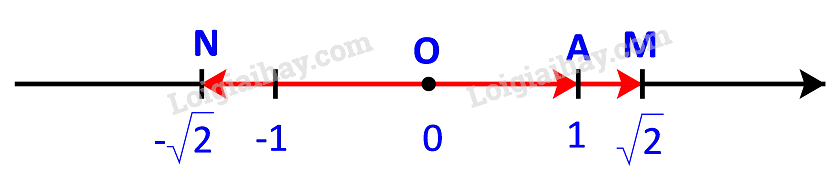
Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số \(0;\;1;\;\sqrt 2 ;\; - \sqrt 2 \). Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) với vecto \(\overrightarrow a = \overrightarrow {OA} \). Viết đẳng thức thể hiện mối quan hệ giữa hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \).
\(1\;\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau hay không?
Cho vecto \(\overrightarrow {AB} = \overrightarrow a \). Hãy xác định điểm C sao cho \(\overrightarrow {BC} = \overrightarrow a \)
a) Tìm mối quan hệ giữa \(\overrightarrow {AB} \) và \(\overrightarrow a + \overrightarrow a \)
b) Vecto \(\overrightarrow a + \overrightarrow a \) có mối quan hệ như thế nào về hướng và độ dài đối với vecto \(\overrightarrow a \)
Luyện tập – vận dụng 1 trang 89 Sách giáo khoa Toán 10 – Cánh Diều
Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.
Tìm các số a, b biết: \(\overrightarrow {AG} = a.\overrightarrow {AM} ;\overrightarrow {GN} = b.\overrightarrow {GB} \)
Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} = 2\overrightarrow {PQ} \)
B. \(\overrightarrow {MN} = 2\overrightarrow {NP} \)
C. \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
D. \(\overrightarrow {MQ} = - 2\overrightarrow {NP} \)
Cho đoạn thẳng AB = 6 cm.
a) Xác định điểm C thỏa mãn \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
b) Xác định điểm D thỏa mãn \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} \)
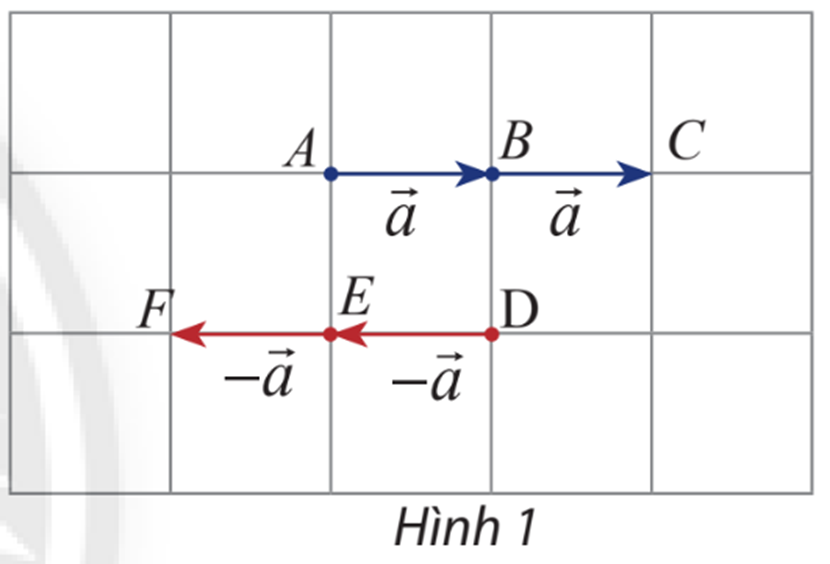
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)







Danh sách bình luận