Bảng thống kê dưới đây cho biết nhiệt độ trong một ngày mùa đông của một vùng xứ lạnh:
![]()
a) Đọc và viết nhiệt độ lúc 2 giờ, 10 giờ, 18 giờ, 22 giờ.
b) Xác định tính đúng, sai của các phát biểu sau:
- Lúc 6 giờ nhiệt độ là \(-10^oC\);
- Lúc 14 giờ nhiệt độ là \(-3^oC\).
a)
Viết:
- Nhiệt độ lúc 2 giờ, 10 giờ, 18 giờ, 22 giờ lần lượt là số ở bên dưới các giờ đó.
Đọc từ trái qua phải:
- Có dấu “ – ” thì đọc là âm.
- Đọc tiếp số đằng sau dấu trừ.
- \(^\circ C\) đọc là độ C.
Viết:
- Âm viết là “ – ”
- Viết số đằng sau dấu “ – ”.
- Viết thêm đơn vị \(^\circ C\)
a) +) Nhiệt độ lúc 2 giờ:
- Đọc là: âm tám độ C.
- Viết là: \( - 8^\circ C\).
+) Nhiệt độ lúc 10 giờ:
- Đọc là: âm năm độ C
- Viết là: \( - 5^\circ C\).
+) Nhiệt độ lúc 18 giờ:
- Đọc là: không độ C
- Viết là: \(0^\circ C\).
+) Nhiệt độ lúc 22 giờ:
- Đọc là: âm ba độ C
- Viết là: \( - 3^\circ C\).
b) Lúc 6 giờ nhiệt độ là \( - 10^\circ C\)=> Đúng
Lúc 14 giờ nhiệt độ là \( - 3^\circ C\)=> Sai vì lúc này nhiệt độ là \(2^\circ C\).
Loigaihay.com

Các bài tập cùng chuyên đề
Mỗi nhiệt kế dưới đây chỉ bao nhiêu độ C?

Liệt kê các phần tử của mỗi tập hợp sau:
a) \(A = {\rm{\{ x}} \in \mathbb{Z}\,{\rm{|}}\,{\rm{ - 2}} \le {\rm{x}}\,{\rm{ < }}\,{\rm{4\} ;}}\)
b) \(B = {\rm{\{ x}} \in \mathbb{Z}\,{\rm{|}}\,{\rm{ - 2}}\,{\rm{ < }}\,{\rm{x}}\, \le {\rm{4\} }}\).
Liệt kê các phần tử của tập hợp sau rồi tính tổng của chúng
a) S = \({\rm{\{ }}x \in \mathbb{Z}| - 5 < x \le 5\} ;\)
b) T = \({\rm{\{ }}x \in \mathbb{Z}| - 7 \le x < 1\} .\)
Dùng số nguyên âm hoặc số nguyên dương để diễn tả các thông tin sau:
a) Khi đọc sách, bạn Quang thường đưa trang sách lại quá gần mắt. Bạn ấy đã phải mang kính cận 1 dioptre.
b) Ông của bạn Quang đã già nên phải dùng kính lão 2 dioptre để đọc sách báo.
Số -3 đọc là "âm 3". Tương tự, hãy đọc các số âm mà em thấy trên bản đồ thời tiết (h.3. 1) và trên chiếc nhiệt kế (h.3.2).

Bằng cách sử dụng dấu "-", hãy viết các số âm được nói đến trong hình 3.3.

a) Viết ba số nguyên dương và ba số nguyên âm;
b) Đọc các số mà em đã viết.
Dùng số nguyên thích hợp để diễn tả các tính huống sau:
a) Thưởng 5 điểm trong một cuộc thi đấu.
b) Bớt 2 điểm vì phạm luật.
c) Tăng 1 bậc lương do làm việc hiệu quả.
d) Hạ 2 bậc xếp loại do thi đấu kém.
Các phát biểu sau đúng hay sai?
a) \(9 \in \mathbb{N}\) b) \( - 6 \in \mathbb{N}\)
c) \( - 3 \in \mathbb{Z}\) d) \(0 \in \mathbb{Z}\)
e) \(5 \in \mathbb{Z}\) g) \(20 \in \mathbb{N}\)
Hãy liệt kê các phần tử của mỗi tập hợp sau:
a) \(A = \left\{ {a \in \mathbb{Z}| - 4 < a < - 1} \right\}\)
b) \(B = \left\{ {b \in \mathbb{Z}| - 2 < b < 3} \right\}\)
c) \(C = \left\{ {c \in \mathbb{Z}| - 3 < c < 0} \right\}\)
d) \(A = \left\{ {d \in \mathbb{Z}| - 1 < d < 6} \right\}\)
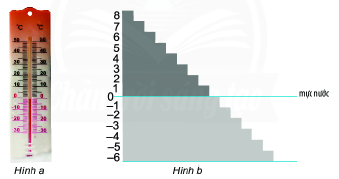
a) Quan sát nhiệt kế trong Hình a.
- Hãy đọc các số chỉ nhiệt độ (độ C) ở trên mực số 0.
- Hãy cho biết các số chỉ nhiệt độ dưới mực số 0 có mang dấu gì.
b) Quan sát Hình b, em thấy các bậc thang có độ cao mang dấu trừ thì nằm ở trên hay ở dưới mực nước?
c) Hãy cho biết những phép tính nào sau đây không thực hiện được trên tập số tự nhiên.
\(4 + 3\); \(4 - 3\);
\(2 + 5\); \(2 - 5\).
Hãy đọc các số nguyên âm chỉ nhiệt độ dưới \(0^\circ C\) sau đây: \( - 4^\circ C, - 10^\circ C, - 23^\circ C\).
Ta đã biết \(\mathbb{N} = \left\{ {0;1;2;3;...} \right\}\) là tập hợp số tự nhiên. Còn \(\mathbb{Z} = \left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\) là tập hợp bao gồm các loại số nào?
a) Đọc các số sau: -9; -18.
b) Viết các số sau: trừ hai mươi ba; âm ba trăm bốn mươi chín.
Viết các số nguyên biểu thị độ cao so với mực nước biển trong các tình huống sau:
a) Máy bay ở độ cao 10 000 m;
b) Mực nước biển;
c) Tàu ngầm chạy dưới mực nước biển 100 m.
a) Đọc số: -54
b) Âm chín mươi.
Viết số nguyên âm biểu thị độ cao của tàu ngầm so với mực nước biển, biết tàu ngầm đang ở vị trí dưới mực nước biển 20 m.
Diễn đạt lại thông tin sau mà không dùng số âm: “Độ cao trung bình của thềm lục địa Việt Nam là – 65 m”.
Số nguyên nào thích hợp để mô tả mỗi tình huống sau:
a) Thưởng 10 điểm trong một cuộc thi đấu
b) Bớt 4 điểm vi phạm luật
c) Nhiệt độ ngăn đá tủ là 5 độ dưới \({0^o}C\).
d) Rút 3 000 000 đồng từ thẻ ATM
e) Đỉnh núi Fansipan (Phan-xi-păng) cao 3143m so với mực nước biển.
Điểm cách \(-1\) ba đơn vị theo chiều âm là:
-
A.
\(3\)
-
B.
\(-3\)
-
C.
\(-4\)
-
D.
\(4\)
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
-
A.
3
-
B.
5
-
C.
2
-
D.
4
Cho \(C = \left\{ { - 3;\, - 2;\,0;\,1;\,6;\,10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
-
A.
\(D = \left\{ { - 3;\, - 2;\,0} \right\}\)
-
B.
\(D = \left\{ { - 3;\, - 2} \right\}\)
-
C.
\(D = \left\{ { 0;\, 1;\, 6;\, 10} \right\}\)
-
D.
\(D = \left\{ { - 3;\, - 2;\, 6;\, 10;\, 1} \right\}\)
Những điểm cách điểm \(0\) ba đơn vị là:
-
A.
\(3\) và \(-3\)
-
B.
\(2\) và \(-2\)
-
C.
\(2\) và \(-3\)
-
D.
\(3\) và \(-2\)
Những điểm cách điểm \(3\) năm đơn vị là:
-
A.
\(7\) và \(-1\)
-
B.
\(6\) và \(-2\)
-
C.
\(2\) và \(-2\)
-
D.
\(8\) và \(-2\)
Nếu \(-30 \ m\) biểu diễn độ sâu là \(30 \ m\) dưới mực nước biển thì \(+20 \ m\) biểu diễn độ cao là:
-
A.
\(-20 \ m\) dưới mực nước biển
-
B.
\(20 \ m\) dưới mực nước biển
-
C.
\(-20 \ m\) trên mực nước biển
-
D.
\(20 \ m\) trên mực nước biển
Điểm \(-2\) cách điểm \(3\) bao nhiêu đơn vị?
-
A.
\(5\)
-
B.
\(2\)
-
C.
\(1\)
-
D.
\(8\)
Chọn câu sai
-
A.
\(-5 < -2\);
-
B.
\(0 < 4\);
-
C.
\(0 > -1\);
-
D.
\(-5 < -6\)
Số liền trước của số \(-19\) là số
-
A.
\(20\)
-
B.
\(-17\)
-
C.
\(-18\)
-
D.
\(-20\)
Nhiệt kế chỉ bao nhiêu độ trong hình dưới đây?
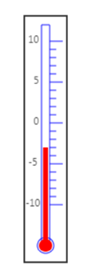
-
A.
\(8^{o}C\);
-
B.
\(-3^{o}C\);
-
C.
\(3^{o}C\);
-
D.
\(6^{o}C\);
Tập hợp nào dưới đây gồm các số nguyên âm
-
A.
\(\left\{ { - 3;\, - 2;\, 1} \right\}\);
-
B.
\(\left\{ { - 9;\, - 2;\, - 1} \right\}\);
-
C.
\(\left\{ { - 6;\, 1;\, 4} \right\}\);
-
D.
\(\left\{ { 1;\, 4;\, 8} \right\}\).







Danh sách bình luận