Cho hàm số \(y = 2{x^2} + x + m\). Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}};{y_S} = f(\frac{{ - b}}{{2a}})\)
\(a = 2 > 0\) nên ta có bảng biến thiên sau:
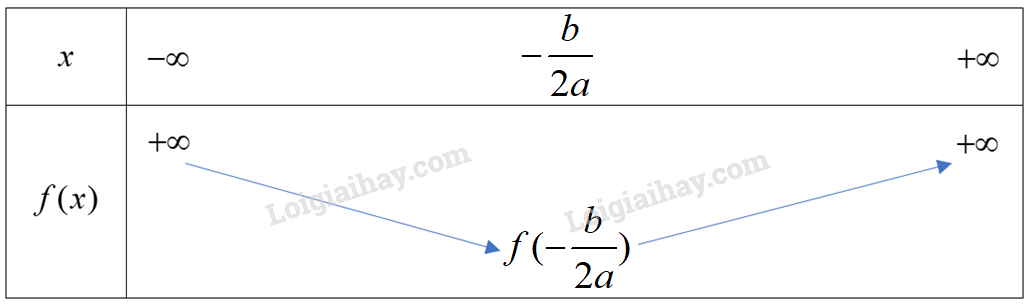
Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{b}{{2a}})\) tại \(x = - \frac{b}{{2a}}.\)
=> Tìm m để \(f( - \frac{b}{{2a}}) = 5\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} = - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}\)
Ta có: \(a = 2 > 0\), hàm số có bảng biến thiên dạng:
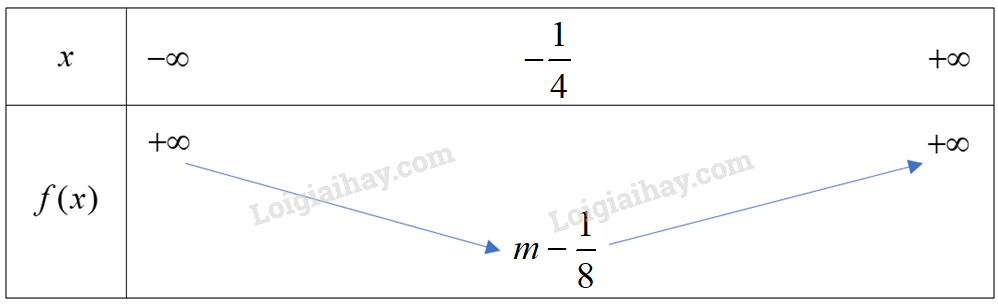
Hàm số đạt giá trị nhỏ nhất bằng \(m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.\)
Vậy \(m = \frac{{41}}{8}\) thì hàm số đạt giá trị nhỏ nhất bằng 5.

Các bài tập cùng chuyên đề
Lập bảng biến thiên của mỗi hàm số sau:
a) \(y = {x^2} - 3x + 4\)
b) \(y = - 2{x^2} + 5\)
a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
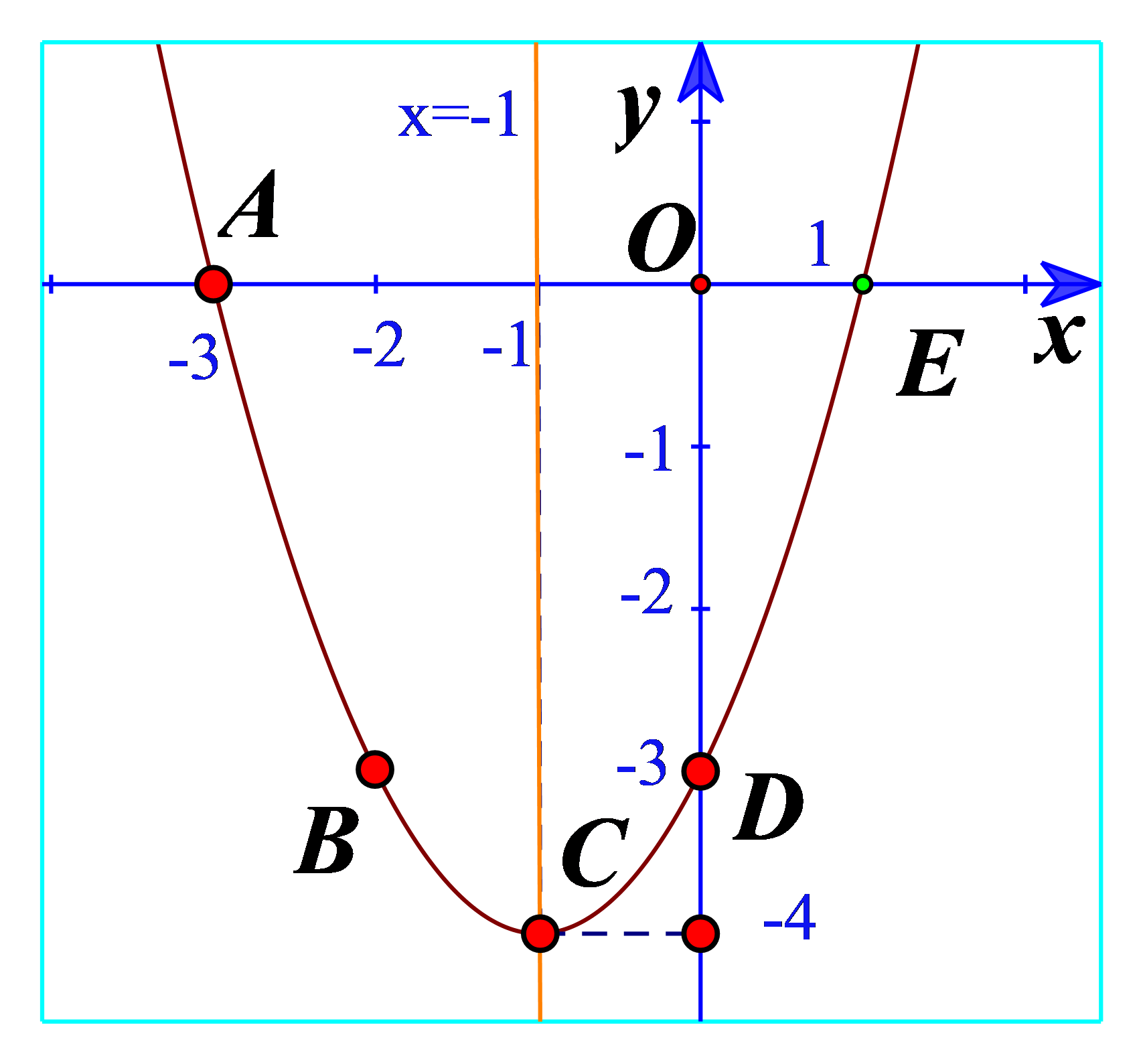
b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
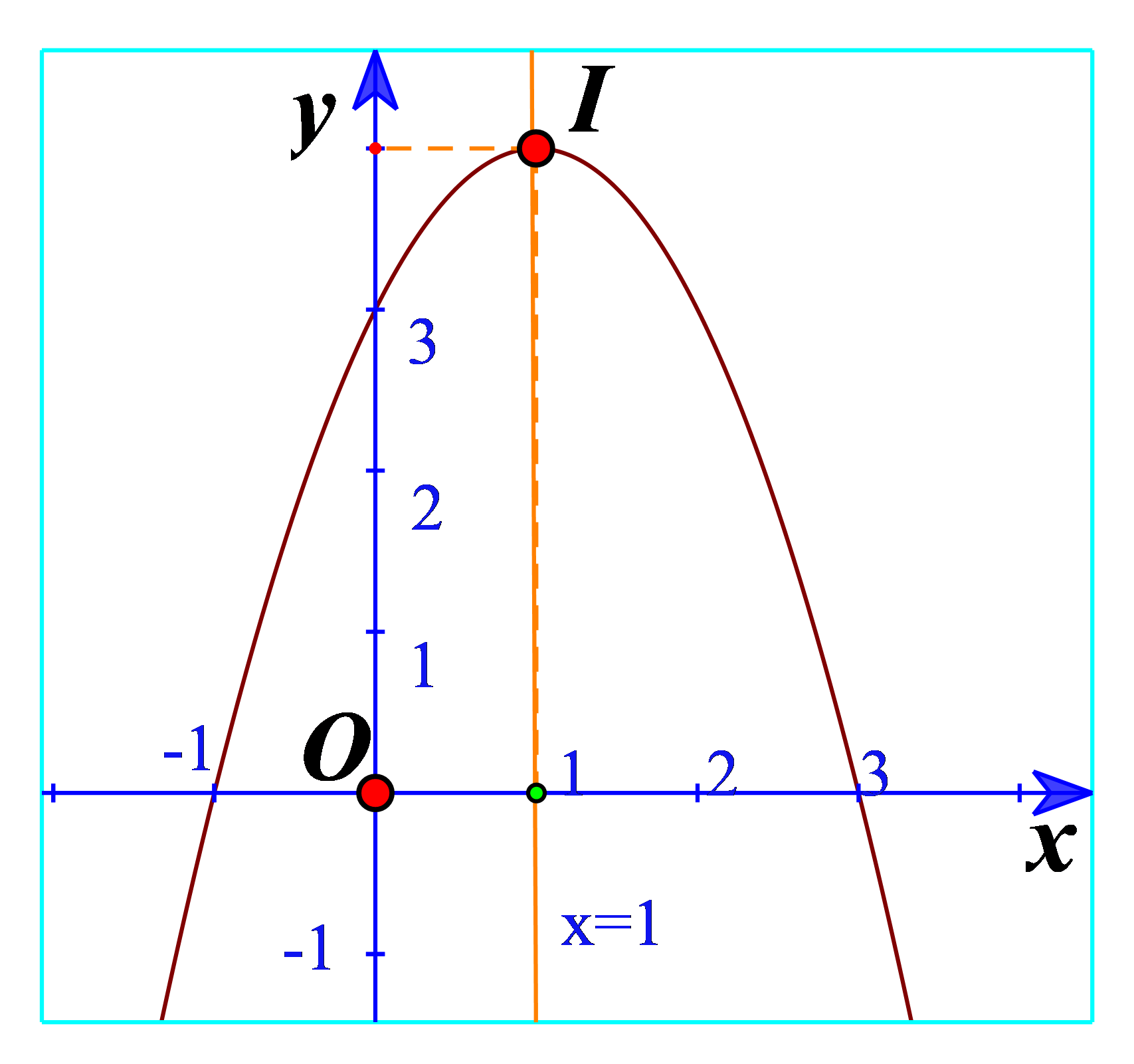
Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:
a) \(y = 5{x^2} + 4x - 1\)
b) \(y = - 2{x^2} + 8x + 6\)
Tìm khoảng đồng biến, khoảng nghịch biến của hàm số \(y = 2{x^2} - 6x + 11.\) Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.

Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Biết rằng hàm số \(y = 2{x^2}{\rm{ + }}mx + n\) giảm trên khoảng \(\left( { - \infty ;1} \right),\)tăng trên khoảng \(\left( {1; + \infty } \right)\) và có tập giá trị là \([9; + \infty )\). Xác định giá trị của m và n.
Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:
a) \(y = 4{x^2} + 6x - 5\)
b) \(y = - 3{x^2} + 10x - 4\)
Tìm khoảng biến thiên và tập giá trị của các hàm số sau:
a) \(y = f\left( x \right) = - 2{x^2} - 4x + 7\)
b) \(y = f\left( x \right) = {x^2} - 6x + 1\)
Hàm số \(y = f\left( x \right) = - \left( {x + 2} \right)\left( {x - 4} \right)\) đồng biến trên khoảng
A. \(\left( { - \infty ; - 1} \right)\)
B. \(\left( {1; + \infty } \right)\)
C. \(\left( { - \infty ;1} \right)\)
D. \(\left( { - 1; + \infty } \right)\)
Từ các parabol đã vẽ ở Bài tập 6.7, hãy cho biết khoảng đồng biến và khoảng nghịch biến của mõi hàm số bậc hai tương ứng.
Hàm số \(y = {x^2} - 5x + 4\)
A. Đồng biến trên khoảng \((1; + \infty ).\)
B. Đồng biến trên khoảng \(( - \infty ;4).\)
C. Nghịch biến trên khoảng \(( - \infty ;1).\)
D. Nghịch biến trên khoảng \((1;4).\)
Cho hàm số \(y = {x^2} - 2x + 3\). Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên \(\left( { - \infty ;2} \right)\)
B. Hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\)
C. Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\)
D. Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\)







Danh sách bình luận