Cho các định lí:
P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.
Q: “Nếu \(a < b\) thì \(a + c < b + c\)” (\(a,b,c \in \mathbb{R}\)).
a) Chỉ ra giả thiết và kết luận của mỗi định lí.
b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.
c) Mệnh đề đảo của mỗi định lí đó có là định lí không?
+) Khi mệnh đề \(R \Rightarrow T\) là định lí, ta nói:
R là giả thiết, T là kết luận
R là điều kiện đủ để có T
T là điều kiện cần để có R
+) Mệnh đề đảo của mệnh đề \(R \Rightarrow T\) là mệnh đề \(T \Rightarrow R\).
a)
Mệnh đề P có dạng \(R \Rightarrow T\)với R: “Hai tam giác bằng nhau” và T: “Diện tích của hai tam giác bằng nhau”
Giả thiết là mệnh đề R: “Hai tam giác bằng nhau”
Kết luận là mệnh đề T: “Diện tích của hai tam giác bằng nhau”
Mệnh đề Q có dạng \(A \Rightarrow B\)với A: “\(a < b\)” và B: “\(a + c < b + c\)”
Giả thiết là mệnh đề A: “\(a < b\)”
Kết luận là mệnh đề B: “\(a + c < b + c\)”
b)
+) Mệnh đề P có thể phát biểu lại như sau:
Hai tam giác bằng nhau là điều kiện đủ để có diện tích của chúng bằng nhau.
Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác bằng nhau.
+) Mệnh đề Q có thể phát biểu lại như sau:
\(a < b\) là điều kiện đủ để có \(a + c < b + c\).
\(a + c < b + c\)là điều kiện cần để có \(a < b\).
c)
Mệnh đề đảo của mệnh đề P có dạng \(T \Rightarrow R\), phát biểu là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.
Mệnh đề này sai nên không là định lí.
Chẳng hạn: Tam giác ABC và tam giác DEF, có diện tích bằng nhau nhưng hai tam giác không bằng nhau.
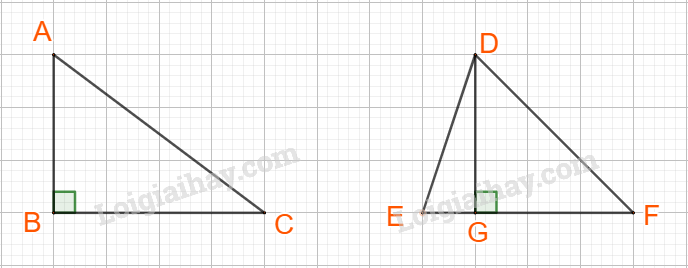
Mệnh đề đảo của mệnh đề Q có dạng \(B \Rightarrow A\), phát biểu là: “Nếu \(a + c < b + c\)thì \(a < b\)”.
Mệnh đề này đúng nên nó cũng là định lí.
Các bài tập cùng chuyên đề
Với hai số thực a và b, xét mệnh đề P: “\({a^2} < {b^2}\)” và Q: “\(0 < a < b\)”
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\);
b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a.
c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b.
Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.
Q: “\(\exists \;n \in \mathbb{N},n\) chia hết cho \(n + 1\)”
Trong các khẳng định sau, khẳng định nào là mệnh đề, khẳng định nào là mệnh đề chứa biến
a) \(3 + 2 > 5\)
b) \(1 - 2x = 0\)
c) \(x - y = 2\)
d) \(1 - \sqrt 2 < 0\)
Cho hai mệnh đề sau:
P: “Tứ giác \(ABCD\) là hình bình hành”.
Q: “Tứ giác \(ABCD\) có \(AB\)//\(CD\) và \(AB = CD\)”.
Hãy phát biểu mệnh đề \(P \Rightarrow Q\) và mệnh đề đảo của mệnh đề đó.
Cho mệnh đề kéo theo có dạng \(P \Rightarrow Q\): “Vì 120 chia hết cho 6 nên 120 chia hết cho 9”.
a) Mệnh đề trên đúng hay sai?
b) Phát biểu mệnh đề đảo của mệnh đề trên và xét tính đúng sai của mệnh đề đảo đó.
Cho mệnh đề kéo theo có dạng \(P \Rightarrow Q\): “Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”.
a) Mệnh đề trên đúng hay sai?
b) Phát biểu mệnh đề đảo của mệnh đề trên và xét tính đúngg sai của mệnh đề đảo đó.
Cho tam giác ABC với đường trungg tuyến AM. Xét các mệnh đề:
P: “Tam giác ABC vuông tại A”.
Q: “Độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC”.
a) Phát biểu mệnh đề \(P \Rightarrow Q,Q \Rightarrow P\) và xác định tính đúng sai của mỗi mệnh đề đó.
b) Nếu cả hai mệnh đề trong ý a) là đúng, hãy phát biểu mệnh đề tương đương.
Cho phương trình \(a{x^2} + bx + c = 0\).
a) Xét mệnh đề “Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\) có một nghiệm bằng 1”. Mệnh đề này đúng hay sai?
b) Phát biểu mệnh đề đảo của mệnh đề trên. Mệnh đề đảo đúng hay sai?
c) Nêu điều kiện cần vào đủ để phương trình \(a{x^2} + bx + c = 0\) có một nghiệm bằng 1.
Cho \(P(n) = {n^2} - 6n + 10\) với n là số tự nhiên.
Cho hai mệnh đề sau:
P: “Hình bình hành có một góc vuông là hình chữ nhật”.
Q: “Số 7 là hợp số”.
Xét mệnh đề chứa biến P(x): “\(x \in \mathbb{N},{x^2} - 2x = 0\)”. Có bao nhiêu giá trị của biến để được mệnh đề đúng?
Cho P: “3x + 6 = 0”.
Có bao nhiêu giá trị nguyên của m để mệnh đề chứa biến “\( - {x^2} + 2mx - 4 < 0\)” là mệnh đề đúng?
Cho các mệnh đề:
P: “Tam giác ABC là tam giác vuông tại A”
Q: “Tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
a) Hãy phát biểu các mệnh đề: \(P \Rightarrow Q,Q \Rightarrow P,P \Leftrightarrow Q,\overline P \Rightarrow \overline Q .\) Xét tính đúng sai của các mệnh đề này.
b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề \(P \Rightarrow Q\)
c) Gọi X là tập hợp các tam giác ABC vuông tại A, Y là tập hợp các tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\). Nêu mối quan hệ giữa hai tập hợp X và Y.
