Cho hàm số \(y = \frac{1}{x}\). Chứng tỏ hàm số đã cho:
a) Nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
b) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
a) Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
a) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( {0; + \infty } \right) \Rightarrow {x_1}{x_2} > 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( { - \infty ;0} \right) \Rightarrow {x_1}{x_2} > 0\)(Cùng dấu âm nên tích cũng âm)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\).
Các bài tập cùng chuyên đề
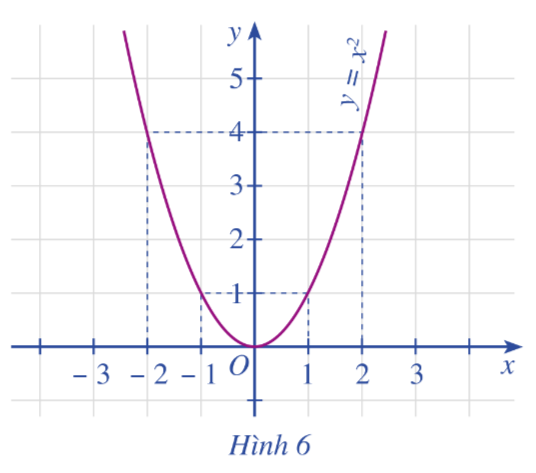
Cho đồ thị hàm số \(y = f\left( x \right) = {x^2}\) như Hình 6.
a) So sánh \(f\left( { - 2} \right),f\left( { - 1} \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1.
b) So sánh \(f\left( 1 \right),f\left( 2 \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
Chứng tỏ hàm số \(y = 6{x^2}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Cho hàm số \(f\left( x \right) = x + 1\).
a) So sánh \(f\left( 1 \right)\) và \(f\left( 2 \right)\).
b) Chứng minh rằng nếu \({x_1},{x_2} \in \mathbb{R}\) sao cho \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
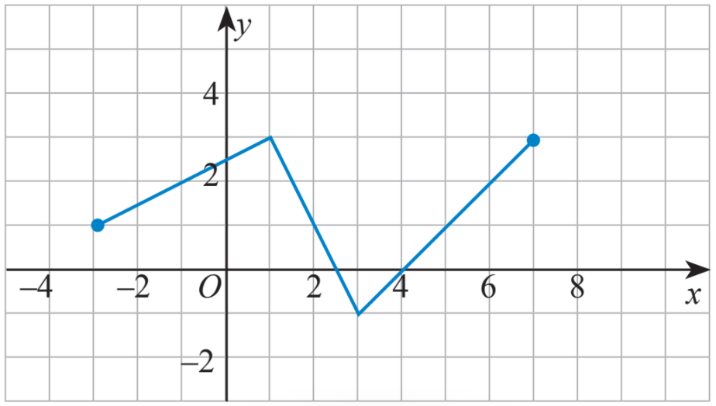
Cho hàm số \(y = f\left( x \right)\) có đồ thị như Hình 9. Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\).
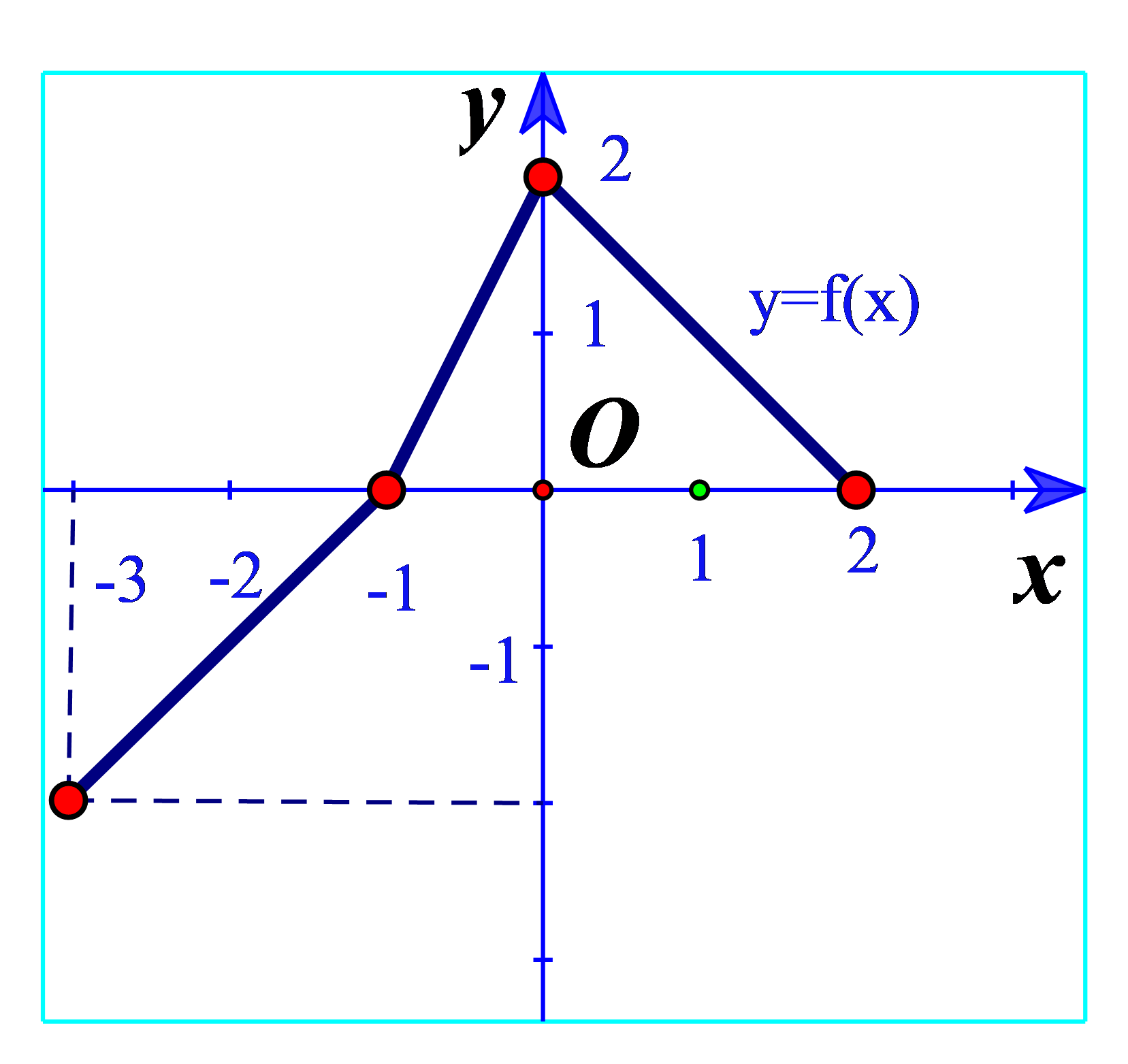
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
Quan sát đồ thị hàm số \(y = f(x) = {x^2}\) rồi so sánh \(f({x_1})\) và \(f({x_2})\) (với \({x_1} < {x_2}\)) trong từng trường hợp sau:
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a) \(f(x) = - 5x + 2\)
b) \(f(x) = - {x^2}\)
Cho bảng biến thiên hàm số \(y = f\left( x \right)\) như sau:
a) Tìm khoảng đồng biến, ngịch biến của hàm số \(y = f\left( x \right)\).
b) So sánh \(f\left( { - 2021} \right)\) và \(f\left( { - 1} \right)\); \(f\left( {\sqrt 3 } \right)\) và \(f\left( 2 \right)\).
Cho hàm số \(y = \frac{{ - 2}}{x}\). Chứng tỏ hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Cho hàm số \(f\left( x \right) = 2{x^2} + 8x + 8\). Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng \(\left( { - 4; + \infty } \right)\), nghịch biến trên khoảng \(\left( { - \infty ; - 4} \right)\)
B. Hàm số đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\), nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\)
C. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\), nghịch biến trên khoảng \(\left( { - 2; + \infty } \right)\)
D. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 4} \right)\), nghịch biến trên khoảng \(\left( { - 4; + \infty } \right)\)
Tìm khoảng đồng biến và nghịch biến của các hàm số sau:
a) \(f\left( x \right) = \frac{1}{{ - x - 5}}\)
b) \(f\left( x \right) = \left| {3{\rm{x}} - 1} \right|\)
Tìm khoảng đồng biến, nghịch biến của các hàm số sau:
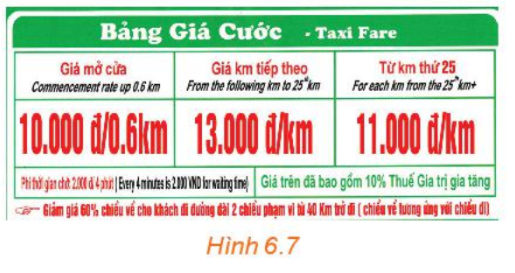
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Vẽ đồ thị của hàm số \(y = 3x + 1\) và \(y = - 2{x^2}\). Hãy cho biết:
a) Hàm số \(y = 3x + 1\) đồng biến hay nghịch biến trên \(\mathbb{R}\).
b) Hàm số \(y = - 2{x^2}\)đồng biến hay nghịch biến trên \(( - \infty ;0)\) và \((0; + \infty )\).
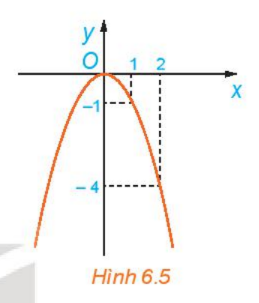
Quan sát đồ thị của hàm số \(y = f(x) = - {x^2}\) trên \(\mathbb{R}\)(H.6.5).
a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \(( - \infty ;0)\)?
b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \((0; + \infty )\)?
Cho hàm số \(y = - x + 1\) và \(y = x\). Tính giá trị y theo giá trị x để hoàn thành bảng sau:
Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số \(y = - x + 1\) và \(y = x\) tăng hay giảm?
Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.
a) \(y = - 2x + 1\)
b)\(y = - \frac{1}{2}{x^2}\)
Với những giá trị nào của m thì hàm số \(f(x) = (m + 1)x + 2\) đồng biến trên \(\mathbb{R}\)?
A. m > -1
B. m = 1
C. m < 0
D. m = 0
