Hãy chỉ ra trên Hình 4.26 hai vecto \(3\left( {\overrightarrow u + \overrightarrow v } \right)\) và \(3\overrightarrow u + 3\overrightarrow v \). Từ đó, nêu mối quan hệ giữa \(3\left( {\overrightarrow u + \overrightarrow v } \right)\) và \(3\overrightarrow u + 3\overrightarrow v \)
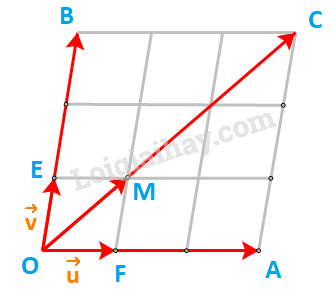
Kí hiệu O, E, F là các điểm như trên hình vẽ.
Dễ thấy: tứ giác OEMF là hình bình hành nên \(\overrightarrow {OE} + \overrightarrow {OF} = \overrightarrow {OM} \) hay \(\overrightarrow v + \overrightarrow u = \overrightarrow {OM} \)
Và \(\overrightarrow {OC} = 3.\overrightarrow {OM} \Rightarrow 3\left( {\overrightarrow v + \overrightarrow u } \right) = 3.\overrightarrow {OM} = \overrightarrow {OC} \)
Mặt khác: \(\overrightarrow {OA} = 3.\overrightarrow {OF} = 3\;\overrightarrow u ;\;\overrightarrow {OB} = 3.\overrightarrow {OE} = 3\;\overrightarrow v \)
Và \(\overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {OC} \) hay \(3\;\overrightarrow v + 3\;\overrightarrow u = \overrightarrow {OC} \)
\( \Rightarrow 3\left( {\overrightarrow v + \overrightarrow u } \right) = 3\;\overrightarrow v + 3\;\overrightarrow u \)

Các bài tập cùng chuyên đề
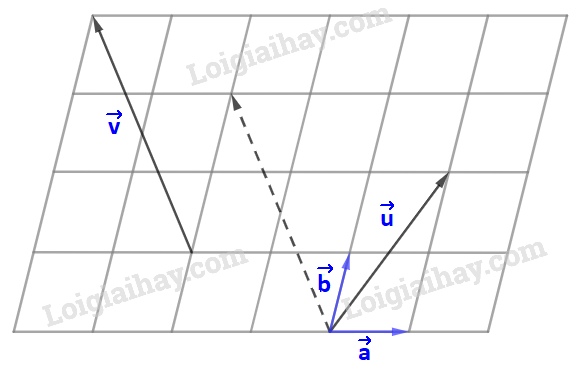
Trong hình 4.27, hãy biểu thị mỗi vecto \(\overrightarrow u ,\;\overrightarrow v \) theo hai vecto \(\overrightarrow a ,\;\overrightarrow b \), tức là tìm các số \(x,y,z,t\) để \(\overrightarrow u = x\overrightarrow a + y\overrightarrow b ,\;\overrightarrow v = t\overrightarrow a + z\overrightarrow b .\).
Với \(\overrightarrow u \ne \overrightarrow 0 \) và hai số thực k, t, những khẳng định nào sau đây là đúng?
a) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) có cùng độ dài bằng \(\left| {kt} \right|.\left| {\overrightarrow u } \right|\)
b) Nếu \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
c) Nếu \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
d) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) bằng nhau.
Luyện tập – vận dụng 2 trang 89 Sách giáo khoa Toán 10 – Cánh Diều
Cho ba điểm A, B, C. Chứng minh \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right) = \overrightarrow {AB} \)
Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lý/giờ. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của tàu B theo vectơ vận tốc \(\overrightarrow a \) của tòa A.

Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
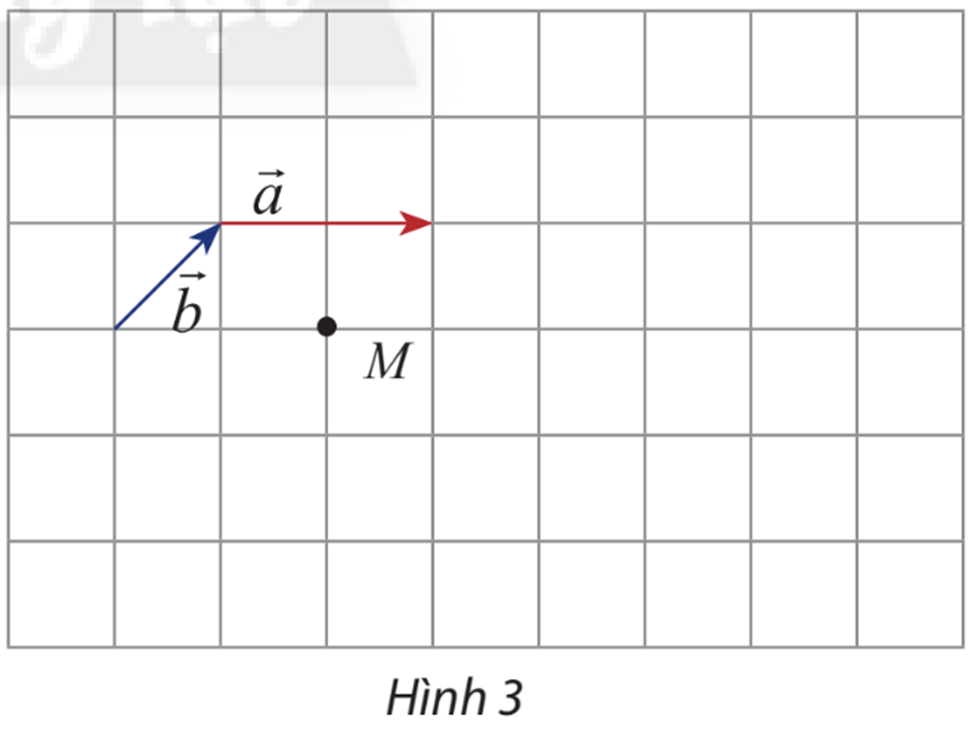
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).
Cho ba điểm A, B, M như hình vẽ:

-
A.
\(\overrightarrow {MB} = 3\overrightarrow {MA} \)
-
B.
\(\overrightarrow {MB} = \frac{1}{3}\overrightarrow {AB} \)
-
C.
\(\overrightarrow {AB} = 4\overrightarrow {MA} \)
-
D.
\(\overrightarrow {MB} = - 3\overrightarrow {MA} \)






