Cho tam giác ABC có AB = 5, AC = 8 và \(\widehat A = {45^o}\). Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Bước 1: Tính cạnh BC (tương ứng là a) theo công thức \({a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\)
Bước 2: Tính cos B (theo công thức \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\)) từ đó suy ra góc B.
Bước 3: Tính góc C.
Áp dụng định lí cosin trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\end{array}\)
(trong đó: AB = c, BC = a và AC = b)
Ta được: \(B{C^2} = {a^2} = {8^2} + {5^2} - 2.8.5.\cos {45^o} = 89 - 40\sqrt 2 \)\( \Rightarrow BC \approx 5,7\)
Từ (2) suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\);
Mà: a = BC =5,7; b =AC = 8; c =AB =5.
\( \Rightarrow \cos B \approx \frac{{ - 217}}{{1900}} \Rightarrow \widehat B \approx {97^o} \Rightarrow \widehat C \approx {38^o}\)
Vậy tam giác ABC có BC = 5,7, \(\widehat B = {97^o},\widehat C = {38^o}\)
Các bài tập cùng chuyên đề
Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ 1b.
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí cosin tại đỉnh A đối với tam giác đó.
Từ định lí cosin hãy viết các công thức tính cos A, cos B, cos C theo độ dài các cạnh a, b, c của tam giác ABC.
Định lí Pythagore có phải là một trường hợp đặc biệt của định lí cosin hay không?
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng đông nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1 cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilomet (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng định lí Pythagore (Pi-ta-go) để tính chính xác các số đo trong câu b hay không?
Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a) \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) \(M{A^2} + M{B^2} - A{B^2} = 2.MA.MB.\cos \widehat {AMB}\) và \(M{A^2} + M{C^2} - A{C^2} = 2.MA.MC.\cos \widehat {AMC}\)
c) \(M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\) (công thức đường trung tuyến).
Cho tam giác ABC. Chứng minh rằng:
a) Nếu góc A nhọn thì \({b^2} + {c^2} > {a^2}\)
b) Nếu góc A tù thì \({b^2} + {c^2} < {a^2}\)
c) Nếu góc A vuông thì \({b^2} + {c^2} = {a^2}\)
Cho tam giác ABC có AB = 5, AC = 6, BC =7. Tính cosA.
Cho \(\alpha \) là góc vuông. Chứng minh \({a^2} = {b^2} + {c^2} - 2bc.\cos \alpha \)
Không dùng thước đo góc, làm thế nào để biết số đo góc đó.
Ban Hoài vẽ góc xOy và đó bạn Đông làm thế nào có thể biết được số đo của góc này khi không có thước đo góc. Bạn Đông làm như sau:
- Chọn các điểm A, B lần lượt thuộc các tia Ox và Oy sao cho OA = OB = 2 cm.
- Đo độ dài đoạn thẳng AB được AB = 3,1 cm.
Từ các dữ kiện trên bạn Đông tính được \(\cos \widehat {xOy}\) từ đó suy ra độ lớn góc xOy.
Em hãy cho biết số đo góc xOy ở Hình 69 bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị).
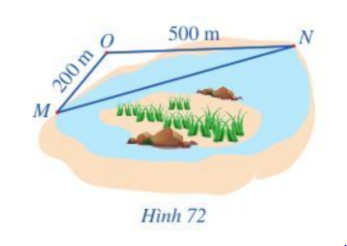
Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN, các khoảng cách OM, ON và góc MON là đo được (Hình 72). Sau khi đo, ta có OM = 200 m, ON = 500 m, \(\widehat {MON} = {135^o}.\)
Khoảng cách giữa hai vị trí M, N là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
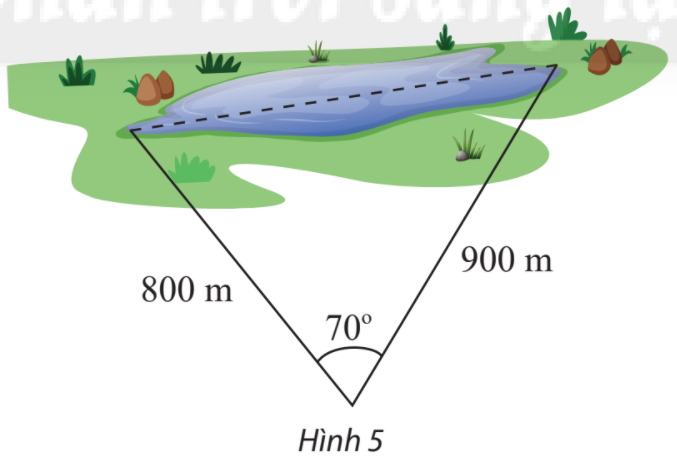
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc \({70^o}\) (Hình 5).
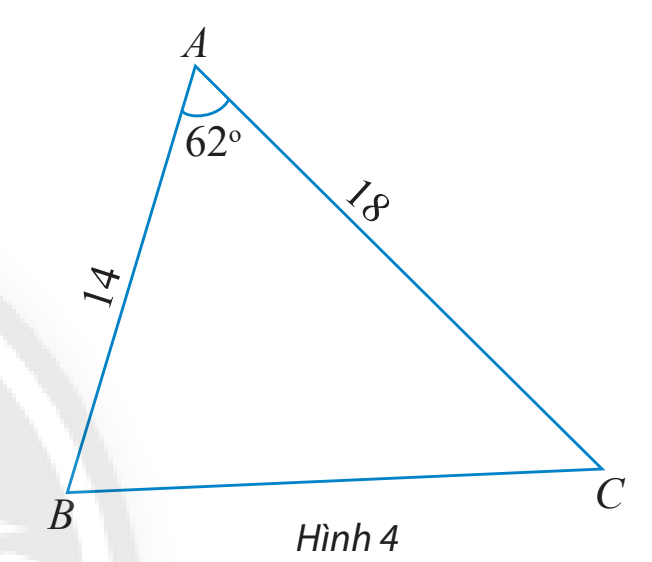
Tính các cạnh và các góc chưa biết của tam giác ABC trong hình 4.
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
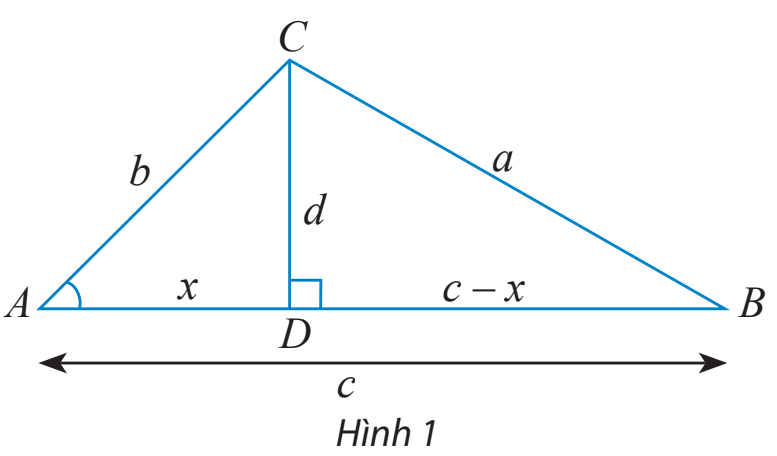
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
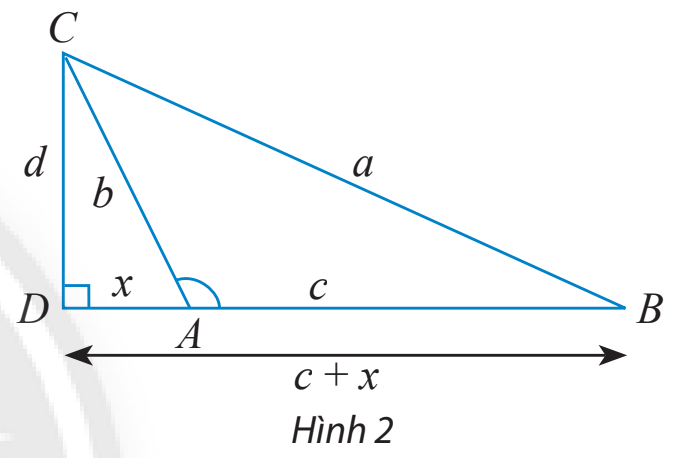
Lưu ý: Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)
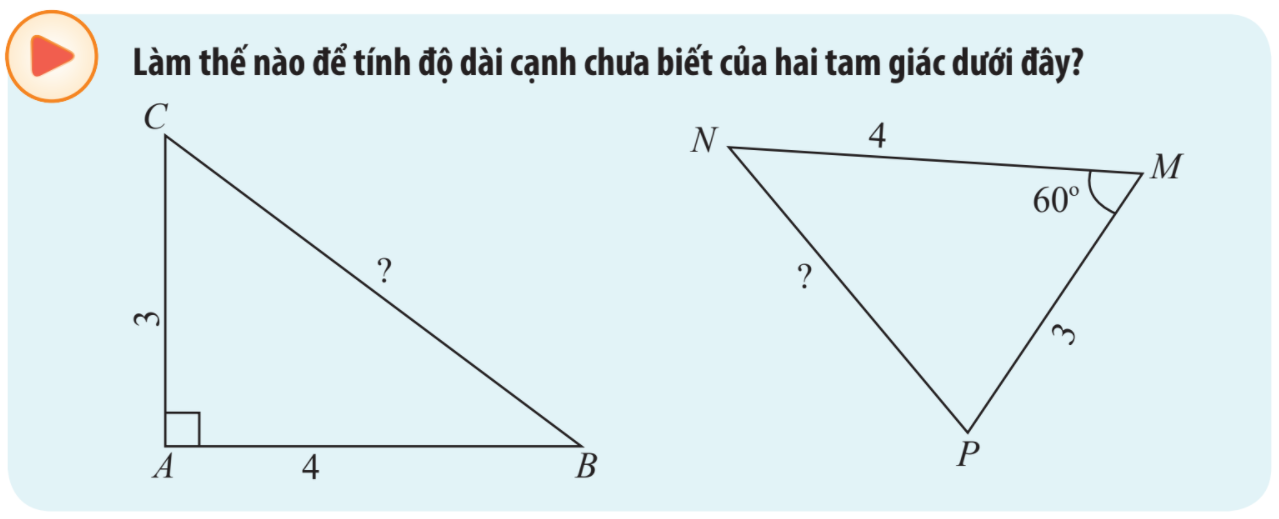
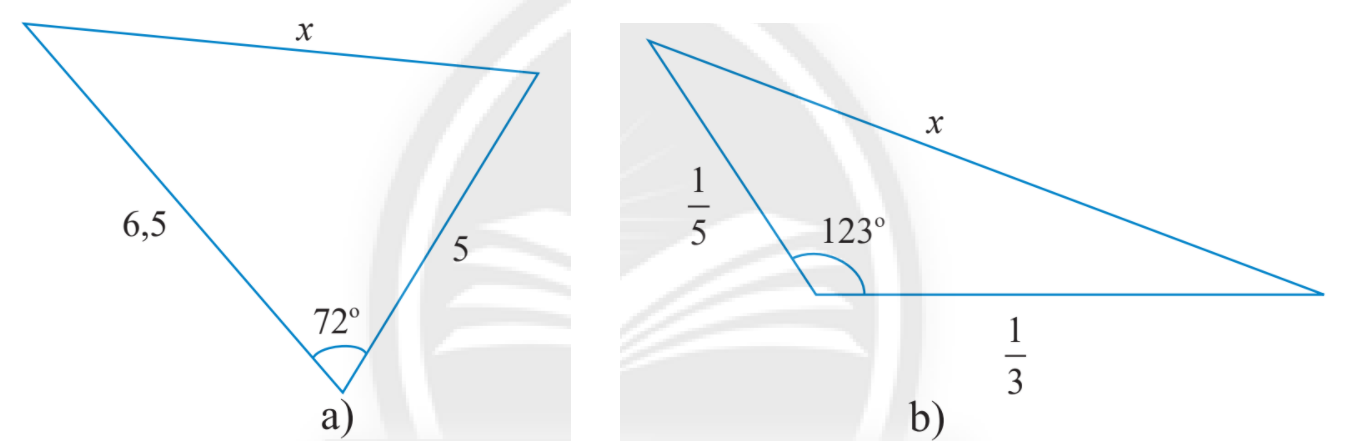
Tính độ dài cạnh x trong các tam giác sau:
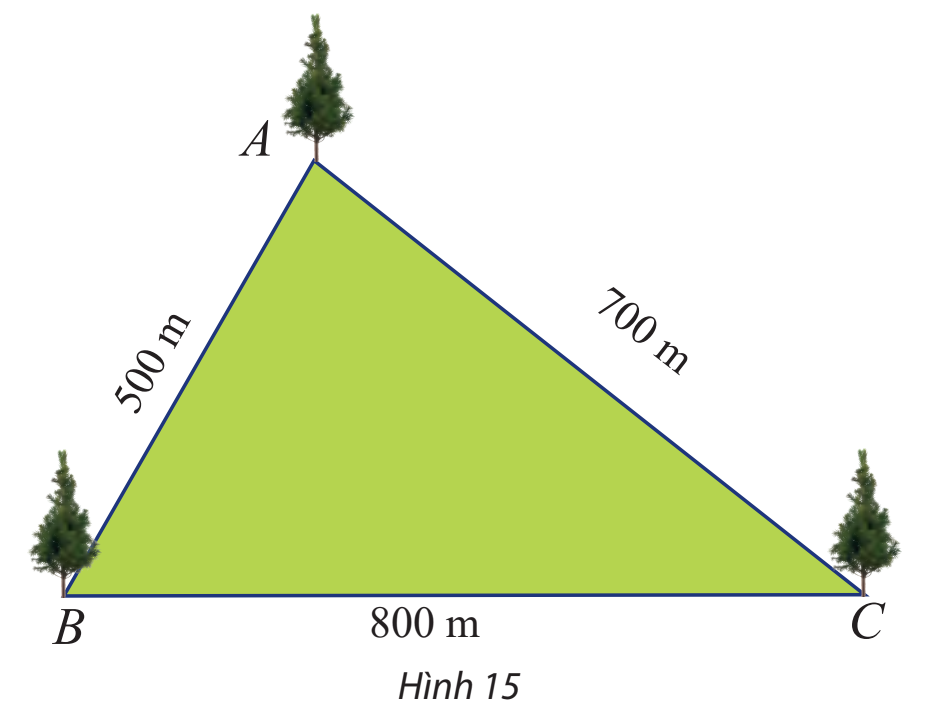
Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.
c) Lấy điểm D đối xứng với A qua C.
Tam giác ABC có BC = 1, AC = 3, C = 60°. Tính độ dài cạnh AB.
Cho tam giác ABC có cạnh AC = 14, \(\widehat B = {120^o}\), tổng hai cạnh còn lại là 16. Tính độ dài cạnh BC biết BC > AB.
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó
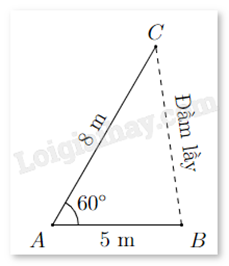
Khoảng cách từ B đến cọc tiêu C không thể đo trực tiếp vì phải qua một đầm lầy. Người ta xác định một điêm A có khoảng cách AB = 5 m và đo được \(\widehat {BAC} = {60^o}\) (xem hình vẽ). Tính khoảng cách BC biết rằng AC = 8 m.
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB và \(\widehat A = {60^o}\). Đẳng thức nào sau đây đúng?
Tam giác \(ABC\) có \(AB = \sqrt 5 ,\,\,AC = \sqrt 2 ,\,\,\widehat C = {45^ \circ }.\) Độ dài cạnh \(BC\) bằng:
A. \(3.\)
B. \(2.\)
C. \(\sqrt 3 .\)
D. \(\sqrt 2 .\)
Tính góc lớn nhất của tam giác ABC, biết các cạnh là \(a = 8,b = 12,c = 6\).
Cho tam giác ABC với \(BC = a;AC = b;AB = c\). Chứng minh rằng:
\(1 + \cos A = \frac{{\left( {a + b + c} \right)\left( { - a + b + c} \right)}}{{2bc}}\)
Cho tam giác ABC với \(BC = a;AC = b;AB = c\) và \(a = b\). Chứng minh rằng:
\({c^2} = 2{a^2}(1 - \cos C)\).
Cho tam giác ABC có \(AB = 4\) cm, \(BC = 7\) cm, \(CA = 9\). Giá trị \(\cos A\) là
A. \(\frac{2}{3}\)
B. \(\frac{1}{3}\)
C. \(\frac{4}{5}\)
D. \(\frac{8}{9}\)
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\).
