Lớp 10A có 24 bạn tham gia thi đấu bóng đá và cầu lông, trong đó có 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông. Giả sử các trận bóng đá và cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cầu lông?
Gọi x là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Sử dụng biểu đồ Ven để mô tả các tập hợp.
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
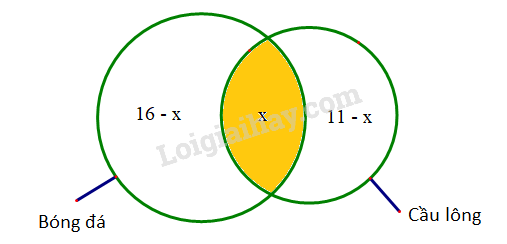
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.

Các bài tập cùng chuyên đề
Tìm phần bù của các tập hợp sau trong \(\mathbb{R}\):
a) \(\left( { - \infty ; - 2} \right)\)
b) \([ - 5; + \infty )\)
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2.
Cho hai tập hợp:
\(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\}\).
\(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} \).
Tìm \(A\,{\rm{\backslash }}\,B\) và \(B\,{\rm{\backslash }}\,A\).
Cho hai tập hợp: A = {2; 3; 5; 7; 14}, B = {3; 5; 7; 9; 11}.
Liệt kê các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.
Gọi \(\mathbb{R}\) là tập hợp các số thực, I là tập hợp các số vô tỉ. Khi đó \(I \subset \mathbb{R}\). Tìm tập hợp những số thực không phải là số vô tỉ.
Xác định các tập hợp sau đây:
a) \((1;3) \cup [ - 2;2]\)
b) \(( - \infty ;1) \cap [0;\pi ]\)
c) \([\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\)
d) \({C_\mathbb{R}}[ - 1; + \infty )\)
Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)
Xác định các tập hợp sau đây:
a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\)
b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\)
c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\)
Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.
a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.
A \ B được gọi là phần bù của B trong A khi nào?
-
A.
\(A\; \subset \;B\)
-
B.
\(\;B\; \subset \;A\)
-
C.
\(A\;\; \cap \;B\)
-
D.
\(A\;\; \cup \;B\)
Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {3;4;5;6} \right\}\). Tập hợp \(A\backslash B\) bằng:
A. \(\left\{ {0;1;2;3;4;5;6} \right\}\)
B. \(\left\{ {3;4} \right\}\)
C. \(\left\{ {0;1;2} \right\}\)
D. \(\left\{ {5;6} \right\}\)
Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}| - 2 \le x \le 5} \right\},B = \left\{ {x \in \mathbb{Z}|{x^2} - x - 6 = 0} \right\}\). Tập hợp \(A\backslash B\) bằng:
A. \(\left( { - 2;3} \right)\)
B. \(\left( { - 2;3} \right) \cup \left( {3;5} \right]\)
C. \(\left( {3;5} \right]\)
D. \(\left[ { - 2;5} \right]\backslash \left\{ 3 \right\}\)
Cho tập hợp \(A = \left[ { - 1; + \infty } \right)\). Tập hợp \({C_\mathbb{R}}A\) bằng:
A. \(\left( { - 1; + \infty } \right)\)
B. \(\left( { - \infty ; - 1} \right)\)
C. \(\left( { - \infty ; - 1} \right]\)
D. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
Cho hai tập hợp \(A = \left[ { - 4;3} \right),B = \left( { - 2; + \infty } \right).A\backslash B\) bằng:
A. \(\left[ { - 4; - 2} \right)\)
B. \(\left\{ { - 4; - 3; - 2} \right\}\)
C. \(\left[ {3; + \infty } \right)\)
D. \(\left[ { - 4; - 2} \right]\)
Cho \(U = \left\{ {3;5;{a^2}} \right\},A = \left\{ {3;a + 4} \right\}\). Tìm giá trị của a sao cho \({C_U}A = \left\{ 1 \right\}\).
Cho \(A = \left\{ { - 2; - 1;0;1;2} \right\},B = \left\{ {x\left| {x + 1 \le 0} \right.} \right\}\). Tập hợp \(A\backslash B\) bằng:
A. \(\left\{ {0;1;2} \right\}\)
B. \(\left\{ { - 1} \right\}\)
C. \(\left\{ { - 2; - 1} \right\}\)
D. \(\left\{ { - 2} \right\}\)
Cho các tập hợp \(A = \left\{ { - 1;0;1;2} \right\},B = \left\{ {x\left| {x - 1 \ge 0} \right.} \right\}\). Tập hợp \(A\backslash B\) bằng:
A. \(\left\{ 2 \right\}\)
B. \(\left\{ { - 1;0;1} \right\}\)
C. \(\left\{ {1;2} \right\}\)
D. \(\left\{ { - 1;0} \right\}\)
Cho các tập hợp \(A = \{ 0;2;4;6;8\} \) và \(B = \{ 1;2;3;4;5;6\} \). Tìm \(A\backslash B\).
-
A.
{0;8}
-
B.
{1;3;5}
-
C.
{0;2;8}
-
D.
{2;4;6}
Tập hợp \(C = (2; + \infty ){\rm{\backslash }}[ - 3;8]\) bằng tập hợp nào sau đây?
-
A.
\((8; + \infty )\)
-
B.
\((2;8]\)
-
C.
\([ - 3;2)\)
-
D.
\([ - 3; + \infty )\)







Danh sách bình luận